Équations de la ligne -

Vous trouverez ici les formules de tous les types d’équations de la droite. De plus, vous pourrez voir des exemples de la façon dont ils sont calculés et, en plus, pratiquer avec des exercices résolus des équations de la ligne.

Quelles sont toutes les équations de la droite ?

Rappelez-vous que la définition mathématique d’une ligne est un ensemble de points consécutifs qui sont représentés dans la même direction sans courbes ni angles.

Ainsi, pour exprimer analytiquement toute droite dans le plan (dans R2) on utilise les équations de la droite, et pour les trouver il suffit d’un point appartenant à la droite et du vecteur directeur de ladite droite. Avec seulement ces deux éléments géométriques, vous pouvez trouver absolument toutes les différentes équations de la ligne, qui sont les suivantes :

Les équations de la droite sont l’équation vectorielle, les équations paramétriques, l’équation continue, l’équation implicite (ou générale), l’équation explicite, l’équation point-pente et l’équation canonique (ou segmentaire).

Tous les types d’équations de ligne ont le même objectif : représenter mathématiquement une ligne. Mais chaque équation de la droite a ses propriétés et donc, selon le problème, il vaut mieux utiliser l’une ou l’autre.

Une fois que nous avons vu le concept des équations de la droite, nous passons maintenant à l’analyse des caractéristiques de chaque type d’équation de la droite en particulier. Ci-dessous, vous avez une explication détaillée des différents types d’équations de la ligne, mais si vous le souhaitez, vous pouvez aller directement à la fin du tableau récapitulatif avec les formules de toutes les équations de la ligne .

Équation vectorielle de la droite

Ouais

$\vv{\text{v}}$ est le vecteur directeur de la droite et $P$ un point qui appartient à la droite :

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

La formule de l’équation vectorielle de la droite est :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2) \end{empheq}$

Où:

$x$ et $y$ sont les coordonnées cartésiennes de tout point de la ligne.
$P_1$ et $P_2$ sont les coordonnées d’un point connu faisant partie de la ligne $P(P}_1,P_2).$
$\text{v}_1$ et $\text{v}_2$ sont les composantes du vecteur directeur de la droite $\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$ est un scalaire (un nombre réel) dont la valeur dépend de chaque point de la droite.

C’est l’équation vectorielle de la droite dans le plan, c’est-à-dire lorsque l’on travaille avec des points et des vecteurs de 2 coordonnées (dans R2). Cependant, si nous faisions des calculs dans l’espace (en R3), nous devrions ajouter un composant supplémentaire à l’équation de la droite :

$(x,y,z)=(P_1,P_2,P_3)+t\cdot (\text{v}_1,\text{v}_2,\text{v}_3)$

Équations paramétriques de la ligne

Les équations paramétriques d’une ligne peuvent être obtenues à partir de son équation vectorielle :

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

On multiplie d’abord le paramètre

$t$ par le vecteur directeur de la droite :

$(x,y)=(P_1,P_2)+ (t\cdot\text{v}_1,t\cdot\text{v}_2)$

Ensuite, nous ajoutons les coordonnées X et Y :

$(x,y)=(P_1+t\cdot\text{v}_1,P_2+t\cdot\text{v}_2)$

Et, enfin, en effaçant chaque variable séparément, nous obtenons les équations paramétriques de la ligne :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases} \end{empheq}$

Où:

$x$ et $y$ sont les coordonnées cartésiennes de tout point de la ligne.
$P_1$ et $P_2$ sont les coordonnées d’un point connu faisant partie de la ligne $P(P}_1,P_2).$
$\text{v}_1$ et $\text{v}_2$ sont les composantes du vecteur directeur de la droite $\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$ est un scalaire (un nombre réel) dont la valeur dépend de chaque point de la droite.

Comme précédemment, ce sont les équations paramétriques de la droite dans le plan (dans R2), mais pour trouver les équations paramétriques de la droite dans l’espace (dans R3) il faudrait ajouter une équation de plus pour la troisième variable Z :

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}$

Equation continue de la droite

L’équation continue de toute droite peut être déduite de ses équations paramétriques :

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

Si nous effaçons le paramètre

$t$ à partir de chaque équation paramétrique on obtient les expressions suivantes :

$t =\cfrac{x-P_1}{\text{v}_1}}$

$t =\cfrac{y-P_2}{\text{v}_2}}$

E En égalant les deux équations résultantes, nous obtenons l’équation continue de la droite :

$t= t$

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

En bref, l’ équation continue de la droite est :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2} \end{empheq}$

Où:

$x$ et $y$ sont les coordonnées cartésiennes de tout point de la ligne.
$P_1$ et $P_2$ sont les coordonnées d’un point connu faisant partie de la ligne $P(P}_1,P_2).$
$\text{v}_1$ et $\text{v}_2$ sont les composantes du vecteur directeur de la droite $\vv{\text{v}}=(\text{v}_1,\text{v}_2).$

Cette formule est pour l’équation continue de la droite quand on travaille en 2 dimensions (en 2D). Mais si nous effectuions des opérations en 3 dimensions (3D), nous devrions ajouter un composant supplémentaire à l’équation de la ligne :

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}= \cfrac{z-P_3}{\text{v}_3}$

Équation implicite ou générale de la droite

Ouais

$\vv{\text{v}}$ est le vecteur directeur de la droite et $P$ un point qui appartient à la droite :

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

La formule de l’ équation implicite, générale ou cartésienne de la droite est :

Où:

$x$ et $y$ sont les coordonnées cartésiennes de tout point de la ligne.
le coefficient $A$ est la seconde composante du vecteur directeur de la droite : $A=\text{v}_2}$
le coefficient $B$ est la première composante du vecteur de direction changé de signe : $B=-\text{v}_1}$
le coefficient $C$ est calculé en remplaçant le point connu $P$ dans l’équation de la droite.

Outre la formule, l’équation implicite d’une droite peut également être obtenue en multipliant les fractions de l’équation continue.

Équation explicite de la droite

La formule de l’ équation explicite de la droite est :

Où:

$m$ est la pente de la droite.
$n$ son ordonnée à l’origine, c’est-à-dire la hauteur à laquelle elle coupe l’axe Y.

Dans la section ci-dessous, vous verrez comment les paramètres sont déterminés

$m$ et $n$ de la ligne droite Mais, en particulier, une autre façon de trouver l’équation explicite consiste à utiliser l’équation implicite ; pour cela, l’inconnu doit être résolu $y$ de l’équation implicite.

Signification des paramètres m et n

Comme nous l’avons vu dans la définition de l’équation explicite de la droite, le paramètre

$m$ est la pente de la droite et $n$ son ordonnée à l’origine. Mais qu’est ce que ça veut dire? Voyons cela à partir de la représentation graphique d’une ligne :

Quelle est l'équation explicite de la droite y=mx+b

Le terme indépendant

$\bm{n}$ est le point d’intersection de la droite avec l’axe des ordonnées (axe OY). Par exemple, dans le graphique ci-dessus $n$ est égal à 1 car la droite coupe l’axe des y en y=1.

D’autre part, le terme

$\bm{m}$ indique la pente de la droite , c’est-à-dire son inclinaison. Comme vous le voyez sur le graphique, $m$ est égal à 2 puisque la droite s’élève de 2 unités verticales pour 1 unité horizontale.

Évidemment, si la pente est positive la fonction est croissante (monte), par contre si la pente est négative la fonction est décroissante (descend).

Calculer la pente d’une droite

Une fois que nous savons exactement quelle est la pente d’une droite, voyons comment elle est calculée. Ainsi, il existe 3 manières différentes de déterminer numériquement la pente d’une droite :

Étant donné deux points différents sur la ligne $P_1(x_1,y_1)$ et $P_2(x_2,y_2),$ La pente de la droite est égale à :

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Ouais $\vv{\text{v}}= (\text{v}_1,\text{v}_2)$ est le vecteur directeur de la droite, sa pente vaut :

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Ouais $\alpha$ est l’angle que forme la droite avec l’axe des abscisses (axe X), la pente de la droite est équivalente à la tangente dudit angle :

$m = \text{tg}(\alpha )$

formule de l'équation explicite de la droite

Équation point-pente de la ligne

La formule de l’ équation point-pente de la droite est la suivante :

Où:

$m$ est la pente de la droite.
$P_1, P_2$ sont les coordonnées d’un point sur la droite $P(P_1,P_2).$

Equation canonique ou segmentaire de la droite

Bien que cette variante de l’équation de la droite soit moins connue, l’équation canonique de la droite peut être obtenue à partir des points d’intersection de la droite avec les axes cartésiens.

Soit les deux points d’intersection avec les axes d’une droite donnée :

Couper avec l’axe X :

$(a,0)$

Couper avec l’axe Y :

$(0,b)$

La formule de l’équation canonique de la droite est :

En mathématiques, l’équation canonique de la droite est aussi appelée équation segmentaire ou équation symétrique.

En revanche, les coefficients

$a$ et $b$ On peut aussi les trouver à partir de l’équation générale de la droite par les formules suivantes :

$Ax+By+C=0$

$a = -\cfrac{C}{A} \qquad \qquad b = -\cfrac{C}{B}$

Toutes les équations de la droite (formules)

En résumé, voici un tableau qui reprend les formules de toutes les équations de la droite :

Exemple de calcul des équations de la droite

Maintenant que nous avons vu toute l’explication de l’équation de la droite, voyons comment un problème typique des équations de la droite est résolu :

Trouver toutes les équations de la droite déterminée par le point $P$ et le vecteur $\vv{\text{v}}.$

$P(3,-1) \qquad \qquad \vv{\text{v}}=(2,4)$

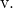
Tout d’abord, on retrouve l’équation vectorielle de la droite à partir de sa formule :

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

Il suffit de substituer les coordonnées du point et du vecteur dans la formule :

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(3,-1)+t\cdot (2,4)} \quad \vphantom{\Bigl(}}$

Dans un second temps, on retrouve les équations paramétriques de la droite à travers sa formule correspondante :

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Et nous déterminons également l’équation continue de la droite avec sa formule :

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-3}{2}=\cfrac{y-(-1)}{4}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x-3}}{\bm{2}}\bm{=}\cfrac{\bm{y+1}}{\bm{4}}\quad \vphantom{\Biggl(}}$

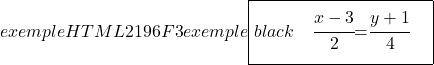
Comme vous l’avez vu, les équations vectorielles, paramétriques et continues sont faciles à calculer, il vous suffit d’utiliser leurs formules respectives.

Passons maintenant à la recherche de l’équation générale (ou implicite) de la droite. Pour ce faire, on croise les deux fractions de l’équation continue :

$4\cdot (x-3)= 2 \cdot (y+1)$

$4x-12= 2y+2$

$4x-12-2y-2=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{4x-2y-14=0}\quad \vphantom{\Bigl(}}$

Maintenant, nous pouvons déterminer l’équation explicite de la ligne résolvant pour l’inconnu

$y$ de l’équation implicite :

$4x-2y-14=0$

$-2y=-4x+14$

$y=\cfrac{-4x+14}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=2x-7}\quad \vphantom{\Bigl(}}$

Par conséquent, la pente de la droite est égale à 2 (terme qui accompagne la variable indépendante

$x$ ).

$m=2$

Et avec cela, nous pouvons calculer l’équation point-pente de la ligne avec sa formule :

$y-P_2=m(x-P_1)$

$y-(-1)=2(x-3)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y+1=2(x-3)}\quad \vphantom{\Bigl(}}$

Enfin, pour trouver l’équation segmentaire de la droite on calcule ses points d’intersection avec les axes OX et OY puis on applique sa formule :

$y=2x-7$

Point d’intersection avec l’axe des abscisses (axe X)

$y=0$

$0=2x-7$

$-2x=-7$

$x=\cfrac{-7}{-2} = \cfrac{7}{2}$

$\displaystyle \left(\frac{7}{2}, 0\right)$

Point d’intersection avec l’axe des ordonnées (axe Y)

$x=0$

$y=2\cdot 0-7$

$y=-7$

$\displaystyle \left(0,-7\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\frac{\bm{7}}{\bm{2}}}+\cfrac{\bm{y}}{\bm{-7}} \bm{= 1} \quad \vphantom{\Biggl(}}$

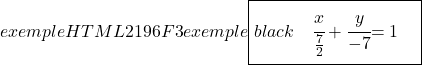
équation de droite passant par deux points

Un autre problème très courant des équations de la droite est de trouver l’équation de la droite qui est déterminée par deux points donnés. Bien que nous puissions calculer le vecteur directeur de la ligne avec les 2 points puis l’équation, nous vous fournissons ci-dessous une formule avec laquelle vous pouvez trouver directement et facilement l’équation de ladite ligne.

Soit deux points situés sur une droite :

$P_1(x_1,y_1) \qquad \qquad P_2(x_2,y_2)$

La formule pour trouver l’équation de la droite à partir de ses 2 points est :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1) \end{empheq}$

Cette formule permet de calculer directement l’équation point-pente de la droite lorsqu’on nous donne 2 points par lesquels passe la droite.

Problèmes résolus des équations de la droite

Exercice 1

Trouvez l’équation vectorielle, les équations paramétriques et l’équation continue de la ligne définie par le point

$P$ et son vecteur directeur $\vv{\text{v}}.$ Être à la fois :

$P(0,3) \qquad \qquad \vv{\text{v}}=(-1,5)$

voir solution

Tout d’abord, nous calculons l’équation vectorielle de la ligne à partir de sa formule :

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(0,3)+t\cdot (-1,5)} \quad \vphantom{\Bigl(}}$

On retrouve ensuite les équations paramétriques de la droite grâce à sa formule correspondante :

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Et, enfin, nous déterminons l’équation continue de la droite avec sa formule respective :

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-0}{-1}=\cfrac{y-3}{5}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x}}{\bm{-1}}\bm{=}\cfrac{\bm{y-3}}{\bm{5}}\quad \vphantom{\Biggl(}}$

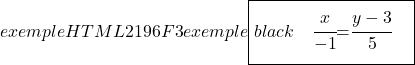
Exercice 2

Trouvez l’équation implicite, l’équation explicite et l’équation point-pente de la ligne déterminée par le point

$P$ et son vecteur directeur est $\vv{\text{v}}.$

$P(-4,3) \qquad \qquad \vv{\text{v}}=(2,6)$

voir solution

La formule de l’équation implicite de la droite est :

$Ax+By+C=0$

Il faut donc trouver les coefficients A, B et C. Les inconnues A et B s’obtiennent à partir des coordonnées du vecteur directeur de la droite, car l’égalité suivante est toujours vérifiée :

$\vv{\text{v}}= (-B,A)$

Par conséquent, le coefficient A est la seconde coordonnée du vecteur, et le coefficient B est la première coordonnée du vecteur changé de signe :

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}$

Par conséquent, nous n’avons qu’à trouver le coefficient C. Pour ce faire, nous devons substituer le point dont nous savons qu’il appartient à la droite dans son équation :

$P(-4,3)$

$6x-2y+C=0 \ \xrightarrow{x=-4 \ ; \ y=3} \ 6\cdot (-4)-2\cdot 3+C=0$

$-24-6+C=0$

$-30+C=0$

$C=30$

Donc l’équation implicite, générale ou cartésienne de la droite est :

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x-2y+30=0}\quad \vphantom{\Bigl(}}$

Maintenant, nous pouvons déterminer l’équation explicite de la ligne résolvant pour l’inconnu

$y$ de l’équation implicite :

$6x-2y+30=0$

$-2y=-6x-30$

$y=\cfrac{-6x-30}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=3x+15}\quad \vphantom{\Bigl(}}$

Par conséquent, la pente de la droite est égale à 3 (terme avant la variable indépendante

$x$ ).

$m=3$

Et, à partir de la valeur de la pente de la droite, on peut calculer l’équation point-pente de la droite avec sa formule :

$y-P_2=m(x-P_1)$

$y-3=3(x-(-4))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-3=3(x+4)}\quad \vphantom{\Bigl(}}$

Exercice 3

Déterminez 3 points sur la droite suivante, exprimée sous forme d’équation implicite ou générale :

$4x+2y-8 = 0$

voir solution

Pour calculer un point sur une ligne, nous devons simplement attribuer une valeur à l’une des variables, puis trouver la valeur de l’autre variable à ce point.

On calcule un premier point en faisant

$x=0:$

$4\cdot 0+2y-8 = 0$

$2y = 8$

$y = \cfrac{8}{2}$

$y = 4$

$\bm{P_1(0,4)}$

On trouve alors un deuxième point donnant une autre valeur à la variable

$x,$ par exemple $x=1:$

$4\cdot 1+2y-8 = 0$

$2y = 8-4$

$2y = 4$

$y = \cfrac{4}{2}$

$y = 2$

$\bm{P_2(1,2)}$

Et, pour finir, on calcule un troisième point en résolvant

$x=2:$

$4\cdot 2+2y-8 = 0$

$2y = 8-8$

$2y = 0$

$y = \cfrac{0}{2}$

$y = 0$

$\bm{P_3(2,0)}$

Exercice 4

Trouver toutes les équations de la droite définie par le point

$P$ et le vecteur $\vv{\text{v}}.$

$P(-1,4) \qquad \qquad \vv{\text{v}}=(-3,6)$

voir solution

Tout d’abord, on retrouve l’équation vectorielle de la droite à partir de sa formule :

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(-1,4)+t\cdot (-3,6)} \quad \vphantom{\Bigl(}}$

Dans un second temps, on retrouve les équations paramétriques de la droite à travers sa formule correspondante :

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Et nous déterminons également l’équation continue de la droite à l’aide de sa formule :

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-(-1)}{-3}=\cfrac{y-4}{6}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x+1}}{\bm{-3}}\bm{=}\cfrac{\bm{y-4}}{\bm{6}}\quad \vphantom{\Biggl(}}$

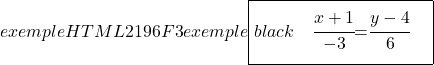
Passons maintenant à la recherche de l’équation implicite ou générale de la droite. Pour ce faire, on croise les deux fractions de l’équation continue :

$6\cdot (x+1)= -3 \cdot (y-4)$

$6x+6= -3y+12$

$6x+6+3y-12=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x+3y-6=0}\quad \vphantom{\Bigl(}}$

Maintenant, nous pouvons déterminer l’équation explicite de la ligne résolvant pour l’inconnu

$y$ de l’équation implicite :

$6x+3y-6=0$

$3y=-6x+6$

$y=\cfrac{-6x+6}{3}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=-2x+2}\quad \vphantom{\Bigl(}}$

Par conséquent, la pente de la droite est équivalente à -2 (terme qui accompagne la variable indépendante

$x$ ).

$m=-2$

Et avec cela, nous pouvons calculer l’équation point-pente de la ligne avec sa formule :

$y-P_2=m(x-P_1)$

$y-4=-2(x-(-1))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-4=-2(x+1)}\quad \vphantom{\Bigl(}}$

Enfin, pour trouver l’équation segmentaire de la droite, on calcule les points d’intersection de la droite avec les axes OX et OY puis on utilise sa formule :

$y=-2x+2$

Point d’intersection avec l’axe des abscisses (axe X)

$y=0$

$0=-2x+2$

$2x=2$

$x=\cfrac{2}{2} =1$

$\displaystyle \left(1, 0\right)$

Point d’intersection avec l’axe des ordonnées (axe Y)

$x=0$

$y=-2\cdot 0+2$

$y=2$

$\displaystyle \left(0,2\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\bm{1}}+\cfrac{\bm{y}}{\bm{2}} \bm{= 1} \quad \vphantom{\Biggl(}}$

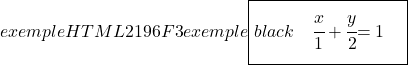
Exercice 5

Trouver l’équation de la droite qui passe par les deux points suivants :

$P_1 (4,-1) \qquad \qquad P_2(5,2)$

voir solution

Puisque nous connaissons déjà deux points de la droite, nous appliquons directement la formule de l’équation de la droite à 2 points donnés :

$y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1)$

Maintenant, nous substituons les coordonnées cartésiennes des points dans la formule :

$y-(-1)= \cfrac{2-(-1)}{5-4} (x-4)$

Et, enfin, nous calculons la pente de la droite :

$y+1= \cfrac{3}{1} (x-4)$

$y+1= 3(x-4)$

L’équation de la droite qui passe par ces deux points est donc :

$\bm{y+1= 3(x-4)}$

Quelles sont toutes les équations de la droite ?

Équation vectorielle de la droite

Équations paramétriques de la ligne

Equation continue de la droite

Équation implicite ou générale de la droite

Équation explicite de la droite

Signification des paramètres m et n

Calculer la pente d’une droite

Équation point-pente de la ligne

Equation canonique ou segmentaire de la droite

Toutes les équations de la droite (formules)

Exemple de calcul des équations de la droite

équation de droite passant par deux points

Problèmes résolus des équations de la droite

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Leave a Comment Cancel Reply