Point d'équation – pente de la ligne

Sur cette page, vous trouverez la formule de l’équation point-pente de la ligne et, également, les différentes façons qui existent pour la calculer. De plus, vous pourrez voir plusieurs exemples et pratiquer avec des exercices résolus étape par étape.

Formule de l’équation point-pente de la ligne

L’équation point-pente d’une droite est une façon d’exprimer mathématiquement une droite. En particulier, vous n’avez besoin que de la pente et des coordonnées d’un point sur la droite pour trouver l’équation point-pente d’une droite.

La formule de l’équation point-pente de la droite est la suivante :

$y-y_0=m(x-x_0)$

Où

$m$ est la pente de la droite et $x_0, y_0$ sont les coordonnées d’un point sur la droite $P(x_0,y_0).$

Voyons comment l’équation point-pente de la ligne est calculée à l’aide d’un exemple :

Ecrire l’équation point-pente de la droite qui passe par le point 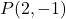$P(2,-1)$ et de pente m=3.

La formule de l’équation point-pente de la droite est la suivante :

$y-y_0=m(x-x_0)$

Dans ce cas, l’énoncé nous dit que la pente de la droite est m=3, donc l’équation de la droite sera la suivante :

$y-y_0=3(x-x_0)$

De plus, on sait aussi que la droite passe par le point

$P(2,-1)$ , il faut donc substituer les coordonnées de ce point dans l’équation :

$P(2,-1)$

$y-y_0=3(x-x_0) \ \xrightarrow{x_0=2 \ ; \ y_0=-1} \ y-(-1)=3(x-2)$

L’équation point-pente de la droite est donc :

$\bm{y+1=3(x-2)}$

Gardez à l’esprit qu’en dehors de l’équation point-pente, il existe d’autres façons d’exprimer analytiquement une ligne : l’équation vectorielle, les équations paramétriques, l’équation continue, l’équation implicite (ou générale) et l’équation explicite d’une ligne. Si vous êtes plus intéressé, vous pouvez vérifier en quoi consiste chacun d’eux sur notre site Web.

Que signifie la pente d’une droite ?

Comme nous l’avons vu dans la définition de l’équation point-pente d’une droite, le paramètre

$m$ est la pente de la droite. Mais vraiment… que signifie la pente d’une droite ? Voyons cela à partir de la représentation graphique d’une ligne :

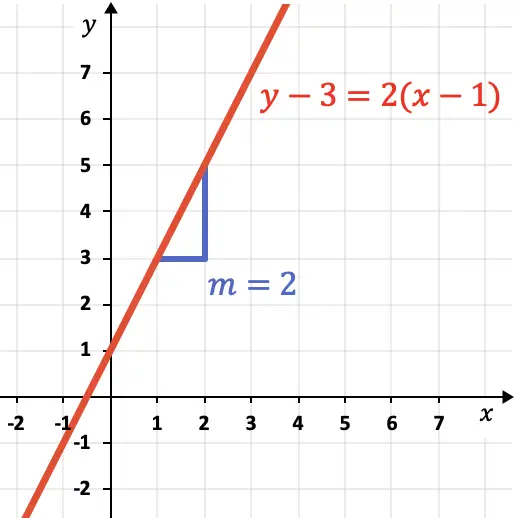
Quelle est l'équation point-pente d'une droite ?

La pente de la ligne indique sa raideur. Comme vous pouvez le voir sur la ligne du graphique,

$m$ est égal à 2 puisque la droite s’élève de 2 unités verticales pour 1 unité horizontale.

Évidemment, si la pente est positive la fonction est croissante (monte), par contre si la pente est négative la fonction est décroissante (descend).

Comment calculer la pente d’une droite

Par ailleurs, il existe 3 manières différentes de déterminer numériquement la pente d’une droite :

Étant donné deux points différents sur la ligne $P_1(x_1,y_1)$ et $P_2(x_2,y_2),$ La pente de la droite est égale à :

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Ouais $\vv{\text{v}}= (\text{v}_1,\text{v}_2)$ est le vecteur directeur de la droite, sa pente vaut :

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Ouais $\alpha$ est l’angle que forme la droite avec l’axe des abscisses (axe X), la pente de la droite est équivalente à la tangente dudit angle :

$m = \text{tg}(\alpha )$

formule de l'équation explicite de la droite

Position relative des lignes

Enfin, la pente d’une droite sert aussi à connaître la relation entre plusieurs droites. Puisque deux droites parallèles ont même pente et, d’autre part, si la pente d’une droite est l’inverse négatif de la pente d’une autre droite, cela signifie que ces deux droites sont perpendiculaires .

Calculer l’équation point-pente de la droite qui passe par deux points

Un problème très courant consiste à déterminer l’équation point-pente à partir de deux points appartenant à la droite. Voyons comment il est résolu à travers un exemple:

Trouvez l’équation point-pente de la droite qui passe par les deux points suivants :

$P_1(5,2) \qquad P_2(3,6)$

Pour trouver l’équation point-pente de la droite, nous devons déterminer quelle est la pente de la droite. Nous calculons donc la pente de la ligne en utilisant la formule du côlon :

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{6-2}{3-5} = \cfrac{4}{-2}= -2$

Ainsi, l’équation point-pente de la droite sera la suivante :

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Par conséquent, nous n’avons qu’à substituer les coordonnées cartésiennes d’un point sur la ligne dans l’équation :

$P_1(5,2)$

$y-y_0=-2(x-x_0) \ \xrightarrow{x_0=5 \ ; \ y_0=2} \ y-2=-2(x-5)$

$\bm{y-2=-2(x-5)}$

C’est bien aussi si on met l’autre point de l’énoncé dans l’équation de la droite :

$P_1(3,6)$

$y-6=-2(x-3)$

Trouver l’équation point-pente d’une droite à partir du graphique

Comme nous l’avons vu dans les sections ci-dessus, il existe plusieurs façons de trouver numériquement l’équation point-pente d’une ligne. Cependant, il peut également être trouvé graphiquement. Voyons comment cela se fait à travers un exemple :

Déterminez l’équation point-pente de la ligne représentée dans le graphique suivant :

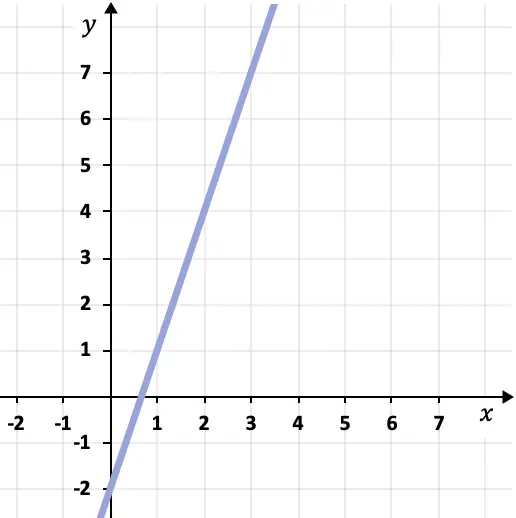
Pour déterminer l’équation point-pente de la ligne tracée, nous devons trouver sa pente et un point sur la ligne.

Dans ce cas, la pente de la droite est égale à 3, car la droite s’élève de 3 unités verticales pour chaque unité horizontale.

$m = 3$

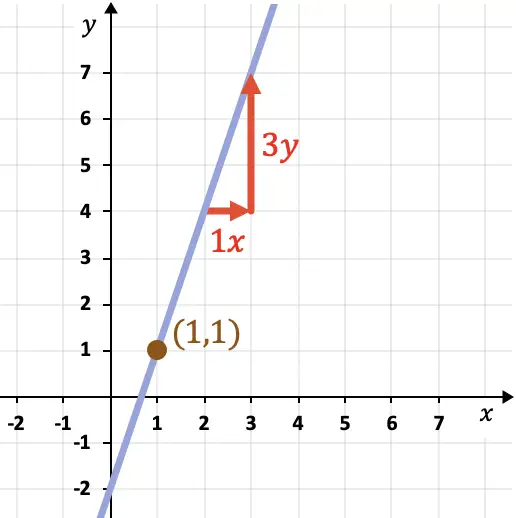
Ensuite, nous avons besoin d’un point sur la ligne. Pour ce faire, on peut choisir n’importe quel point du graphe par lequel passe la droite, par exemple le point (1,1).

$P(1,1)$

Par conséquent, nous pouvons maintenant trouver l’équation point-pente de la ligne en appliquant sa formule :

$y-y_0=m(x-x_0)$

$y-1=3(x-1)$

déterminer graphiquement la pente du point d'équation d'une ligne

Problèmes résolus de l’équation point-pente de la ligne

Exercice 1

Ecrire l’équation point-pente de la droite qui passe par le point

$P(1,4)$ et sa pente est $m=-2.$

voir solution

La formule de l’équation point-pente de la ligne est :

$y-y_0=m(x-x_0)$

Dans ce cas, l’énoncé nous dit que la pente de la droite est m=-2, donc l’équation de la droite sera la suivante :

$y-y_0=-2(x-x_0)$

De plus, nous savons également par l’énoncé que la droite passe par le point

$P(1,4)$ , il suffit donc de substituer les coordonnées du point dans l’équation de la droite :

$P(1,4)$

$\bm{y-4=-2(x-1)}$

Exercice 2

Quelle est l’équation point-pente de la droite qui passe par les deux points suivants ?

$P_1(1,6) \qquad P_2(4,0)$

voir solution

Pour trouver l’équation point-pente de la droite, nous devons déterminer quelle est la pente de la droite. On calcule donc la pente de la droite avec sa formule :

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{0-6}{4-1} = \cfrac{-6}{3}= -2$

Ainsi, l’équation point-pente de la droite sera la suivante :

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Par conséquent, nous n’avons qu’à substituer les coordonnées d’un point sur la droite dans l’équation :

$P_1(1,6)$

$\bm{y-6=-2(x-1)}$

Il aurait également été correct de mettre l’autre point de l’énoncé dans l’équation :

$y=-2(x-4)$

Exercice 3

Trouvez l’équation point-pente de la droite qui passe par les deux points suivants :

$P_1(1,-2) \qquad P_2(2,3)$

voir solution

Pour trouver l’équation point-pente de la droite, il faut d’abord calculer sa pente :

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{3-(-2)}{2-1} = \cfrac{3+2}{1}=\cfrac{5}{1}= 5$

Ainsi, l’équation point-pente de la droite sera la suivante :

$y-y_0=m(x-x_0)$

$y-y_0=5(x-x_0)$

Par conséquent, nous n’avons qu’à substituer les coordonnées d’un point sur la droite dans l’équation :

$P_1(1,-2)$

$y-(-2)=5(x-1)$

$\bm{y+2=5(x-1)}$

Il est également correct de mettre l’autre point de l’énoncé dans l’équation de la droite :

$y-3=5(x-2)$

Exercice 4

Calculez l’équation point-pente de la droite qui forme un angle de 45º avec l’axe X et passe par l’origine des coordonnées.

voir solution

Si la droite fait un angle de 45 degrés avec l’axe OX, sa pente sera :

$m = \text{tg}(45º) = 1$

$y-y_0=1(x-x_0)$

$y-y_0=x-x_0$

Et une fois que nous connaissons la pente de la droite, nous pouvons trouver l’équation point-pente en substituant un point sur la droite dans l’équation. De plus, l’énoncé nous dit que la ligne passe par l’origine des coordonnées, ce qui signifie qu’elle passe par le point (0,0). Pourtant:

$P(0,0)$

$y-y_0=x-x_0 \ \xrightarrow{x=0 \ ; \ y=0} \ y-0=x-0$

L’équation point-pente de la droite est donc :

$\bm{y=x}$

Exercice 5

Trouver l’équation de la pente ponctuelle de la droite parallèle à la droite

$r$ et ce qui se passe à travers le point $P(-1,-3).$ être hétéro $r:$

$r: \; y-1=2(x+5)$

voir solution

La pente de la ligne

$r$ est égal à 2 (chiffre avant les parenthèses), et pour que deux droites soient parallèles, il faut qu’elles aient la même pente, donc :

$m = 2$

$y-y_0=2(x-x_0)$

Et une fois que nous connaissons la pente de la droite, il suffit de substituer les coordonnées d’un point qui appartient à la droite dans la formule :

$P(-1,-3)$

$y-(-1)=2(x-(-3))$

L’équation point-pente de la droite est donc :

$\bm{y+1=2(x+3)}$

Exercice 6

Déterminez l’équation point-pente de chaque droite représentée dans le graphique suivant :

équation explicite de la ligne exercice résolu étape par étape

voir solution

bleu droit

La droite bleue augmente d’un Y pour chaque X, donc sa pente est égale à 1. Par contre, elle passe par le point (2,4), donc :

$y-4 =x-2$

vert droit

La ligne verte augmente de trois Y pour chaque X, donc sa pente est de 3. De plus, l’un de ses points est (2,2), donc :

$y-2 =3(x-2)$

ligne rouge

La ligne rouge diminue de deux Y pour chaque X, donc sa pente est égale à -2. Et le point (0,-2) appartient à cette droite, donc :

$y =-2(x+2)$

Point d’équation – pente de la ligne

Formule de l’équation point-pente de la ligne

Que signifie la pente d’une droite ?

Comment calculer la pente d’une droite

Position relative des lignes

Calculer l’équation point-pente de la droite qui passe par deux points

Trouver l’équation point-pente d’une droite à partir du graphique

Problèmes résolus de l’équation point-pente de la ligne

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Leave a Comment Cancel Reply