Équation implicite, générale ou cartésienne du plan

Explication de la façon dont l’équation implicite du plan (formule), également connue sous le nom d’équation générale ou cartésienne, est calculée. De plus, vous trouverez comment trouver l’équation du plan à partir de son vecteur normal. Et, en plus, vous pourrez voir des exemples et des exercices résolus étape par étape.

Quelle est l’équation implicite ou générale du plan ?

En géométrie analytique, l’ équation implicite d’un plan , aussi appelée équation générale ou cartésienne du plan, est une équation qui permet d’exprimer mathématiquement n’importe quel plan. Pour trouver l’équation implicite ou générale d’un plan, nous avons besoin d’un point et de deux vecteurs linéairement indépendants appartenant à ce plan.

Formule de l’équation implicite ou générale du plan

Soit un point et deux vecteurs directeurs d’un plan :

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

L’équation implicite, générale ou cartésienne d’un plan s’obtient en résolvant le déterminant suivant et en fixant le résultat égal à 0 :

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Ainsi, l’ équation implicite ou générale du plan résultant sera la suivante :

$Ax+By+Cz+D=0$

Il est important que les deux vecteurs de la formule soient linéairement indépendants l’un de l’autre, c’est-à-dire qu’ils doivent avoir une direction différente. Et pour que cette condition soit remplie il suffit que les deux vecteurs ne soient pas parallèles.

équation implicite ou générale ou cartésienne du pan xy dans r3

Bien qu’il ne soit pas nécessaire de connaître la raison de cette formule, vous pouvez voir sa démonstration ci-dessous.

Partant des équations paramétriques d’un plan, nous allons passer à l’équation implicite (ou générale) du plan :

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Tout d’abord, nous passons le terme indépendant de chaque équation paramétrique à l’autre côté de l’équation :

$\displaystyle \begin{cases}x-P_x= \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y-P_y = \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z-P_z = \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Ou équivalent:

$\displaystyle \begin{cases} \lambda \text{u}_x + \mu \text{v}_x =x-P_x\\[1.7ex] \lambda \text{u}_y + \mu \text{v}_y=y-P_y \\[1.7ex] \lambda\text{u}_z + \mu \text{v}_z =z-P_z\end{cases}$

Pour que le système d’équations ci-dessus ait une solution réalisable, le rang de la matrice suivante doit être égal à 2 (théorème de Rouché-Frobenius) :

$\displaystyle\begin{pmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z\end{pmatrix}$

Donc si la plage de la matrice précédente doit être deux, le déterminant 3×3 doit nécessairement être égal à zéro :

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Et en résolvant ce déterminant, on obtient l’équation générale, implicite ou cartésienne d’un plan :

$Ax+By+Cz+D=0$

Ainsi, nous venons de voir l’équation implicite (ou générale) et les équations paramétriques du plan, cependant, il existe encore plus de façons d’exprimer analytiquement un plan, comme l’équation vectorielle et l’équation canonique. Vous pouvez voir la formule et l’explication de toutes les équations du plan dans ce lien.

Exemple de comment trouver l’équation implicite ou générale du plan

Voyons comment déterminer l’équation implicite (ou générale ou cartésienne) d’un plan à travers un exemple :

Trouver l’équation implicite ou générale du plan qui passe par le point 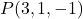$P(3,1,-1)$ et contient les vecteurs 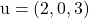$\vv{\text{u}}=(2,0,3)$ et $\vv{\text{v}}=(4,-1,2).$

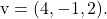
Pour calculer l’équation générale ou implicite du plan, il faut résoudre le déterminant suivant formé par les deux vecteurs, les variables et les coordonnées du point :

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Donc, nous substituons les vecteurs et le point dans la formule :

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z-(-1) \end{vmatrix} =0$

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z+1 \end{vmatrix} =0$

Et maintenant on résout le déterminant d’ordre 3, par exemple avec la règle de Sarrus ou par cofacteurs (ou adjoints) :

$-2(z+1)+12(y-1)+3(x-3)-4(y-1) = 0$

Maintenant, nous opérons et regroupons les termes :

$3(x-3)+8(y-1) -2(z+1) = 0$

$3x-9+8y-8 -2z-2 = 0$

$3x+8y-2z-19 = 0$

Par conséquent, l’équation implicite ou générale du plan est :

$\bm{3x+8y-2z-19 = 0}$

Calculer l’équation implicite ou générale d’un plan à partir de son vecteur normal

Un problème très typique des équations d’un plan est de trouver à quoi ressemble l’équation d’un plan donné à partir d’un point et de son vecteur normal (ou perpendiculaire). Alors, voyons comment ça marche.

Mais il faut d’abord savoir que les composantes X, Y, Z du vecteur normal à un plan coïncident respectivement avec les coefficients A, B, C de l’équation implicite (ou générale) dudit plan.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Où

$\vv{n}$ est le vecteur orthogonal au plan $\pi.$

Une fois que nous connaissons la relation précédente, voyons un exemple de résolution de ce type de problèmes d’équations planes :

Déterminer l’équation implicite ou générale du plan qui passe par le point 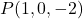$P(1,0,-2)$ et l’un de ses vecteurs normaux est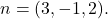 $\vv{n}=(3,-1,2) .$

La formule de l’équation implicite, générale ou cartésienne d’un plan est :

$Ax+By+Cz+D=0$

Ainsi, à partir du vecteur normal, on peut trouver les coefficients A, B et C car ils sont équivalents aux composantes de son vecteur normal :

$\vv{n}=(3,-1,2) \ \longrightarrow \ 3x-1y+2z+D=0$

Alors que nous n’avons qu’à trouver le paramètre D. Pour ce faire, nous substituons les coordonnées du point qui appartient au plan dans l’équation :

$P(1,0,-2)$

$3\cdot 1-0+2\cdot (-2)+D=0$

$3-4+D=0$

$-1+D=0$

$D=1$

Donc l’équation implicite ou générale du plan est :

$\bm{3x-y+2z+1 = 0}$

Problèmes résolus de l’équation implicite ou générale du plan

Exercice 1

Trouver l’équation implicite ou générale du plan qui passe par le point

$P(-2,1,3)$ et contient les vecteurs $\vv{\text{u}}=(4,1,3)$ et $\vv{\text{v}}=(5,3,-1).$

voir solution

Pour calculer l’équation générale ou implicite du plan, il faut résoudre le déterminant suivant formé par les deux vecteurs, les trois variables et les coordonnées du point :

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Donc, nous substituons les vecteurs et le point dans la formule :

$\displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0$

Et maintenant on résout le déterminant de la matrice 3×3 avec la méthode de votre choix :

$12(z+1)+15(y-1)+1(x+2)-9(x+2)-4(y-1)-5(z+1) = 0$

Enfin, nous effectuons les opérations et regroupons les termes similaires :

$-8(x+2)+11(y-1)+7(z+1) = 0$

$-8x-16+11y-11+7z+7=0$

$-8x+11y+7z-20= 0$

Donc l’équation implicite ou générale du plan est :

$\bm{-8x+11y+7z-20 = 0}$

Exercice 2

Déterminez si le point

$P(-1,5,-3)$ appartient au plan suivant :

$\pi : \ 2x+y+6z-5=0$

voir solution

Pour que le point soit dans le plan, il faut vérifier son équation. Par conséquent, nous devons substituer les coordonnées cartésiennes du point dans l’équation du plan et vérifier si l’équation est remplie :

$2x+y+6z-5=0$

$P(-1,5,-3)$

$2\cdot (-1)+5+6\cdot (-3)-5=0$

$-2+5-18-5=0$

$-20\neq 0$

Le point ne respecte pas l’équation du plan, il ne fait donc pas partie de ce plan.

Exercice 3

Trouvez l’équation implicite (ou générale) du plan qui contient les trois points suivants :

$A(5,-1,-2) \qquad B(2,1,3) \qquad C(4,1,-2)$

voir solution

Pour trouver l’équation implicite du plan, nous devons trouver deux vecteurs linéairement indépendants qui se trouvent dans le plan. Et, pour cela, on peut calculer deux vecteurs qui sont définis par les 3 points :

$\vv{AB} = B - A = (2,1,3) - (5,-1,-2) = (-3,2,5)$

$\vv{AC} = C - A = (4,1,-2) - (5,-1,-2) = (-1,2,0)$

Les coordonnées des deux vecteurs trouvés ne sont pas proportionnelles, elles sont donc effectivement linéairement indépendantes l’une de l’autre.

Maintenant nous connaissons déjà deux vecteurs directeurs et un point du plan, de sorte que nous pouvons déjà appliquer la formule de l’équation générale du plan :

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Nous substituons les vecteurs et l’un des trois points dans la formule :

$\displaystyle\begin{vmatrix}-3 & -1 & x-5 \\[1.1ex]2 & 2 & y+1 \\[1.1ex]5& 0 & z+2 \end{vmatrix} =0$

Et, enfin, on résout le déterminant :

$-6(z+2)-5(y+1)-10(x-5)+2(z+2)=0$

$-10(x-5)-5(y+1)-4(z+2)=0$

$-10x+50-5y-5-4z-8=0$

$-10x-5y-4z+37=0$

En bref, l’équation implicite, générale ou cartésienne du plan en question est :

$\bm{-10x-5y-4z+37=0}$

Exercice 4

Calcule l’équation implicite ou générale du plan dans l’espace qui passe par le point

$P(3,4,-3)$ et l’un de ses vecteurs normaux est $\vv{n}=(5,-2,-3) .$

voir solution

La formule de l’équation implicite, générale ou cartésienne d’un plan est :

$Ax+By+Cz+D=0$

Eh bien, à partir du vecteur normal, nous pouvons trouver les coefficients A, B et C, car ils sont respectivement égaux aux composantes du vecteur normal :

$\vv{n}=(5,-2,-3) \ \longrightarrow \ 5x-2y-3z+D=0$

Pour que nous ayons seulement besoin de trouver le paramètre D. Pour ce faire, nous substituons les coordonnées du point qui appartient au plan dans l’équation :

$P(3,4,-3)$

$5\cdot 3-2\cdot 4-3\cdot (-3)+D=0$