Équation de la ligne tangente -

Dans cet article, nous verrons comment trouver l’équation de la tangente à une courbe. De plus, vous pouvez vous entraîner avec des exercices résolus de différents niveaux de difficulté.

Équation de la ligne tangente à une fonction en un point

L’ équation de la tangente à la fonction f(x) au point x=x ₀ est :

$y -y_0= m(x-x_0)$

Où le point P(x ₀ ,y ₀ ) est le point où la tangente et la fonction coïncident. Et la pente de la tangente, m, est égale à la dérivée de la courbe au point x ₀ , c’est-à-dire m=f'(x ₀ ).

Dans l’image ci-dessus, vous pouvez voir une courbe

$f(x)$ représenté en bleu et une ligne orange tangente à la fonction $f(x)$ Sur le point $x=x_0$ , puisqu’ils n’ont que ce point commun. Eh bien, l’équation de cette tangente est $y -y_0= m(x-x_0)$ , et sa pente est $m=f'(x_0)$ .

Comment trouver l’équation de la tangente

Pour trouver l’équation de la tangente à une fonction en un point, vous devez faire :

Trouvez la pente de la ligne tangente en calculant la dérivée de la fonction au point de tangence.
Déterminez un point sur la ligne tangente.
Trouvez l’équation de la ligne tangente en utilisant la pente calculée et le point de la ligne tangente.

Exemple de l’équation de la tangente à une courbe

Une fois que nous avons vu la théorie sur l’équation de la tangente, voyons comment calculer l’équation d’une tangente en résolvant un exemple étape par étape :

Calculer l’équation de la tangente à la courbe 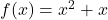$f(x)=x^2+x$ Sur le point $x=1$ .

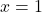On sait que l’équation de la tangente est toujours de la forme suivante :

$y -y_0= m(x-x_0)$

La première chose à faire est de calculer la pente de la droite. Ainsi, la pente de la tangente,

$m$ , sera la valeur de la dérivée de la courbe au point de tangence x=1, soit $m=f'(1).$ On différencie donc la fonction puis on calcule $f'(1):$

$f(x)=x^2+x \quad \longrightarrow \quad f'(x)=2x+1$

$f'(1)= 2\cdot 1+1=2+1=3$

$m=f'(1)=3$

Une fois que nous connaissons la valeur de

$m$ , nous devons trouver un point $(x_0,y_0)$ de la ligne tangente pour compléter l’équation de la ligne tangente.

L’ équation de la tangente et la courbe ont toujours un point commun , qui dans ce cas est

$x=1$ . Par conséquent, comme la courbe $f(x)$ passe par ce point, on peut trouver l’autre composante du point en calculant $f(1):$

$f(x)=x^2+x$

$f(1)=1^2+1=2$

Le point de tangence est donc :

$P(1,2)$

La courbe et la tangente passent par ce point, nous pouvons donc également l’utiliser pour trouver l’équation de la tangente.

Il ne reste plus qu’à substituer les valeurs trouvées de la pente et du point de la tangente dans son équation :

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)$

En bref, l’équation de la tangente est :

$\bm{y-2=3(x-1)}$

Vous pouvez également exprimer l’équation de la droite tangente avec l’équation explicite de la droite :

$\bm{y=3x-1}$

Ci-dessous vous pouvez voir la courbe représentée

$f(x)=x^2+x$ et sa ligne tangente à $x=1,$ $y-2=3(x-1):$

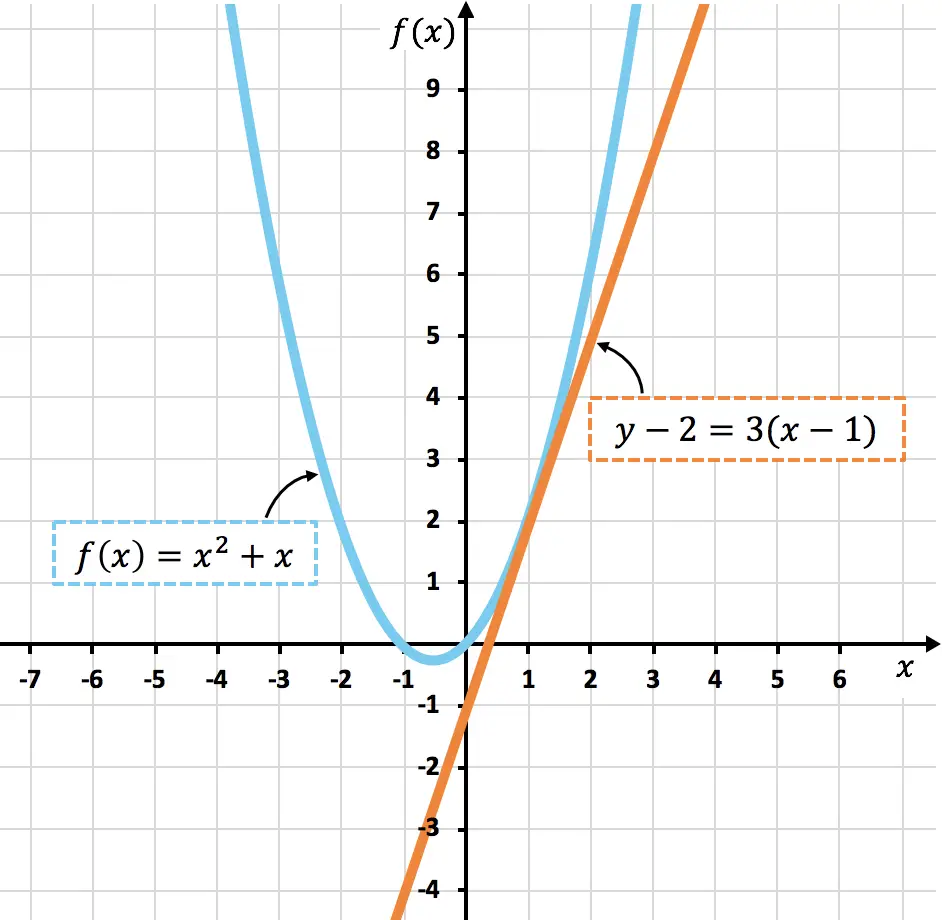
équation de la ligne tangente à une courbe en un point

Comme vous pouvez le constater, la courbe

$f(x)=x^2+x$ et la tangente $y-2=3(x-1)$ ils n’ont en commun que le point $(1,2)$ , exactement comme nous l’avions calculé.

Exercices résolus sur l’équation de la tangente

Exercice 1

Calculer l’équation de la tangente à la courbe

$f(x)=2x^2-4x+3$ Sur le point $x=2 .$

Voir la solution

L’équation de la tangente sera toujours de la forme suivante :

$y-y_0=m(x-x_0)$

Étape 1 : Calculer la pente de la ligne tangente

La pente, m , est la valeur de la dérivée de la courbe au point de tangence. Par conséquent, dans ce cas

$m = f'(2):$

$f(x)=2x^2-4x+3 \ \longrightarrow \ f'(x)= 4x-4$

$f'(2)= 4\cdot 2-4=8-4=4$

$m=f'(2)=4$

Étape 2 : Trouver un point sur la ligne tangente

L’équation de la tangente et la courbe ont toujours un point commun, qui dans ce cas est

$x=2$ . Par conséquent, comme la courbe $f(x)$ passe par ce point, on peut trouver l’autre composante du point en calculant $f(2):$

$f(x)=2x^2-4x+3$

$f(2)=2\cdot 2^2-4\cdot 2+3 =2 \cdot 4 -8 +3 = 3$

Ainsi, le point par lequel passent à la fois la courbe et la tangente est le point

$(2,3).$

Étape 3 : Écrivez l’équation de la tangente

Il ne reste plus qu’à substituer les valeurs trouvées de la pente et du point de la tangente dans son équation :

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)$

L’équation de la tangente est donc :

$\bm{y -3= 4(x-2)}$

Exercice 2

Calculer l’équation de la tangente à la courbe

$\displaystyle f(x)=-3x^2+2x$ à l’origine des coordonnées.

Voir la solution

L’origine des coordonnées fait référence au point

$(0,0).$ Il faut donc calculer la tangente à la fonction au point $(0,0) .$

Tout d’abord, on détermine la valeur de la pente de la tangente en calculant la dérivée à l’origine des coordonnées :

$f(x)=-3x^2+2x \ \longrightarrow \ f'(x)= -6x+2$

$f'(0)= -6\cdot 0+2=2$

$m=f'(0)=2$

Dans ce cas, nous connaissons déjà un point par lequel passe la tangente. Parce que l’énoncé nous dit que la droite doit être tangente à la courbe à l’origine des coordonnées, c’est-à-dire au point

$(0,0).$

Donc le point que partagent la courbe et la tangente est le point

$(0,0).$

Enfin, il suffit de substituer dans son équation les valeurs trouvées pour la pente et le point de la tangente :

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)$

En conclusion, l’équation de la tangente est :

$y -0= 2(x-0)$

$\bm{y = 2x}$

Exercice 3

Calculer la ligne tangente à la courbe

$f(x)=x^2-2x-1$ qui est parallèle à la droite $y-4x-6=0$ .

Voir la solution

Dans ce problème, on nous dit que la tangente doit être parallèle à la droite

$y-4x-6=0 .$ Et deux droites sont parallèles si elles ont la même pente. La tangente doit donc avoir la même pente que la droite $y-4x-6=0.$

Cela signifie qu’il faut trouver la pente de la droite

$y-4x-6=0 .$ Pour ce faire, nous effaçons la variable et :

$y-4x-6=0 \ \longrightarrow \ y =4x+6$

Donc la pente de la droite

$y=4x+5$ est 4, puisque la pente d’une droite est le nombre qui multiplie le x lorsque le y est clair.

Par conséquent, la pente de la tangente doit également être de 4, car pour qu’elles soient parallèles, elles doivent avoir la même pente.

$m=4$

Dans ce cas ils ne nous indiquent pas le point de tangence entre la courbe et la tangente. Mais on sait que la dérivée de la courbe au point de tangence est égale à la pente de la tangente, c’est-à-dire

$m=f'(x_0)$ . Eh bien, comment pouvons-nous connaître la valeur de $m$ , nous pouvons trouver x ₀ à partir de l’équation $m=f'(x_0):$

Pour ce faire, on calcule d’abord la dérivée de

$f(x):$

$f(x)= x^2-2x-1 \ \longrightarrow \ f'(x)=2x-2$

Et maintenant nous résolvons

$m=f'(x_0)$ sachant que $m = 4 :$

$m =f'(x_0)$

$4 =2(x_0)-2$

$4+2 =2x_0$

$6 =2x_0$

$\cfrac{6}{2} =x_0$

$3=x_0$

Et une fois qu’on connaît la coordonnée x du point, on peut trouver l’autre coordonnée du point en calculant

$f(3):$

$f(3)=3^2-2\cdot 3-1= 9-6-1=2$

Ainsi, le point par lequel passent à la fois la courbe et la tangente est le point

$(3,2).$

Il ne reste plus qu’à substituer les valeurs trouvées de la pente et du point de la tangente dans son équation :

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)$

Et l’équation de la tangente est :

$\bm{y -2=4(x-3)}$

Exercice 4

Calculer la ligne tangente à la courbe

$f(x)=2x^2+5x+1$ qui forme un angle de 45º avec l’axe X.

Voir la solution

L’énoncé du problème nous dit que la ligne tangente doit former un angle de 45º avec l’axe X. Dans ces cas, la formule suivante doit être appliquée pour trouver la valeur de la pente :

$m = \text{tg}\left(\alpha\right)$

$m = \text{tg}\left(45^{\text{o}}\right) = 1$

L’énoncé ne précise pas le point de tangence entre la courbe et la ligne tangente. Mais on sait que la dérivée de la courbe au point de tangence est équivalente à la pente de la tangente, c’est-à-dire

$m=f'(x_0)$ . On peut donc calculer x ₀ en résolvant l’équation $m=f'(x_0):$

Pour ce faire, on calcule d’abord la dérivée de

$f(x):$

$f(x)=2x^2+5x+1\ \longrightarrow \ f'(x)=4x+5$