Vous trouverez ici comment l’équation de l’ellipse (formule) est calculée, qu’elle ait l’origine comme centre ou non. Vous trouverez également quels sont les éléments de l’ellipse, comment les calculer et à quoi ils servent. De plus, vous pourrez voir des exemples et des exercices résolus d’équations d’ellipses.
Formule d’équation d’ellipse
La formule de l’ équation de l’ellipse en coordonnées cartésiennes est la suivante :
![]()
Où:
 et
et sont les coordonnées du centre de l’ellipse :
sont les coordonnées du centre de l’ellipse :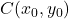
 est le rayon horizontal de l’ellipse.
est le rayon horizontal de l’ellipse. est le rayon vertical de l’ellipse.
est le rayon vertical de l’ellipse.
Équation de l’ellipse centrée à l’origine
Un type d’ellipse très courant est celui dont le centre est à l’origine des coordonnées, c’est-à-dire au point (0,0). C’est pourquoi nous allons voir comment trouver l’équation de l’ellipse centrée à l’origine.
En suivant la formule de l’équation de l’ellipse :
![]()
Si l’ellipse est centrée sur l’origine des coordonnées, cela signifie que
![]() et
et![]() sont égaux à 0, donc votre équation sera :
sont égaux à 0, donc votre équation sera :
![]()
Il y a des mathématiciens qui appellent aussi cette expression l’équation canonique ou équation réduite de l’ellipse.
éléments de l’ellipse
Une fois que nous aurons vu à quoi ressemble l’équation de l’ellipse, nous allons voir quels sont ses éléments. Mais d’abord, rappelons ce qu’est exactement une ellipse :
L’ellipse est une ligne plate, fermée et incurvée très semblable à la circonférence, mais sa forme est plus ovale. En particulier, l’ellipse est le lieu de tous les points d’un plan dont la somme des distances à deux autres points fixes (appelés foyers F et F’) est constante.
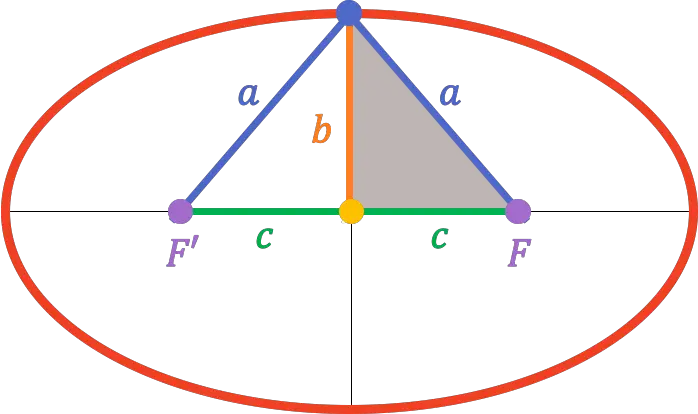
Ainsi, les éléments d’une ellipse sont :
- Les foyers : ce sont les points fixes F et F’ (points de couleur violette dans l’image ci-dessous). La somme des distances entre n’importe quel point de l’ellipse et chaque foyer est constante pour tous les points de l’ellipse.
- Axe principal ou focal : c’est l’axe de symétrie de l’ellipse dans laquelle se situent les foyers. Aussi appelé grand axe.
- Axe secondaire : c’est l’axe de symétrie de l’ellipse perpendiculaire à l’axe principal. Il est aussi appelé petit axe et correspond à la bissectrice perpendiculaire du segment qui rejoint les foyers.
- Centre : est le point d’intersection des axes de l’ellipse. De plus, c’est le centre de symétrie de l’ellipse (point orange sur le graphique).
- Sommets : points d’intersection de l’ellipse avec ses axes de symétrie (points noirs).
- Demi-grand axe ou axe principal : segment qui va du centre de l’ellipse aux sommets de l’axe principal.
- Demi-petit axe ou axe secondaire : segment compris entre le centre de l’ellipse et les sommets de l’axe secondaire.
- Distance focale : C’est la distance entre les deux foyers.
- Distance semi-focale : correspond à la distance entre le centre et chacun des foyers.
- Les vecteurs radio : sont les segments qui joignent n’importe quel point de l’ellipse à chaque foyer (segments bleus dans le graphique).

Relation entre les éléments d’une ellipse
Les différents éléments d’une ellipse sont liés les uns aux autres. De plus, les relations entre eux sont très importantes pour les exercices sur les ellipses, car elles sont généralement nécessaires pour résoudre des problèmes sur les ellipses et déterminer leurs équations.
Comme nous l’avons vu plus haut dans la définition de l’ellipse, la distance d’un point quelconque de l’ellipse au foyer F plus la distance du même point au foyer F’ est constante. Eh bien, cette valeur constante est égale à deux fois ce que mesure le demi-grand axe. Autrement dit, l’égalité suivante vaut pour tout point d’une ellipse :
![]()
Où
![]() et
et![]() est la distance du point P au foyer F et F’ respectivement et
est la distance du point P au foyer F et F’ respectivement et![]() est la longueur de l’axe semi-focal.
est la longueur de l’axe semi-focal.
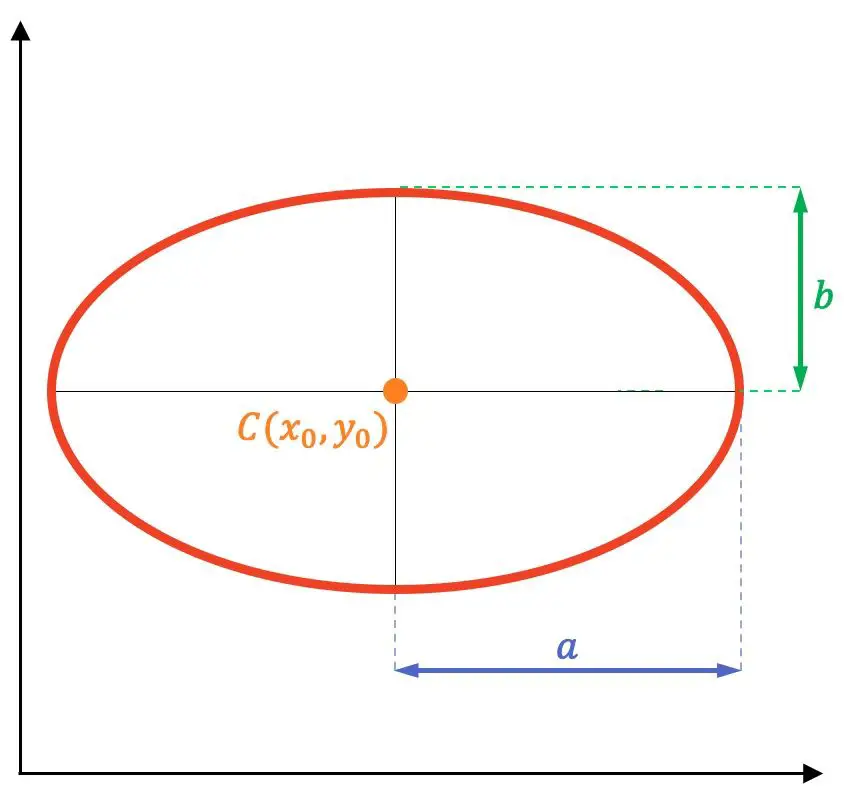
Par conséquent, puisque le sommet de l’axe secondaire est juste au milieu de l’axe focal, la distance de celui-ci à l’un des foyers est équivalente à la longueur de l’axe semi-principal (
![]() ):
):
Ainsi, à partir du théorème de Pythagore , il est possible de trouver la relation qui existe entre le demi-axe principal, le demi-axe secondaire et la demi-distance focale :
![]()
Retenez cette formule car elle vous sera très utile pour calculer le résultat des exercices avec des ellipses.
Excentricité d’ellipse
Évidemment, toutes les ellipses ne sont pas identiques, mais certaines sont plus allongées et d’autres plus aplaties. Ainsi, il existe un coefficient qui est utilisé pour mesurer à quel point une ellipse donnée est arrondie. Ce coefficient est appelé excentricité et est calculé avec la formule suivante :
![]()
Où
![]() est la distance du centre de l’ellipse à l’un de ses foyers et
est la distance du centre de l’ellipse à l’un de ses foyers et![]() la longueur du demi-grand axe.
la longueur du demi-grand axe.
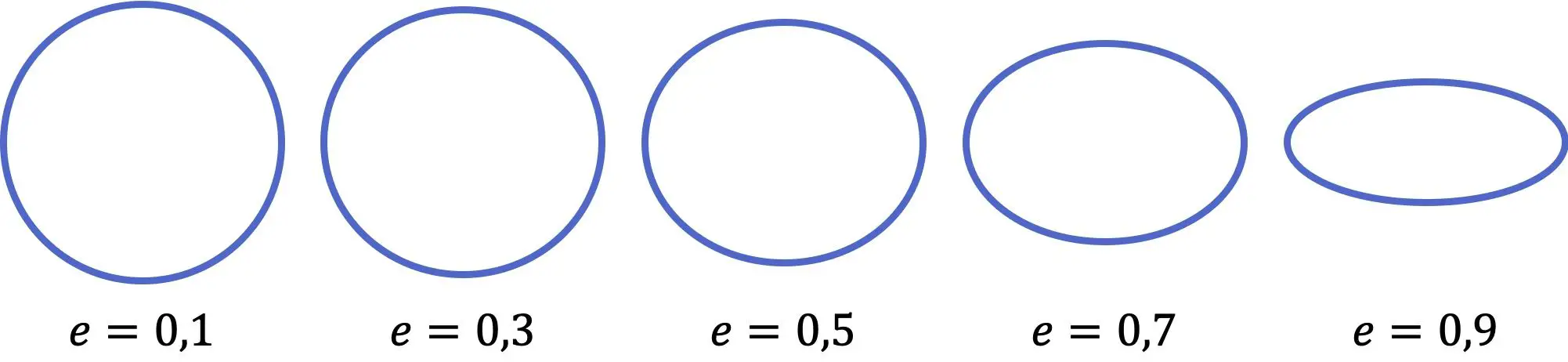
Comme vous pouvez le voir dans la représentation précédente, plus la valeur de l’excentricité de l’ellipse est petite, plus elle ressemble à un cercle, par contre, plus le coefficient est grand, plus l’ellipse est aplatie. De plus, la valeur d’excentricité va de zéro (cercle parfait) à un (ligne horizontale), tous deux non inclus.
 a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{5^2-4^2}=\sqrt{9} = 3
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{5^2-4^2}=\sqrt{9} = 3 ![]() \cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2}+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\bm{(y+1)^2}}{\bm{9}} \bm{= 1}
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2}+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\bm{(y+1)^2}}{\bm{9}} \bm{= 1} \cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1![]() \cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}}{\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}
\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}}{\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1} a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{13^2-5^2}=\sqrt{144} = 12
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{13^2-5^2}=\sqrt{144} = 12 ![]() \cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2}+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}}{\bm{144}} \bm{= 1}
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2}+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}}{\bm{144}} \bm{= 1} d_h=10-(-4) =14 a =\cfrac{14}{2} = 7
d_h=10-(-4) =14 a =\cfrac{14}{2} = 7 ![]() d_v=6-(-4) =10 b =\cfrac{10}{2} = 5
d_v=6-(-4) =10 b =\cfrac{10}{2} = 5 ![]() C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{2} = 1 C(3,1)
C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{2} = 1 C(3,1) ![]() \cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2}+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{(y-1)^2}}{\bm{25}} \bm{= 1}
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2}+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{(y-1)^2}}{\bm{25}} \bm{= 1}![]() a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt{24}
a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt{24} ![]() \sqrt{24}
\sqrt{24}![]() C(3,1) \bm{F\left(3+\sqrt{24},1}\right)} \bm{F\left(3-\sqrt{24},1}\right)}
C(3,1) \bm{F\left(3+\sqrt{24},1}\right)} \bm{F\left(3-\sqrt{24},1}\right)}  2c = 6 c=\cfrac{6}{2} c=3
2c = 6 c=\cfrac{6}{2} c=3 ![]() d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a
d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a ![]() a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt{7}
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt{7} ![]() \cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2}+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2}+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$
Enfin, si cet article vous a été utile, vous serez sûrement aussi intéressé par nos pages sur la formule de l’hyperbole et la formule de la parabole . Vous y trouverez une explication détaillée de ce que sont l’hyperbole et la parabole, leurs équations, leurs caractéristiques, des exemples, des exercices résolus,…