Équation canonique, segmentaire ou symétrique de la droite

Vous trouverez ici l’explication de ce qu’est la formule de l’équation canonique (ou segmentaire) de la droite, aussi appelée équation symétrique. De plus, vous pourrez voir des exemples et pratiquer avec des exercices résolus. Et, même, vous trouverez comment l’équation canonique est calculée à partir de l’équation générale (ou implicite) de la droite.

Quelle est l’équation canonique ou segmentaire de la droite ?

Rappelez-vous que la définition mathématique d’une ligne est un ensemble de points consécutifs qui sont représentés dans la même direction sans courbes ni angles.

Ainsi, l’ équation canonique de la droite , également appelée équation segmentaire de la droite , est une manière d’exprimer mathématiquement n’importe quelle droite. Pour ce faire, il suffit de connaître les points d’intersection avec les axes de coordonnées de ladite ligne.

D’autre part, en géométrie analytique, l’équation canonique (ou segmentaire) de la droite est aussi appelée équation symétrique de la droite .

Formule de l’équation canonique ou segmentaire de la droite

L’équation canonique ou segmentaire de la droite est l’expression algébrique de la droite qui peut être déterminée en connaissant les valeurs où la droite coupe l’axe des abscisses et l’axe des ordonnées.

Si une droite coupe les axes cartésiens aux points suivants :

Point d’intersection avec l’axe X :

$(a,0)$

Point d’intersection avec l’axe Y :

$(0,b)$

La formule de l’équation canonique (ou segmentaire) de la droite est :

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

équation canonique segmentaire ou symétrique de la ligne dans l'espace

Il est à noter qu’il n’y a pas d’équation canonique (ou segmentaire) de la droite dans aucun des trois cas suivants :

Lorsque la ligne est verticale, c’est-à-dire parallèle à l’axe OY. Parce que l’équation d’une ligne verticale est $x=k.$
Lorsque la ligne est horizontale, c’est-à-dire parallèle à l’axe OX. Parce que l’équation d’une ligne horizontale est $y=k.$
Lorsque la ligne passe par l’origine des coordonnées (point 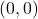$(0,0)$ ), puisque nous aurions alors deux indéterminations dans l’équation de la droite.

Exemple de comment trouver l’équation canonique ou segmentaire de la droite

Afin que vous compreniez mieux le concept, nous allons résoudre un problème d’équation segmentaire (ou canonique) de la droite :

Trouvez l’équation canonique ou segmentaire de la droite qui passe par les deux points suivants :

$A(0,4) \qquad \qquad B(-2,0)$

Dans ce cas, la déclaration ne nous donne pas 2 points, mais plutôt les deux points d’intersection avec les axes.

Point d’intersection de la droite avec l’axe X :

$(-2,0)$

Point d’intersection de la droite avec l’axe Y :

$(0,4)$

Donc, puisque nous connaissons déjà les deux points d’intersection avec les axes, il suffit d’appliquer la formule de l’équation canonique ou segmentaire de la droite :

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

Et enfin, nous substituons la valeur des paramètres

$a$ et $b$ dans la formule :

$\cfrac{\bm{x}}{\bm{-2}}\bm{+} \cfrac{\bm{y}}{\bm{4}}\bm{= 1}$

Vous savez maintenant quelle est l’équation canonique (ou segmentaire) de la droite. Cependant, vous devez savoir qu’il existe d’autres façons d’exprimer une ligne, et parmi elles, l’ équation explicite se démarque. Ce type d’équation de ligne est difficile à comprendre pleinement, nous avons donc tout expliqué en détail à ce sujet sur la page liée.

Calculer l’équation canonique ou segmentaire de la droite à partir de son équation générale

Nous venons de voir un moyen de déterminer l’équation canonique ou segmentaire de la droite, mais il existe aussi d’autres méthodes :

L’équation canonique ou segmentaire d’une droite peut être obtenue à partir de l’ équation générale (ou implicite) de cette même droite :

$Ax+By+C=0$

Tout d’abord, nous changeons de côté au coefficient C :

$Ax+By=-C$

Ensuite, nous divisons l’équation entière par la valeur du paramètre C changé de signe :

$\cfrac{Ax+By}{-C}=\cfrac{-C}{-C}$

$\cfrac{Ax}{-C}+\cfrac{By}{-C}=1$

Et, par les propriétés des fractions, on arrive à la formule de l’équation canonique ou segmentaire de la droite :

$\cfrac{x}{-\frac{C}{A}}+\cfrac{y}{-\frac{C}{B}}=1$

Il résulte donc de cette formule que les termes

$a$ et $b$ de l’équation canonique d’une droite sont équivalentes aux expressions suivantes :

$a= -\cfrac{C}{A} \qquad \qquad b= -\cfrac{C}{B}$

Problèmes résolus de l’équation canonique ou segmentaire de la droite

Exercice 1

Quels sont les points d’intersection avec les axes de coordonnées de la droite suivante ?

$\cfrac{x}{3}+ \cfrac{y}{-1}= 1$

voir solution

La droite de l’exercice s’exprime sous la forme d’une équation canonique ou segmentaire de la droite, dont la formule est :

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

Par conséquent, les points où la ligne coupe les axes de coordonnées sont :

Point d’intersection avec l’axe X :

$\bm{(3,0)}$

Point d’intersection avec l’axe Y :

$\bm{(0,-1)}$

Exercice 2

Quelle est l’équation canonique ou segmentaire de la droite représentée graphiquement ?

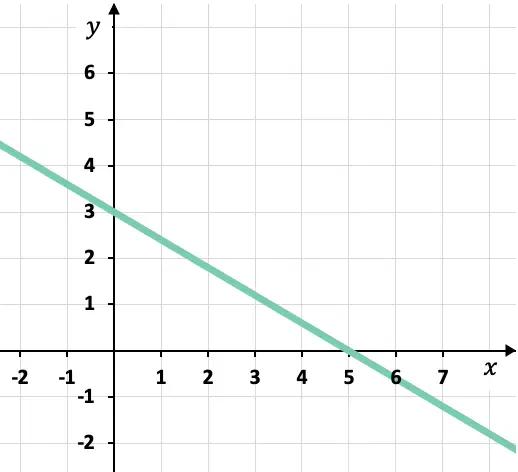
équation canonique segmentaire ou symétrique dans le plan

voir solution

À partir du graphique, nous pouvons connaître les points où la ligne croise les axes de coordonnées :

Point d’intersection de la droite avec l’axe X :

$(5,0)$

Point d’intersection de la droite avec l’axe Y :

$(0,3)$

Donc, une fois que l’on connaît déjà les 2 points d’intersection avec les axes, il suffit d’utiliser la formule de l’équation canonique ou segmentaire de la droite :

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

Et enfin, nous substituons la valeur des paramètres

$a$ et $b$ dans la formule :

$\cfrac{\bm{x}}{\bm{5}}\bm{+} \cfrac{\bm{y}}{\bm{3}}\bm{= 1}$

Exercice 3

Calculez l’équation canonique ou segmentaire de la droite déterminée par l’équation générale (ou implicite) suivante :

$3x-2y+6=0$

voir solution

Pour passer d’une équation générale à une équation segmentaire, il faut d’abord isoler le terme indépendant de l’équation :

$3x-2y+6=0$

$3x-2y=-6$

Deuxièmement, nous divisons l’équation entière par le coefficient du côté droit de l’équation :

$\cfrac{3x-2y}{-6}=\cfrac{-6}{-6}$

$\cfrac{3x}{-6}+\cfrac{-2y}{-6}=\cfrac{-6}{-6}$

L’expression ci-dessus est équivalente à la suivante :

$\cfrac{x}{\frac{-6}{3}}+\cfrac{y}{\frac{-6}{-2}}=1$

De sorte que l’équation canonique, segmentaire ou symétrique de la droite est :

$\cfrac{\bm{x}}{\bm{-2}}\bm{+} \cfrac{\bm{y}}{\bm{3}}\bm{= 1}$

Exercice 4

Déterminer l’équation canonique ou segmentaire dont le vecteur directeur est

$\vv{\text{v}}=(4,-3)$ et passe par le point $P(-1,5).$

voir solution

On trouve d’abord facilement l’équation continue de la droite à partir de son vecteur directeur et d’un point qui appartient à la droite :

$\cfrac{x-P_1}{\text{v}_1} = \cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-(-1)}{4} = \cfrac{y-5}{-3}$

$\cfrac{x+1}{4} = \cfrac{y-5}{-3}$

Calculons maintenant l’équation générale de la droite en multipliant les fractions en croix et en regroupant les termes résultants :

$-3(x+1) = 4(y-5)$

$-3x-3 = 4y-20$

$-3x-3 - 4y+20 =0$

$-3x - 4y+17 =0$

Il suffit donc de convertir l’équation générale de la droite en une équation canonique. Pour ce faire, nous effaçons d’abord le terme indépendant de l’équation :

$-3x - 4y=-17$