Vous trouverez ici comment la distance d’une ligne à un plan est calculée et, en plus, vous pourrez voir des exemples et des exercices résolus étape par étape.
Quelle est la distance entre une ligne et un avion ?
En géométrie analytique, la distance entre une droite et un plan dans l’espace dépend de la position relative entre ces deux éléments géométriques :
- Si la droite est incluse dans le plan ou si la droite et le plan sont parallèles , la distance qui les sépare est nulle.
- Si la ligne est parallèle au plan , la distance de la ligne au plan est trouvée en prenant n’importe quel point sur la ligne et en calculant la distance de ce point au plan.
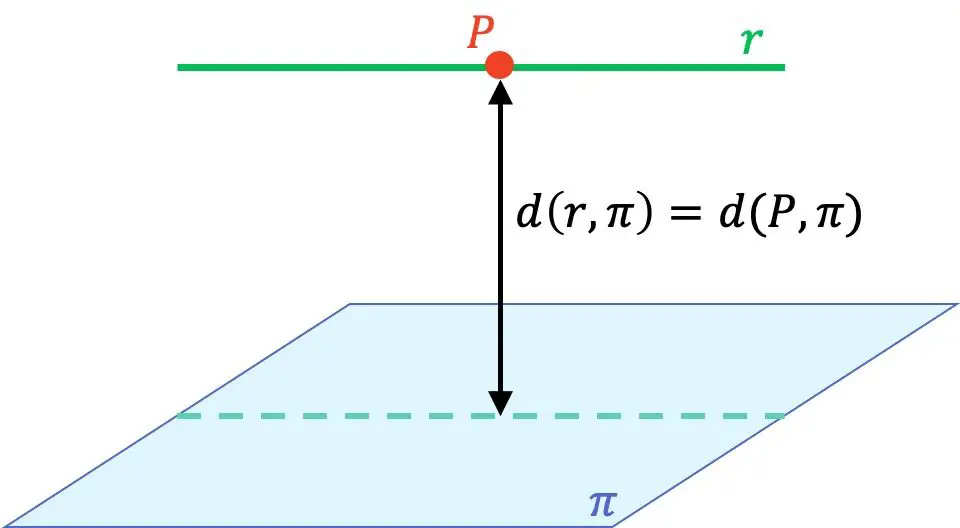
Par conséquent, pour calculer la distance d’une ligne à un plan, il est essentiel que vous sachiez déterminer la position relative entre une ligne et un plan et comment calculer la distance entre un point et un plan . Alors si vous n’êtes pas tout à fait clair ou si vous ne connaissez pas les formules, nous vous recommandons de jeter d’abord un œil aux pages liées, où vous trouverez des explications, des exemples et des exercices résolus étape par étape.
Exemple de calcul de la distance entre une droite et un plan
Pour que vous puissiez voir comment trouver la distance entre une droite et un plan dans l’espace (en R3), nous allons résoudre un problème à titre d’exemple :
- Quelle est la distance de la ligne
 à l’avion
à l’avion ?
?
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=-2+t \\[1.7ex] y=1-3t \\[1.7ex] z=-1+2t\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4785f2386b4ff9387b56cf8c5645c62d_l3.png)
![]()
Pour trouver la distance entre la droite et le plan, il faut d’abord connaître la position relative entre les deux.
D’une part, la droite est définie sous forme d’équations paramétriques, donc son vecteur directeur et un point par lequel elle passe sont :
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(1,-3,2) \\[2ex] P(-2,1,-1) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0765b71f9eead3b644fd5de150cdf321_l3.png)
Et, d’autre part, le vecteur normal au plan est :
![]()
Ainsi, pour déterminer la position relative entre le plan et la droite, il faut calculer le produit scalaire entre le vecteur directeur de la droite et le vecteur normal au plan :
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (1,-3,2) \cdot (4,2,1) \\[2ex] & = 1 \cdot 4-3 \cdot 2 +2\cdot 1 \\[2ex] &= 4 -6 +2 \\[2ex] & = 0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-39d2d450c32a6fdf3182a3d16cc18116_l3.png)
Le résultat du produit scalaire est égal à zéro, de sorte que la ligne ne peut être contenue que dans le plan ou lui être parallèle. Donc, pour savoir de quel cas il s’agit, on substitue les coordonnées cartésiennes du point de la droite dans l’équation du plan :
![]()
![]()
![]()
En substituant le point de la droite dans l’équation du plan on obtient une inégalité, donc le point ne respecte pas l’équation du plan et, par conséquent, la droite et le plan sont parallèles.
Une fois que nous savons que la ligne et le plan sont parallèles, nous pouvons maintenant calculer la distance géométrique entre eux. Pour ce faire, nous prenons le point sur la ligne et calculons la distance de ce point au plan.
![]()
Donc, nous utilisons la formule pour la distance d’un point à un plan :
![]()
Maintenant, nous substituons la valeur de chaque inconnue dans la formule :
![]()
Et, enfin, on fait les opérations :
![]()
![]()
![]()
Pour que la distance entre la droite et le plan soit équivalente à la distance entre le point et le plan calculée :
![]()
Évidemment, la distance doit toujours nous donner une valeur positive, car les distances sont toujours positives. Si nous obtenons un résultat négatif, cela signifie que nous avons fait une erreur en faisant une étape.