▷ Dérivée d'une soustraction (formule et exercices résolus)

Dans cet article, nous expliquons comment dériver une soustraction de fonctions (formule). Vous trouverez également des exemples de dérivées de soustractions et des exercices résolus étape par étape pour vous entraîner.

Formule pour la dérivée d’une soustraction

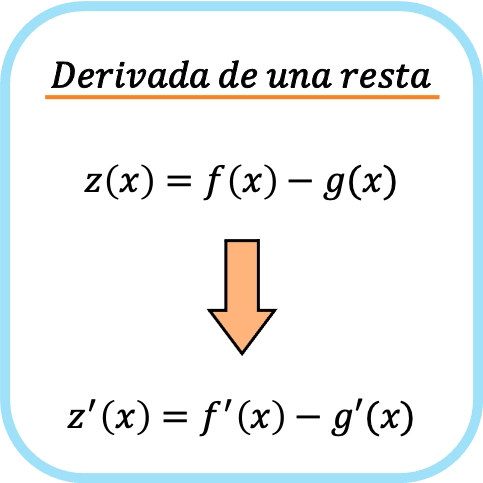
La dérivée d’une soustraction de deux fonctions est égale à la soustraction de la dérivée de chaque fonction séparément.

$z(x)=f(x)-g(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=f'(x)-g'(x)$

Autrement dit, différencier deux fonctions séparément puis les soustraire équivaut à soustraire d’abord les fonctions puis à prendre la dérivée.

De même, la même règle de dérivation s’applique aux soustractions de deux fonctions ou plus, donc si nous avons une soustraction de trois, quatre, cinq,… fonctions, nous devons différencier chacune séparément puis les soustraire.

$\begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}$

Comme vous pouvez le constater, la formule de la dérivée d’une différence de fonctions est très similaire à la règle de la dérivée d’une somme.

➤ Voir : dérivée d’une somme de fonctions

Exemples de dérivée d’une soustraction

Une fois que nous avons vu quelle est la formule de la dérivée d’une soustraction, nous passons maintenant à l’analyse de plusieurs exemples de dérivées de ce type d’opérations pour bien comprendre comment sont dérivées les soustractions de fonctions.

Exemple 1 : Dérivée d’une soustraction de fonctions potentielles

$f(x)=x^3-4x$

La dérivée de la soustraction de deux fonctions est équivalente à la différence des dérivées de chaque fonction séparément. Nous allons donc d’abord calculer la dérivée de chaque fonction séparément :

$\cfrac{d}{dx} \ x^3=3x^2$

$\cfrac{d}{dx}\ 4x=4$

La dérivée de la fonction entière est donc la suivante :

$f'(x)=3x^2-4$

Exemple 2 : Dérivée d’une soustraction de différentes fonctions

$f(x)=\text{cos}(x)-\log_7(x^2)$

Pour différencier les fonctions de soustraction, il faut d’abord différencier les deux fonctions séparément puis les soustraire.

$\cfrac{d}{dx} \ \text{cos}(x)=-\text{sen}(x)$

$\cfrac{d}{dx}\ \log_7 (x^2)=\cfrac{2x}{x^2\cdot \ln(7)}=\cfrac{2}{x\ln(7)}$

Et après avoir fait les deux dérivées, on les soustrait avec le même ordre initial :

$f'(x)=-\text{sen}(x)-\cfrac{2}{x\ln(7)}$

Exemple 3 : Dérivée d’une soustraction au carré

$f(x)=\left(x^7-2x^3-9\right)^2$

Dans ce cas, nous avons une fonction composite, car il s’agit d’une soustraction entre trois fonctions au carré. Il faut donc utiliser la formule de la dérivée d’une fonction potentielle et la règle de la chaîne pour calculer la dérivée de la fonction entière :

$f(x)=2\left(x^7-2x^3-9\right)\cdot \left(7x^6-6x^2\right)$

➤ Voir : formule de la dérivée d’une puissance

Exercices résolus sur la dérivée d’une soustraction

Dérivez les soustractions de fonctions suivantes :

$\text{A) } f(x)=9x^3-5x$

$\text{B) } f(x)=4x^5-6x^4-x^2-4$

$\text{C) } f(x)=\left(-3x^7-2x^5\right)^4$

$\text{D) } f(x)=\ln(5x^2+3x)-\text{cos}(x)$

$\text{E) } f(x)=8x^3-e^{5x}-\sqrt{8x+2}$

Voir la solution

$\text{A) } f'(x)=27x^2-5$

$\text{B) } f'(x)=20x^4-24x^3-2x$

$\text{C) } f'(x)=4\left(-3x^7-2x^5\right)^3\cdot (-21x^6-10x^4)$

$\text{D) } f'(x)=\cfrac{10x+3}{5x^2+3x}-\bilg(-\text{sen}(x)\bigr)=\cfrac{10x+3}{5x^2+3x}+\text{sen}(x)$

$\text{E) } f'(x)=24x^2-5e^{5x}-\cfrac{8}{2\sqrt{8x+2}}=24x^2-5e^{5x}-\cfrac{4}{\sqrt{8x+2}}$

Démonstration de la dérivée d’une soustraction

Ensuite, nous démontrerons la formule de la dérivée d’une soustraction de fonctions à partir de la définition de la dérivée, qui est :

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Donc si z est la différence de deux fonctions différentes :

$z(x)=f(x)-g(x)$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{z(x+h)-z(x)}{h}$

On remplace z par la soustraction des fonctions dans l’expression limite :

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)-g(x+h)\bigr]-\bigl[f(x)-g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-g(x+h)-f(x)+g(x)}{h}$

Nous allons maintenant faire une transformation pour séparer la fraction et obtenir une soustraction de deux fractions :

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}+\frac{-g(x+h)+g(x)}{h}\right]$

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}-\frac{g(x+h)-g(x)}{h}\right]$

En appliquant les lois des limites, nous pouvons séparer l’expression ci-dessus en deux limites différentes. Parce que la limite d’une soustraction est égale à la soustraction des limites :

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}-\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

Si vous regardez bien, chaque limite correspond à la dérivée d’une fonction, ce qui signifie que la formule de la dérivée d’une différence est remplie :

$\displaystyle z'(x)=f'(x)-g'(x)$