Dérivée d’un produit (ou multiplication)

Dans cet article, nous expliquons comment dériver le produit de deux fonctions (formule). De plus, vous pourrez voir plusieurs exemples de dérivées de produits de fonctions et même vous entraîner avec des exercices résolus sur les dérivées de multiplications.

Formule pour la dérivée d’un produit

La dérivée d’un produit de deux fonctions différentes est égale au produit de la dérivée de la première fonction par la deuxième fonction indifférenciée plus le produit de la première fonction indifférenciée par la dérivée de la deuxième fonction.

Autrement dit, si f(x) et g(x) sont deux fonctions différentes, la formule de la dérivée de la multiplication entre les deux fonctions est la suivante :

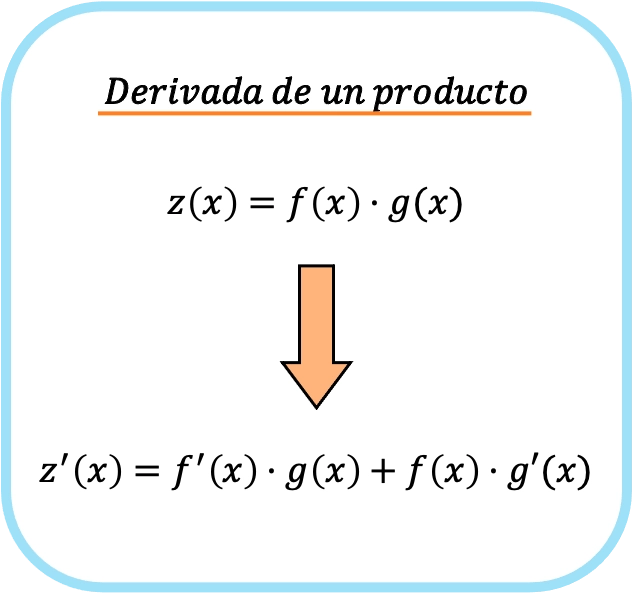
Ainsi, en appliquant la règle de la dérivée d’un produit, on passe d’une simple multiplication à deux produits différents.

Exemples de dérivé d’un produit

Une fois que nous savons quelle est la formule de la dérivée d’un produit (ou d’une multiplication), nous allons résoudre plusieurs exemples de ce type de dérivées. Cela vous permettra de comprendre beaucoup plus facilement comment est dérivé un produit de deux fonctions.

Exemple 1

Dans cet exemple nous allons résoudre la dérivée de deux fonctions potentielles en multipliant :

Comme nous l’avons vu dans la section précédente, la formule de la dérivée d’une multiplication est :

Par conséquent, nous devons d’abord calculer la dérivée de chaque fonction séparément :

Et une fois que nous connaissons la dérivée de chaque fonction, nous pouvons appliquer la formule de la dérivée du produit de deux fonctions. Autrement dit, nous multiplions la dérivée du premier facteur par le deuxième facteur sans différencier, puis ajoutons le produit du premier facteur sans différencier par la dérivée du deuxième facteur :

Enfin, nous effectuons les opérations pour simplifier le résultat obtenu :

Exemple 2

Dans ce cas nous dériverons le produit d’une constante par une fonction :

La règle de dérivée d’un produit est la suivante :

Ainsi, nous dérivons séparément chaque fonction qui fait partie du produit :

Et puis on applique la règle de la dérivée d’une multiplication :

Notez que la dérivée d’une constante est toujours nulle, on peut donc en déduire que la dérivée de la multiplication d’une constante par une fonction est égale au produit de la constante et de la dérivée de la fonction.

Exemple 3

Résolvons le produit entre une fonction exponentielle et un logarithme népérien :

La formule de la dérivée d’une multiplication de deux fonctions est :

Nous devons donc d’abord faire séparément la dérivée de chaque fonction qui forme le produit, qui sont les suivantes :

Le produit dérivé des fonctions est donc :

Exercices résolus sur la dérivée d’un produit

Dérive les produits de fonctions suivants :

Dérivé d’un produit à trois fonctions

Ensuite, nous vous laissons avec la formule de la dérivée de la multiplication de 3 fonctions, car elle est très similaire à celle de 2 fonctions et peut être utile dans certains cas.

La dérivée d’un produit de trois fonctions est égale au produit de la dérivée de la première fonction par les deux autres fonctions, plus le produit de la dérivée de la deuxième fonction par les deux autres fonctions, plus le produit de la dérivée de la troisième fonction.fonction par les deux autres fonctions.

Par exemple, si l’on veut dériver la multiplication suivante de trois fonctions différentes :

Pour résoudre la dérivée, nous devons appliquer la règle de la dérivée du produit de trois fonctions, donc :

Démonstration de la formule du dérivé d’un produit

Enfin, nous démontrerons la formule de la dérivée d’une multiplication. Vous n’êtes pas obligé de le mémoriser, mais il est toujours bon de comprendre d’où viennent les formules. 🙂

A partir de la définition mathématique de la dérivée :

Soit la fonction z le produit de deux fonctions différentes :

Alors la dérivée de z , selon la définition, sera :

Comme nous le savons, si l’on ajoute un terme en ajoutant et en soustrayant, cela n’affecte pas le résultat tant que les deux sont le même terme. Nous pouvons donc passer à l’étape suivante :

Nous utilisons maintenant les propriétés des limites pour séparer la limite précédente en deux limites différentes :

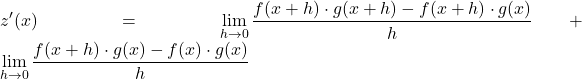
On extrait le facteur commun au numérateur des deux fractions :

En revanche, on connaît le résultat de la limite suivante :

On peut donc simplifier les limites :

Enfin, si l’on regarde les deux limites restantes, chacune correspond à la définition de la dérivée d’une fonction. L’égalité peut donc être simplifiée :

Ou équivalent: