Dérivé de l'arc cosinus

Nous expliquons ici comment dériver l’arccosinus d’une fonction. De plus, vous trouverez des exemples de dérivées de l’arc cosinus et vous pourrez vous entraîner avec des exercices résolus pas à pas. Enfin, nous vous montrons la preuve de la formule de la dérivée arccosinus.

Quelle est la dérivée de l’arc cosinus ?

La dérivée de l’arccosinus de x est moins un sur la racine carrée de un moins x au carré.

$f(x)=\text{arccos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{\sqrt{1-x^2}}$

Par conséquent, la dérivée de l’arccosinus d’une fonction est égale à moins le quotient de la dérivée de cette fonction divisé par la racine carrée de un moins cette fonction au carré.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

En fait, la première formule est obtenue en substituant u à x dans la deuxième formule. Donc, pour récapituler, la formule de la dérivée du cosinus inverse est :

Comme vous pouvez le voir, la formule de la dérivée de l’arc cosinus est comme la dérivée de l’arc sinus , mais en ajoutant un négatif avant.

Exemples de la dérivée de l’arc cosinus

Étant donné la formule de la dérivée de la fonction arccosinus, nous allons maintenant analyser plusieurs exemples de ce type de dérivées trigonométriques. De cette façon, il vous sera plus facile de comprendre comment l’arc cosinus d’une fonction est dérivé.

Exemple 1 : Dérivée de l’arc cosinus de 2x

$f(x)=\text{arccos}(2x)$

Pour résoudre la dérivée de l’arc cosinus, on utilise sa formule :

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

La dérivée de 2x est 2, donc la dérivée de l’arc cosinus de 2x est moins 2 sur la racine un moins 2x au carré :

$f(x)=\text{arccos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\sqrt{1-(2x)^2}}=-\cfrac{2}{\sqrt{1-4x^2}}$

Exemple 2 : Dérivée de l’arc cosinus de x au carré

$f(x)=\text{arccos}(x^2)$

Nous appliquons la formule de la dérivée de l’arccosinus avec la règle de la chaîne pour calculer la dérivée :

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Puisque la dérivée de la fonction x ² est 2x, la dérivée de l’arc cosinus de x à la puissance 2 est la suivante :

$f(x)=\text{arccos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=-\cfrac{2x}{\sqrt{1-x^4}}$

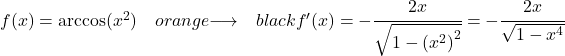
Exemple 3 : Dérivée de l’arccosinus d’un logarithme

$f(x)=\text{arccos}\bigl(\ln (x)\bigr)$

La fonction dans cet exemple est une fonction composée d’un arccosinus et d’un logarithme naturel, nous devons donc utiliser la règle de la chaîne pour la dériver.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

La dérivée du logarithme népérien est un divisé par x, par conséquent, la dérivée de la fonction entière est :

$f(x)=\text{arccos}\bigl(\ln (x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\cfrac{1}{x}}{\sqrt{1-\left(\ln(x)\right)^2}}=\cfrac{1}{x\sqrt{1-\ln^2(x)}}$

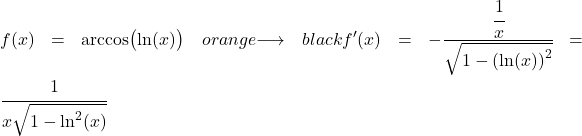
Problèmes résolus de la dérivée arccosinus

Dérivez les fonctions arccosinus suivantes :

$\text{A) }f(x)=\text{arccos}(7x)$

$\text{B) }f(x)=\text{arccos}(x^3+6x)$

$\text{C) }f(x)=\text{arccos}^3\left(e^{3x}\right)$

$\text{D) }f(x)=\text{arccos}\left(\log_3(x^3)\right)$

$\text{E) }f(x)=\text{arccos}\left(\sqrt{4x}\right)$

voir solution

$\text{A) }f'(x)=-\cfrac{7}{\sqrt{1-(7x)^2}}=-\cfrac{7}{\sqrt{1-49x^2}}$

$\text{B) }f'(x)=-\cfrac{3x^2+6}{\sqrt{1-(x^3+6x)^2}}$

$\begin{aligned}\text{C) }\displaystyle f'(x)&=3\text{arccos}^2\left(e^{3x}\right)\cdot \left(-\frac{3e^{3x}}{\sqrt{1-\left(e^{3x}\right)^2}}\right)\\[1.5ex] &=-\cfrac{9\text{arccos}^2\left(e^{3x}\right)\cdot e^{3x}}{\sqrt{1-e^{6x}}}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)&=-\cfrac{1}{\sqrt{1-\left(\log_3(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 3}\\[1.5ex] &=-\cfrac{1}{x\cdot \ln 3\cdot \sqrt{1-\log_3^2(3x)}} \end{aligned}$

$\begin{aligned}\text{E) } f'(x)& =-\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=-\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=-\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}$