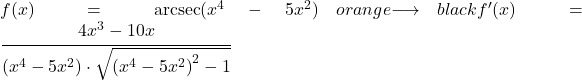Sur cette page, vous verrez quelle est la dérivée de l’arcsecant (formule). Vous trouverez des exercices résolus de dérivées de l’arcsecante d’une fonction.
Formule dérivée arcsecante
La dérivée de l’arcsecante de x est un sur le produit de x fois la racine de x au carré moins 1.
![]()
Par conséquent, la dérivée de l’arcsecante d’une fonction est égale au quotient de la dérivée de cette fonction divisé par la fonction multipliée par la racine de cette fonction au carré moins un.
![]()
De toute évidence, la deuxième formule est similaire à la première formule, la seule différence entre les deux est que la règle de la chaîne est appliquée dans la deuxième formule.

Bien que cela puisse sembler étrange car ce sont des fonctions inverses, la dérivée de l’arcsecante n’a rien à voir avec la dérivée de la sécante. Vous pouvez voir la formule de la dérivée de la sécante en cliquant ici :
➤ Voir : dérivée de sécante
Exemples de dérivée de l’arcsecante
Exemple 1
Dans cet exemple, nous verrons de combien est la dérivée de l’arcsecante de la fonction linéaire 7x.
![]()
Pour trouver la dérivée de l’arcsecante il faut appliquer sa formule correspondante, qui est la suivante :
![]()
La dérivée de la fonction 7x est 7, donc la dérivée de l’arcsecante de la fonction 7x est :
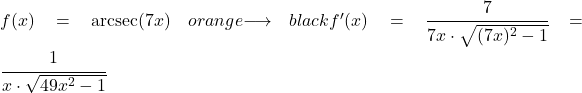
Exemple 2
Dans ce deuxième exemple, nous dériverons l’arcsecante d’une fonction potentielle.
![]()
Puisqu’il y a un terme autre que x dans l’argument de la fonction arcsecante, nous devons appliquer la règle de dérivée arcsecante avec la règle de chaîne pour dériver la fonction entière.
![]()
Ainsi, au numérateur nous écrivons la dérivée de l’argument de la fonction, et au dénominateur nous réécrivons la fonction potentielle et la multiplions par la racine carrée de la fonction de l’argument élevé à la puissance 2 moins 1 :