Décomposition (ou expression) polynomiale d’un nombre

Sur cette page, nous expliquons comment faire la décomposition (ou expression) polynomiale d’un nombre. Ici vous pouvez voir des exemples de décompositions polynomiales et, en plus, vous trouverez des exercices résolus étape par étape pour vous entraîner.

Qu’est-ce que la décomposition polynomiale d’un nombre ?

En mathématiques, la décomposition polynomiale d’un nombre consiste à exprimer ce nombre dans une somme, de sorte que chaque terme de la somme soit un produit de chaque chiffre du nombre par une puissance de base 10.

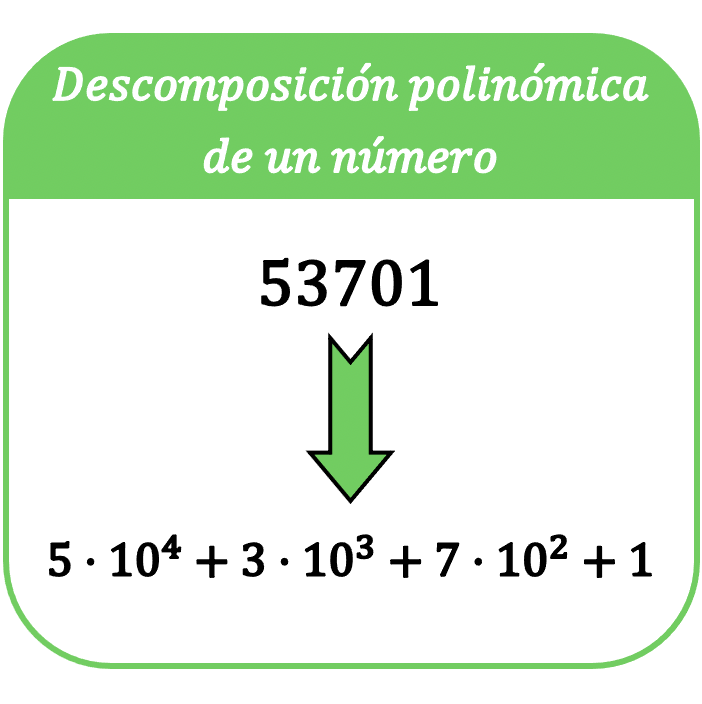
Le terme décomposition polynomiale d’un nombre est également connu sous le nom d’expression polynomiale d’un nombre .

Comment faire une décomposition polynomiale

Pour effectuer la décomposition polynomiale d’un nombre, vous devez multiplier chaque chiffre du nombre par 10 élevé au nombre de chiffres de droite .

Par exemple, si l’on veut calculer la décomposition polynomiale du nombre suivant :

Dans ce cas, le chiffre 8 occupe la cinquième position, il a donc 4 chiffres à sa droite. Il faut donc multiplier huit par dix puissance quatre :

Ainsi, pour décomposer polynomialement le nombre 86293 il faut faire de même avec tous les chiffres du nombre, et exprimer toutes les multiplications sous forme d’une somme :

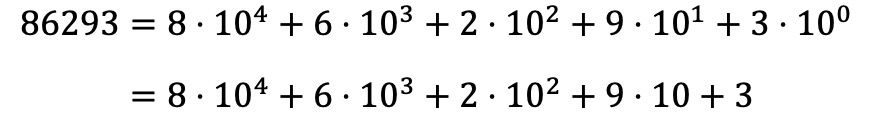
Notez que la puissance 10 ⁰ disparaît car, selon les propriétés des puissances, tout nombre élevé à 0 est égal à 1, donc 10 ⁰ =1.

D’autre part, vous pouvez également trouver la décomposition polynomiale d’un nombre à partir de sa décomposition multiplicative :

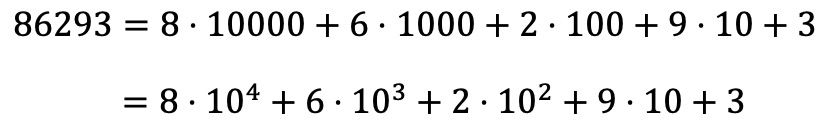
Exemples de décompositions polynomiales de nombres

Une fois que nous aurons vu comment s’effectue la décomposition polynomiale d’un nombre, nous allons voir différents exemples de ce type d’opération pour bien comprendre le concept.

• Décomposition polynomiale de 3641 :

• Décomposition polynomiale de 56912 :

• Décomposition polynomiale de 27084 :

Dans ce dernier exemple, nous pouvons simplifier la troisième multiplication puisque tout nombre multiplié par zéro s’annule.

Décomposition polynomiale de nombres décimaux

Nous venons de voir comment effectuer la décomposition polynomiale des nombres naturels. Mais… comment décomposer un nombre décimal de manière polynomiale ?

Eh bien, la décomposition polynomiale avec des nombres décimaux se fait de la même manière qu’avec des nombres entiers mais, en plus, on ajoute le produit de chaque chiffre décimal multiplié par une puissance de base 10 dont l’exposant est la position décimale occupée par ledit chiffre avec un signe négatif .

Expliqué avec des mots cela peut paraître très compliqué, mais vous verrez qu’avec un exemple cela se comprend mieux :

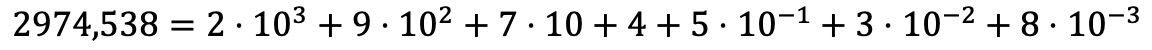
Exercices résolus de décomposition polynomiale

Pour que vous puissiez vous entraîner à faire des décompositions polynomiales, nous vous avons préparé plusieurs exercices résolus étape par étape.

N’oubliez pas que vous pouvez nous poser toutes vos questions dans les commentaires ! 🤔🤔🤔

Exercice 1

Effectuez la décomposition polynomiale des nombres suivants :

Pour trouver la décomposition polynomiale d’un nombre quelconque, multipliez chaque chiffre de ce nombre par 10 par le nombre de chiffres à droite, puis additionnez toutes les multiplications. Pourtant:

Exercice 2

Trouvez la décomposition polynomiale des nombres suivants :

Pour décomposer polynomialement un nombre, il faut multiplier chaque chiffre dudit nombre par dix par le nombre de chiffres à sa droite, puis additionner tous les produits. Pourtant:

Exercice 3

Calculez la décomposition polynomiale des nombres décimaux suivants :

Dans ce problème tous les nombres sont décimaux, donc pour les décomposer il faut multiplier chaque chiffre non décimal par 10 élevé au nombre de chiffres qu’il possède jusqu’à la virgule, et multiplier chaque chiffre décimal par 10 élevé à sa position décimale avec un signe négatif.