▷ Zusammensetzung von Funktionen (oder zusammengesetzte Funktion)

In diesem Artikel erklären wir, was die zusammengesetzte Funktion (oder Zusammensetzung von Funktionen) ist. Darüber hinaus können Sie mehrere Beispiele für zusammengesetzte Funktionen sehen und erfahren, wie der Definitionsbereich dieser Art von Funktionen berechnet wird. Schließlich finden Sie die Eigenschaften der Funktionskomposition und mehrere Schritt-für-Schritt-Übungen zum Üben.

Was ist Funktionskomposition?

Bei der Funktionszusammensetzung wird nacheinander derselbe Wert der unabhängigen Variablen (x) in zwei oder mehr Funktionen ausgewertet. Das Zusammensetzen der Funktionen (gof)(x) ergibt beispielsweise die zusammengesetzte Funktion g[f(x)].

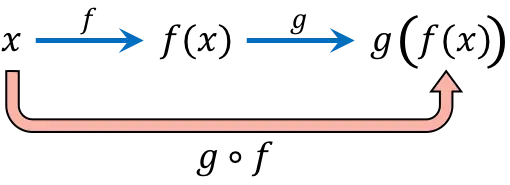
Der Ausdruck der zusammengesetzten Funktion

$g\circ f$

wir lesen „f zusammengesetzt mit g“ oder „f gefolgt von g“.

Beachten Sie, dass die Reihenfolge bei der Funktionskomposition wichtig ist. Die Funktion rechts vom Kompositionssymbol wird zuerst angewendet

$(f)$

dann die Funktion links vom Kompositionssymbol

$(g).$

Beispiel für eine Funktionskomposition

Sehen wir uns anhand der Definition einer zusammengesetzten Funktion ein Beispiel an, wie die Zusammensetzung zweier Funktionen berechnet wird.

Angesichts der folgenden zwei unterschiedlichen Funktionen:

$f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}$

Berechnen Sie die zusammengesetzte Funktion

$\left(g \circ f\right)(x)$

und bewerten Sie es in

$x=3.$

Die Zusammensetzung der Funktionen

$\left(g \circ f\right)(x)$

Das bedeutet, dass wir die folgende zusammengesetzte Funktion ausführen müssen:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Um es zu lösen, ersetzen wir

$f(x)$

durch seinen algebraischen Ausdruck:

$g\Big(f(x)\Big)= g\Big(3x+1\Big)$

Und jetzt übernehmen wir die Funktion von

$g(x)=\cfrac{x+4}{2}$

und wir setzen den Ausdruck

$3x+1$

wo es eins gibt

$x:$

$g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}$

Auf diese Weise haben wir bereits die aus g zusammengesetzte Funktion f berechnet:

$\left(g \circ f\right)(x)=\cfrac{3x+5}{2}$

Schließlich bewerten wir die zusammengesetzte Funktion in

$x=3$

Berechnen Sie einfach das Bild der Funktion in diesem Wert:

$\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7$

Zusammengesetzte Funktionsdomäne

Wenn wir Operationen an Funktionen ausführen, ist der Definitionsbereich der resultierenden Funktion normalerweise der Schnittpunkt der Definitionsbereiche der ursprünglichen Funktionen. Diese Eigenschaft wird jedoch durch die Funktionszusammensetzung nicht erfüllt.

Der Bereich der Funktionszusammensetzung

$(g\circ f)(x)$

ist äquivalent zur Menge aller Werte von x im Definitionsbereich der Funktion

$f$

wie zum Beispiel

$f(x)$

gehört zum Funktionsbereich

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

Um den Definitionsbereich einer zusammengesetzten Funktion zu berechnen, müssen Sie daher zunächst den Definitionsbereich jeder Funktion einzeln und dann den Definitionsbereich der aus der Operation resultierenden Funktion ermitteln. Somit besteht der Zusammensetzungsbereich der Funktionen aus allen Werten, die die vorherige mathematische Bedingung erfüllen.

👉 Denken Sie daran: Wenn Sie auf ein Problem stoßen, von dem Sie nicht wissen, wie Sie es lösen können, können Sie uns in den Kommentaren unten fragen!

Eigenschaften der Funktionszusammensetzung

Zusammengesetzte Funktionen haben die folgenden Eigenschaften:

Die Zusammensetzung von Funktionen hat die assoziative Eigenschaft, daher ist die folgende Gleichung immer wahr:

$f\circ (g\circ h)=(f\circ g)\circ h$

Im Allgemeinen ist die Funktionszusammensetzung nicht kommutativ, daher bestimmt die Reihenfolge der Operation das Ergebnis:

$f\circ g\neq g\circ f$

Das neutrale Element der Funktionszusammensetzung entspricht der Identitätsfunktion
$f(x)=x.$

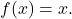
Somit ergibt jede mit der Identitätsfunktion zusammengesetzte Funktion die Funktion selbst:

$f\circ id = id \circ f = f$

$id = x$

Die Berechnung der Umkehrung der Zusammensetzung zweier Funktionen entspricht der Ermittlung der Umkehrung jeder Funktion und der anschließenden Bestimmung der zusammengesetzten Funktion:

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

Die Umkehrfunktion fungiert auch als symmetrisches Element der zusammengesetzten Funktion, da die Zusammensetzung einer Funktion mit ihrer Umkehrung der Identitätsfunktion entspricht:

$(f\circ f^{-1})^{-1}=(f^{-1}\circ f)=id=x$

Die Ableitung der Zusammensetzung zweier Funktionen wird nach der Kettenregel berechnet:

$\bigl(g\circ f\bigr)'(x)=g'\Bigl(f(x)\Bigr)\cdot f'(x)$

➤ Siehe: Was ist die Kettenregel?

Gelöste Übungen zur Zusammensetzung von Funktionen

Übung 1

Angesichts der folgenden zwei Funktionen:

$f(x)=x-2 \qquad g(x)= 5x + 4$

Berechnen Sie die Zusammensetzungen der mit g zusammengesetzten Funktionen f und mit f zusammengesetzten g .

$(g\circ f)(x)$

$(f\circ g)(x)$

Sehen Sie sich die Lösung an

Die Zusammensetzung der Funktionen

$\left(g \circ f\right)(x)$

bedeutet, die folgende zusammengesetzte Funktion zu berechnen:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Um das Problem zu lösen, ersetzen wir

$f(x)$

für seinen Ausdruck:

$f(x)=x-2$

$g\Big(f(x)\Big)= g\Big(x-2\Big)$

UND

$g\Big(x-2\Big)$

Dies bedeutet, dass im Ausdruck von

$g(x) =5x+4$

Sie müssen die Variable ersetzen

$x$

Für

$x-2:$

$g\Big(x-2\Big) = 5(x-2) +4= 5x-10+4 = 5x-6$

Noch:

$\bm{\left(g \circ f\right)(x) = 5x-6}$

Um andererseits die aus f zusammengesetzte Funktion g zu finden, müssen Sie dasselbe Verfahren durchführen, jedoch in umgekehrter Reihenfolge:

$\begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}$

Diese Übung demonstriert auch die Eigenschaft, dass zusammengesetzte Funktionen nicht kommutativ sind, da das Ergebnis von der Reihenfolge abhängt, in der die Funktionen angewendet werden.

Übung 2

Angesichts der folgenden zwei Funktionen:

$\displaystyle f(x) =x^2-3 \qquad g(x)=\frac{2x+3}{x+4}$

Berechnet die Zusammensetzung von Funktionen f, die mit g zusammengesetzt sind.

$(g\circ f)(x)$

Sehen Sie sich die Lösung an

Die aus g zusammengesetzte Funktion f bedeutet, die folgende zusammengesetzte Funktion zu lösen:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Wir ersetzen daher die Funktion f(x) durch ihren Ausdruck:

$g\Big(f(x)\Big)= g\Big(x^2-3 \Big)$

Und jetzt müssen wir ersetzen

$x$

Für

$x^2-3$

im Ausdruck der Funktion g(x):

$\begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}$

Kurz gesagt ist das Ergebnis der Funktionskomposition:

$\bm{\left(g \circ f\right)(x) =} \cfrac{\bm{2x^2-3}}{\bm{x^2+1}}$

Übung 3

Gegeben sind die folgenden zwei quadratischen Funktionen:

$\displaystyle f(x) =x^2 \qquad g(x)=g(x)= x^2-4x+8$

Bestimmen Sie das Ergebnis der folgenden Funktionszusammensetzung:

$(g\circ f)(2)$

Sehen Sie sich die Lösung an

$\left(g \circ f\right)(2)$

besteht darin, die folgende zusammengesetzte Funktion zu finden:

$\left(g \circ f\right)(2) = g\Big(f(2)\Big)$

Um die zusammengesetzte Funktion zu lösen, berechnen wir zunächst

$f(2) :$

$f(x)=x^2$

$f(2)=2^2=4$

Daher als

$f(2)=4 :$

$\left(g \circ f\right)(2) = g\Big(f(2)\Big) = g\big(4\big)$

Um den Wert der zusammengesetzten Funktion zu finden, müssen Sie also nur berechnen

$g(4) :$

$\begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}$

Zusammenfassend ist das Ergebnis des Funktionskompositionsproblems:

$\bm{\left(g \circ f\right)(2) =8}$

Übung 4

Angesichts der folgenden zwei Funktionen:

$\displaystyle f(x)=\frac{2x-2}{-x+7}\qquad g(x)= x^2-1$

Finden Sie das Ergebnis von g zusammengesetzt mit f bei x=2:

$(f\circ g)(2)$

Sehen Sie sich die Lösung an

In diesem Fall müssen wir die folgende zusammengesetzte Funktion berechnen:

$\left(f \circ g\right)(2) = f\Big(g(2)\Big)$

Also zuerst finden wir

$g(2) :$

$g(x)=x^2-1$

$g(2)=2^2-1=4-1 = 3$

Und so, so

$g(2)=3 :$

$\left(f \circ g\right)(2) = f\Big(g(2)\Big) = f\big(3\big)$

Um die zusammengesetzte Funktion zu lösen, müssen wir also berechnen

$f(3) :$

$\begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}$