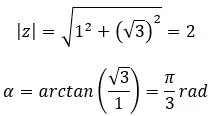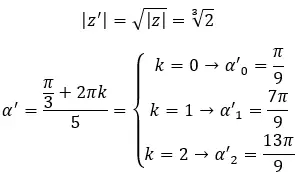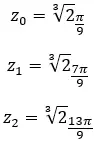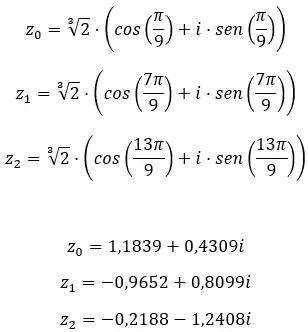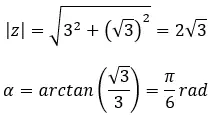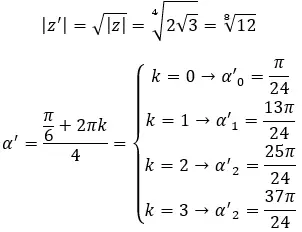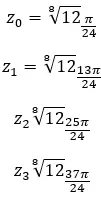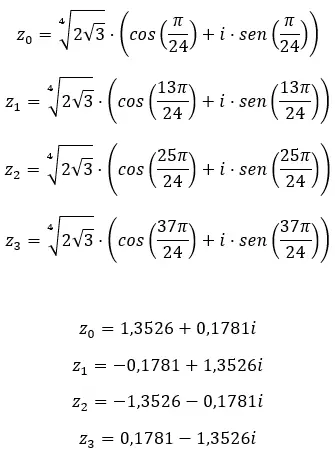Die Berechnung der Wurzeln komplexer Zahlen ist recht einfach. Nun, wenn man das Verfahren erst einmal verstanden hat, ist es ziemlich eintönig. Als nächstes erklären wir es und geben Ihnen ein Beispiel, damit Sie lernen können, wie Sie es in realen Übungen anwenden können.
n-te Wurzeln komplexer Zahlen
Das Konzept der n-ten Wurzel entspricht der Aussage „Wurzel der Ordnung n“. Daher wird die gleiche Methode zur Berechnung der Quadratwurzel und der fünften Wurzel einer komplexen Zahl verwendet. Abhängig von dieser Reihenfolge ändert sich natürlich die Anzahl der Lösungen.
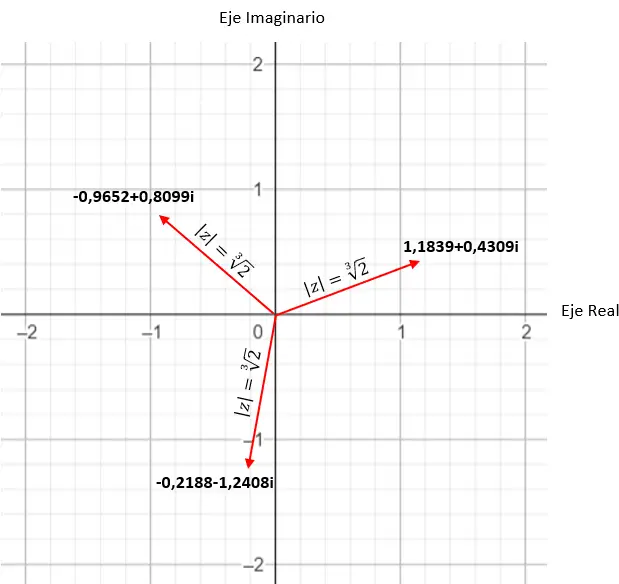
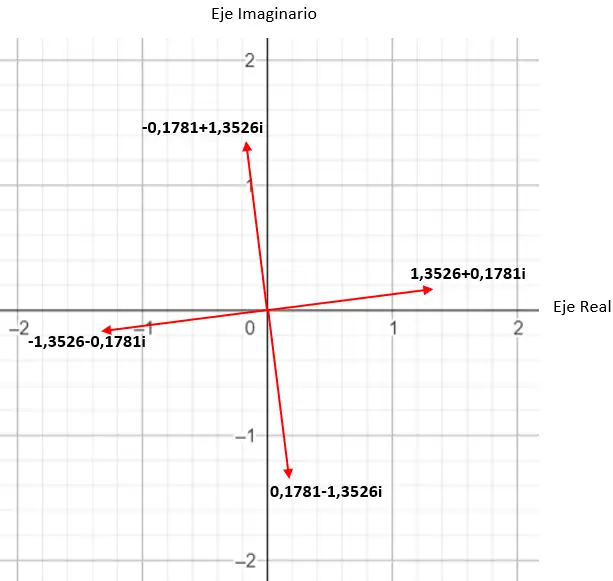
Wenn wir beispielsweise die vierte Wurzel eines Komplexes berechnen, erhalten wir 4 verschiedene Lösungen. Und wenn wir es in der komplexen Ebene ausdrücken, sehen wir, dass ein regelmäßiges Polygon mit vier Seiten entsteht, das im Ursprung der Ebene zentriert ist. Dies ist eine sehr interessante Eigenschaft, die wir später im Detail sehen werden (im Beispielabschnitt).
Nachdem wir dieses Konzept nun geklärt haben, werden wir sehen, wie man die Wurzel einer komplexen Zahl in Polarform berechnet (diese Notation ist zum Lösen einer Wurzel am bequemsten). Sie müssen lediglich die Wurzel des Moduls berechnen und das Argument durch n ausdrücken. Mit anderen Worten, die Wurzel der folgenden komplexen Zahl (z):
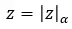
Diese Beträge berechnen:
- Modul: Die n-te Wurzel des ursprünglichen Moduls.
- Argument: Addiere 2πk im Bogenmaß oder 360k in Grad zum Argument und dividiere durch n.
Mathematisch gesehen verwenden wir zur Berechnung des Moduls und des Arguments die folgenden zwei Formeln:
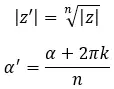
Wobei k = 0, 1, 2, …, n-1.
Und deshalb drücken wir das Ergebnis wie folgt aus:
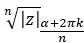
Um es klar auszudrücken: Die n Lösungen, die wir durch Lösen dieser Wurzel erhalten, werden durch denselben Modul und n verschiedene Argumente gebildet.
Beispiele für die Berechnung der n-ten Wurzeln von Komplexen
Wir werden nun einige Beispiele zur Berechnung der n-ten Wurzeln komplexer Zahlen sehen. Wir empfehlen, dass Sie versuchen, sie selbst zu beheben, und sich anschließend die Lösung ansehen. Vergessen Sie nicht, dass die Methode oben erklärt wird.
Finden Sie die dritte Wurzel der komplexen Zahl: 1 + i √3 .
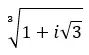
Finden Sie die vierte Wurzel der komplexen Zahl: 3+i √ 3 .
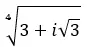
Erfahren Sie mehr über die Wurzeln komplexer Zahlen
- Komplexe Zahlen
- Operationen mit komplexen Zahlen
- komplexe Kräfte
- Eigenschaften komplexer Zahlen