Wie berechnet man die Wurzeln eines Polynoms? (gelöste Übungen)

Auf dieser Seite erfahren Sie, was die Wurzeln eines Polynoms sind und wie sie berechnet werden. Darüber hinaus können Sie Beispiele und Übungen sehen, die Schritt für Schritt zu den Wurzeln eines Polynoms gelöst werden.

Was sind die Wurzeln eines Polynoms?

In der Mathematik sind die Wurzeln (oder Nullstellen) eines Polynoms die Werte, die das Polynom aufheben. Das heißt, die Wurzeln eines Polynoms sind alle jene Werte, die bei der Auswertung im Polynom einen Zahlenwert gleich 0 haben.

Letztlich,

$x=a$

ist eine Wurzel des Polynoms

$P(x)$

$P(a)=0.$

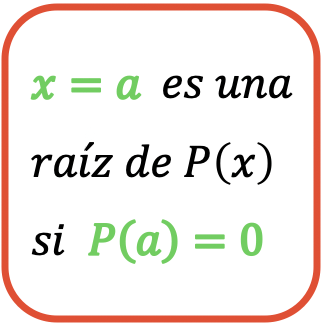
Wenn wir zum Beispiel das folgende Polynom haben:

$P(x)=x^2-3x+2$

Wir können überprüfen, dass eine der Wurzeln des Polynoms 1 ist, da der numerische Wert des Polynoms bei x=1 gleich Null ist:

$P(1)=1^2-3\cdot 1+2 = 1-3+2 \color{blue} \bm{= 0}$

Andererseits ist 3 keine Wurzel des Polynoms, da es sich nicht um einen Wert handelt, der das Polynom aufhebt, oder mit anderen Worten, der numerische Wert des Polynoms bei x=3 ist von Null verschieden:

$P(3)=3^2-3\cdot 3+2 = 9-9+2=2 \color{blue} \bm{\neq 0}$

Sie verstehen jetzt wahrscheinlich besser, was die Wurzel eines Polynoms ist, möchten aber nicht wissen, wie viele Wurzeln ein Polynom hat? Oder wie findet man alle Wurzeln eines Polynoms? Nun, genau das werden wir im nächsten Abschnitt sehen.

Wie berechnet man alle Wurzeln eines Polynoms?

Um alle Wurzeln eines Polynoms zu finden, müssen Sie die folgenden Schritte ausführen:

Zunächst werden alle Teiler des unabhängigen Termes des Polynoms berechnet.
Zweitens werden alle im vorherigen Schritt gefundenen Werte im Polynom ausgewertet.
Wenn schließlich bei der Auswertung einer Zahl im Polynom ihr numerischer Wert gleich Null ist, ist diese Zahl eine Wurzel des Polynoms. Andernfalls entspricht diese Zahl keiner Wurzel des Polynoms.

Dieses Verfahren wird aus dem Restsatz abgeleitet. Klicken Sie auf diesen Link, um den Grund für dieses spezielle Verfahren herauszufinden.

Beispiel für die Berechnung der Wurzeln eines Polynoms

Im Folgenden lösen wir Schritt für Schritt ein Beispiel, damit Sie besser verstehen, wie Sie die Wurzeln eines Polynoms ziehen.

Was sind alle Wurzeln des folgenden Polynoms?

$P(x) = x^2-5x+6$

Zunächst müssen wir die Teiler des unabhängigen Termes finden, denn jede Wurzel eines Polynoms ist auch ein Teiler des unabhängigen Termes. Die Teiler von 6 sind also:

Teiler von 6: +1, -1, +2, -2, +3, -3

Denken Sie daran: Wenn eine Zahl ein Teiler ist, ist auch ihr Negativ ein Teiler. Da eine Zahl durch positive und negative Zahlen teilbar ist.

Somit sind die möglichen Nullstellen oder Nullstellen des Polynoms: ±1, ±2, ±3. Daher müssen wir für alle diese Werte den numerischen Wert des Polynoms bestimmen. Und dazu ersetzen wir diese Werte in den Ausdruck des Polynoms, in dem es ein x gibt:

$P(1) = 1^2 -5\cdot 1 +6= 1 -5 +6 =2$

$P(-1) = (-1)^2 -5\cdot (-1) +6 =1+5+6 = 12$

$P(2) = 2^2 -5\cdot 2 +6 =4-10+6= \color{blue} \bm{0}$

$P(-2) = (-2)^2 -5\cdot (-2) +6 =4+10+6 =20$

$P(3) = 3^2 -5\cdot 3 +6 =9-15+6=\color{blue} \bm{0}$

$P(-3) = (-3)^2 -5\cdot (-3) +6 =9+15+6 =30$

Das Polynom verschwindet also nur, wenn die Variable x +2 oder +3 ist. Hier sind also die Wurzeln des Polynoms:

Nullstellen oder Nullstellen des Polynoms : +2 und +3

Beachten Sie andererseits, dass das Polynom so viele Wurzeln hat wie sein Grad, das heißt, da das Polynom zweiten Grades ist, hat es zwei Wurzeln. In den Eigenschaften der Wurzeln eines Polynoms (unten) werden wir sehen, warum diese Eigenschaft immer für jedes Polynom gilt.

Wir haben gerade eine Möglichkeit gesehen, die Wurzeln eines Polynoms zu finden. Allerdings gibt es noch andere Methoden, um dies zu erreichen, beispielsweise kann man die Wurzeln eines Polynoms auch mit der Ruffini-Regel finden. Klicken Sie auf den folgenden Link, um Beispiele der Ruffini-Regel zu sehen. Hier erfahren Sie, woraus diese bekannte Methode besteht und welche Unterschiede zwischen den beiden Verfahren bestehen.

Eigenschaften der Wurzeln eines Polynoms

Die Nullstellen oder Nullstellen eines Polynoms haben die folgenden Eigenschaften:

Wie wir zuvor gesehen haben, sind die ganzzahligen Wurzeln (oder Nullstellen) eines Polynoms Teiler des unabhängigen Termes des Polynoms.

Wenn wir alle Wurzeln eines Polynoms kennen, können wir dieses Polynom in Form von Produkten von Binomialen dieses Typs ausdrücken
$(x-a).$

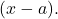
Zum Beispiel das Polynom

$P(x) =x^3+3x^2-x-3$

Es hat 3 Wurzeln, die sind

$x=+1, x=-1$

Und

$x=-3.$

Wir können das Polynom daher in Form von drei Multiplikationen von Faktoren umschreiben, die jeweils durch die Variable gebildet werden

$x$

und eine Wurzel hat das Vorzeichen geändert:

$\displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}$

$\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60}P(x) =x^3+3x^2-x-3 = (x\color{verd}\bm{-1}\color{black})\cdot (x\color{vermell}\bm{+1}\color{black}) \cdot (x\color{blau}\bm{+3}\color{black})$

Dies wird als Polynomfaktorisierung bezeichnet. Tatsächlich besteht eine der Hauptanwendungen bei der Bestimmung der Wurzeln eines Polynoms darin, dass sie zur Faktorisierung des Polynoms verwendet werden. Im folgenden Link erfahren Sie, woraus diese ganz besondere Operation besteht und können darüber hinaus mit gelösten Polynomfaktorisierungsübungen üben.

Ein Polynom hat so viele Wurzeln, wie sein Grad angibt. Ein Polynom zweiten Grades hat also zwei Wurzeln, ein Polynom dritten Grades hat drei Wurzeln, ein Polynom vierten Grades hat vier Wurzeln und so weiter.

Wenn ein Polynom keinen unabhängigen Term hat, bedeutet das, dass eine seiner Wurzeln 0 ist. Dann müssen die restlichen Wurzeln Teiler des Koeffizienten des Monoms niedrigsten Grades sein.

Das folgende Polynom hat beispielsweise keinen unabhängigen Term:

$P(x) =x^3+x^2-2x$

Daher muss eine Wurzel des Polynoms notwendigerweise 0 sein. Und die restlichen Wurzeln sind Teiler des Koeffizienten des Termes niedrigsten Grades, also -2. Genauer gesagt sind es die anderen Wurzeln

$x=+1$

Und

$x=-2,$

also sind alle Wurzeln des Polynoms:

Nullstellen oder Nullstellen des Polynoms: 0, +1 und -2

Wenn die Wurzeln eines Polynoms nicht bestimmt werden können, spricht man von einem irreduziblen Polynom.

Wir werden beispielsweise versuchen, die Wurzeln des folgenden Polynoms zu berechnen:

$P(x) =x^2+3x-1$

Die einzig möglichen Wurzeln des Polynoms sind die Teiler von -1, also -1 und +1. Daher werten wir das Polynom zu diesen Werten aus:

$P(1) = 1^2 +3\cdot 1 -1= 1 +3 -1 =3 \neq 0$

$P(-1) = (-1)^2 +3\cdot (-1)-1 =1-3-1 =-3 \neq 0$

In keinem Fall wird das Polynom aufgehoben, es hat also keine Wurzeln und ist daher ein irreduzibles Polynom.

Wenn das Polynom aus dem Produkt mehrerer Polynome besteht, ist es nicht erforderlich, dieses Produkt zur Berechnung der Wurzeln zu verwenden, sondern die Wurzeln des Polynoms sind die Wurzeln jedes multiplizierten Faktors.

Wenn wir zum Beispiel das folgende Polynom haben:

$P(x) = (x-2) \cdot (x+1)$

Aus der zweiten Eigenschaft der Wurzeln von Polynomen können wir ableiten, dass die Wurzel des linken Polynoms +2 und die Wurzel des rechten Polynoms -1 ist.

$\displaystyle (x-2) \ \longrightarrow \ \text{ra\'iz} \ x=+2$

$\displaystyle (x+1) \ \longrightarrow \ \text{ra\'iz} \ x=-1$

Somit sind die Wurzeln des Polynoms, das sich aus der Multiplikation der beiden Faktoren ergibt, ihre jeweiligen Wurzeln, also +2 und -1.

$\displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}$

Gelöste Übungen zu den Wurzeln von Polynomen

Übung 1

Bestimmen Sie, ob

$x = -4$

ist eine Wurzel des folgenden Polynoms:

$P(x)=x^3+2x^2-11x-12$

Sehen Sie sich die Lösung an

Um herauszufinden, ob

$x=-4$

eine Wurzel des Polynoms ist, müssen wir es auf diesen Wert auswerten. Noch:

$\begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}$

Der numerische Wert des Polynoms in

$x=-4$

ist Null, also ist es effektiv eine Wurzel des Polynoms.

Übung 2

Berechnen Sie alle Wurzeln des folgenden Polynoms:

$P(x)=x^2-3x+2$

Sehen Sie sich die Lösung an

Um die möglichen Wurzeln des Polynoms zu finden, müssen wir zunächst die Teiler des unabhängigen Termes finden. Die Teiler von 2 sind also:

Teiler von 2: +1, -1, +2, -2

Die möglichen Nullstellen bzw. Nullstellen des Polynoms sind daher ±1 und ±2. Daher müssen wir berechnen, wie groß das Polynom in all diesen Werten ist:

$P(1)=1^2-3\cdot 1+2 =1-3+2=0$

$P(-1)=(-1)^2-3\cdot (-1)+2 =1+3+2=6$

$P(2)=2^2-3\cdot 2+2 =4-6+2=0$

$P(-2)=(-2)^2-3\cdot (-2)+2 =4+6+2=12$

Das Polynom verschwindet also, wenn x +1 oder +2 ist. Hier sind also die Wurzeln des Polynoms:

Nullstellen oder Nullstellen des Polynoms : +1 und +2

Übung 3

Finden Sie die Wurzeln des folgenden Polynoms:

$P(x)=x^3-x^2-4x+4$

Sehen Sie sich die Lösung an

Wir müssen zunächst die Teiler des unabhängigen Termes finden, da die Wurzel eines Polynoms auch ein Teiler des unabhängigen Termes ist. Die Teiler von 4 sind also:

Teiler von 4: +1, -1, +2, -2, +4, -4

Die möglichen Nullstellen bzw. Nullstellen des Polynoms sind daher ±1, ±2 und ±4. Wir müssen daher in all diesen Werten den numerischen Wert des Polynoms finden:

$P(1)=1^3-1^2-4\cdot 1+4 =1-1-4+4=0$

$P(-1)=(-1)^3-(-1)^2-4\cdot (-1)+4 =-1-1+4+4=6$

$P(2)=2^3-2^2-4\cdot 2+4 =8-4-8+4=0$

$P(-2)=(-2)^3-(-2)^2-4\cdot (-2)+4 =-8-4+8+4=0$

$P(3)=3^3-3^2-4\cdot 3+4 =27-9-12+4=10$

$P(-3)=(-3)^3-(-3)^2-4\cdot (-3)+4 =-27-9+12+4=20$

Daher verschwindet das Polynom nur, wenn x +1, +2 oder -2 ist. Hier sind also die Wurzeln des Polynoms:

Nullstellen oder Nullstellen des Polynoms : +1, +2 und -2

Übung 4

Finden Sie die Wurzeln des folgenden Polynoms:

$P(x)=x^3-6x^2+8x$

Sehen Sie sich die Lösung an

In diesem Fall hat das Polynom keinen unabhängigen Term. Daher wissen wir gemäß der oben erläuterten vierten Eigenschaft der Wurzeln, dass eine der Wurzeln des Polynoms 0 sein muss.

Wurzeln des Polynoms:

$x=0$

Darüber hinaus sind in diesem Fall die möglichen Wurzeln nicht die Teiler des unabhängigen Termes, sondern die des Koeffizienten des Termes niedrigsten Grades, also 8:

Teiler von 8: +1, -1, +2, -2, +4, -4, +8, -8

Die möglichen Nullstellen oder Nullstellen des Polynoms sind also ±1, ±2, ±4 und ±8. Wir müssen daher den Zahlenwert des Polynoms bei all diesen Werten berechnen:

$P(1)=1^3-6\cdot 1^2+8\cdot 1 = 1-6+8=3$

$P(-1)=(-1)^3-6\cdot (-1)^2+8\cdot (-1) = -1-6-8=-15$

$P(2)=2^3-6\cdot 2^2+8\cdot 2 = 8-24+16=0$

$P(-2)=(-2)^3-6\cdot (-2)^2+8\cdot (-2) = -8-24-16=-48$

$P(4)=4^3-6\cdot 4^2+8\cdot 4 = 64-96+32=0$

$P(-4)=(-4)^3-6\cdot (-4)^2+8\cdot (-4) = -64-96-32=-192$

$P(8)=8^3-6\cdot 8^2+8\cdot 8 = 512-384+64=192$

$P(-8)=(-8)^3-6\cdot (-8)^2+8\cdot (-8) = -512-384-64=-960$

Das Polynom verschwindet also, wenn x +2 oder +4 ist, diese Werte sind also die Wurzeln des Polynoms. Allerdings müssen wir auch die Wurzel 0 hinzufügen, die wir zu Beginn des Problems gefunden haben. Zusammenfassend sind alle Wurzeln des Polynoms:

Nullstellen oder Nullstellen des Polynoms : 0, +2 und +4

Übung 5

Verwenden Sie die Eigenschaften von Wurzeln von Polynomen, um die Wurzeln des folgenden Polynoms zu berechnen:

$P(x)=(x-1)(x+3)(x^2-x-2)$

Sehen Sie sich die Lösung an

Wie wir bei der sechsten Eigenschaft der Wurzeln gesehen haben, ist es nicht notwendig, alle Wurzeln zu berechnen, wenn das Polynom durch das Produkt von Faktoren gebildet wird, da die Wurzeln des gesamten Polynoms die Wurzeln jedes Faktors sind.

Darüber hinaus können wir aus der zweiten Eigenschaft der Wurzeln von Polynomen ableiten, dass die Wurzel des ersten Faktors +1 und die Wurzel des zweiten Faktors -3 ist.

$\displaystyle (x-1) \ \longrightarrow \ \text{ra\'iz} \ x=+1$

$\displaystyle (x+3) \ \longrightarrow \ \text{ra\'iz} \ x=-3$

Wir müssen also nur die Wurzeln des letzten Faktors finden. Dazu ermitteln wir die Teiler des unabhängigen Termes (-2):

Teiler von -2: +1, -1, +2, -2

Die möglichen Nullstellen oder Nullstellen des letzten Polynoms sind also ±1 und ±2. Womit wir den numerischen Wert dieses Polynoms in all diesen Werten berechnen müssen:

$q(x)= x^2-x-2$

$q(1)=1^2-1-2=1-1-2=-2$

$q(-1)=(-1)^2-(-1)-2=1+1-2=0$

$q(2)=2^2-2-2=4-2-2=0$

$q(-2)=(-2)^2-(-2)-2=4+2-2=4$

Die Wurzeln des Polynoms auf der rechten Seite sind daher -1 und 2.

Daher sind die Wurzeln des gesamten Polynoms alle gefundenen Wurzeln:

Nullstellen oder Nullstellen des Polynoms : +1, -1, +2, -3

Wurzeln eines polynoms

Was sind die Wurzeln eines Polynoms?

Wie berechnet man alle Wurzeln eines Polynoms?

Beispiel für die Berechnung der Wurzeln eines Polynoms

Eigenschaften der Wurzeln eines Polynoms

Gelöste Übungen zu den Wurzeln von Polynomen

Übung 1

Übung 2

Übung 3

Übung 4

Übung 5

Kommentar verfassen Kommentieren abbrechen