So diagonalisieren Sie eine Matrix -

Auf dieser Seite finden Sie alles über diagonalisierbare Matrizen: Was sie sind, wann sie diagonalisiert werden können und wann nicht, die Methode zur Diagonalisierung von Matrizen, die Anwendungen und Eigenschaften dieser speziellen Matrizen usw. Und Sie haben sogar mehrere Übungen Schritt für Schritt gelöst, damit Sie üben und perfekt verstehen können, wie sie diagonalisiert werden. Schließlich lernen wir auch, wie man Matrixdiagonalisierungen mit dem Computerprogramm MATLAB durchführt, da dieses sehr häufig verwendet wird.

Was ist eine diagonalisierbare Matrix?

Wie wir weiter unten sehen werden, ist die Diagonalisierung einer Matrix im Bereich der linearen Algebra sehr nützlich. Aus diesem Grund fragen sich viele: Was ist Matrixdiagonalisierung? Nun, die Definition einer diagonalisierbaren Matrix lautet:

Eine diagonalisierbare Matrix ist eine quadratische Matrix, die in eine Diagonalmatrix umgewandelt werden kann, also eine Matrix, die außer auf der Hauptdiagonale mit Nullen gefüllt ist. Die Diagonalisierung von Matrizen gliedert sich wie folgt:

$A = PDP^{-1}$

Oder gleichwertig,

$D = P^{-1}AP$

Gold

$A$

ist die zu diagonalisierende Matrix,

$P$

ist die Matrix, deren Spalten die Eigenvektoren (oder Eigenvektoren) von sind

$A$

$P^{-1}$

seine inverse Matrix und

$D$

ist die Diagonalmatrix, die durch die Eigenwerte (oder Eigenwerte) von gebildet wird

$A$

Die Matrix

$P$

fungiert als eine Basis, die die Matrix ändert, also ändern wir mit dieser Formel tatsächlich die Basis in eine Matrix

$A$

, so dass die Matrix eine Diagonalmatrix wird (

$D$

) in der neuen Basis.

Daher die Matrix

$A$

und die Matrix

$D$

Es handelt sich um ähnliche Matrizen. Und offensichtlich,

$P$

Es handelt sich um eine reguläre oder nicht entartete Matrix.

Wann kann man eine Matrix diagonalisieren?

Nicht alle Matrizen können diagonalisiert werden; Nur Matrizen, die bestimmte Eigenschaften erfüllen, können diagonalisiert werden. Ob eine Matrix diagonalisierbar ist, lässt sich auf unterschiedliche Weise erkennen:

Eine quadratische Matrix der Ordnung n ist diagonalisierbar, wenn sie n linear unabhängige Eigenvektoren (oder Eigenvektoren) hat, oder mit anderen Worten, wenn diese Vektoren eine Basis bilden. Das liegt an der Matrix
$P$

, das zur Diagonalisierung einer Matrix verwendet wird, wird durch die Eigenvektoren dieser Matrix gebildet. Um zu wissen, ob die Eigenvektoren LI sind, reicht es aus, die Determinante der Matrix anzugeben

$P$

von 0 verschieden ist, was bedeutet, dass die Matrix den maximalen Rang hat.

$\text{si} \quad \text{det}(P)\neq 0 \ \longrightarrow \ \text{matriz diagonalizable}$

Eine Eigenschaft von Eigenwerten und Eigenvektoren besteht darin, dass Eigenvektoren verschiedener Eigenwerte linear unabhängig sind. Wenn also alle Eigenwerte der Matrix eindeutig sind, ist die Matrix diagonalisierbar.

Eine andere Möglichkeit zu bestimmen, ob eine Matrix in einer Diagonalmatrix untergebracht werden kann, ist die Verwendung algebraischer und geometrischer Multiplizitäten. Die algebraische Multiplizität ist die Häufigkeit, mit der ein Eigenwert (oder Eigenwert) wiederholt wird, und die geometrische Multiplizität ist die Dimension des Kernels (oder Kernels) der Matrix durch Subtraktion des Eigenwerts auf seiner Hauptdiagonale. Wenn also für jeden Eigenwert die algebraische Multiplizität gleich der geometrischen Multiplizität ist , ist die Matrix diagonalisierbar.

$\alpha_\lambda = \text{multiplicidad algebraica} = \text{multiplicidad del valor propio}$

$m_\lambda = \text{multiplicidad geom\'etrica} = \text{dim } Ker(A-\lambda I) = n -rg(A-\lambda I)$

$\alpha_\lambda \geq m_\lambda \geq 1$

$\text{si} \quad \alpha_\lambda = m_\lambda \quad \forall \lambda \ \longrightarrow \ \text{matriz diagonalizable}$

Schließlich gibt es noch einen Satz, den Spektralsatz, der die Diagonalisierung symmetrischer Matrizen mit reellen Zahlen garantiert. Mit anderen Worten: Jede reelle und symmetrische Matrix ist diagonalisierbar .

So diagonalisieren Sie eine Matrix

Das Verfahren zur Diagonalisierung einer Matrix basiert auf der Ermittlung der Eigenwerte (oder Eigenwerte) und Eigenvektoren (oder Eigenvektoren) einer Matrix. Aus diesem Grund ist es wichtig, dass Sie die Berechnung der Eigenwerte (oder Eigenwerte) und Eigenvektoren (oder Eigenvektoren) jeder Matrix beherrschen. Sie können sich daran erinnern, wie es gemacht wurde, indem Sie auf den Link klicken. Dort erklären wir Ihnen Schritt für Schritt, wie Sie sie finden und einige Tricks, die die Berechnungen erheblich erleichtern. Darüber hinaus finden Sie auch gelöste Übungsaufgaben zum Üben.

Mit der folgenden Methode können Sie eine Matrix beliebiger Dimension diagonalisieren: 2×2, 3×3, 4×4 usw. Die Schritte zur Diagonalisierung einer Matrix sind:

Erhalten Sie die Eigenwerte (oder Eigenwerte) der Matrix.
Berechnen Sie den Eigenvektor, der jedem Eigenwert zugeordnet ist.
Konstruieren Sie die Matrix
$P$

, deren Spalten die Eigenvektoren der zu diagonalisierenden Matrix sind.
Überprüfen Sie, ob die Matrix diagonalisiert werden kann (sie muss eine der im vorherigen Abschnitt erläuterten Bedingungen erfüllen).
Konstruieren Sie die Diagonalmatrix
$D$

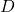
, deren Elemente alle 0 sind, mit Ausnahme derjenigen auf der Hauptdiagonale, bei denen es sich um die in Schritt 1 gefundenen Eigenwerte handelt.

Achtung: Die Eigenvektoren der Matrix

$P$

können in beliebiger Reihenfolge platziert werden, jedoch die Eigenwerte der Diagonalmatrix

$D$

Sie müssen in der gleichen Reihenfolge platziert werden. Zum Beispiel der erste Eigenwert der Diagonalmatrix

$D$

muss derjenige sein, der dem Eigenvektor der ersten Spalte der Matrix entspricht

$P$

Nachfolgend finden Sie einige Schritt-für-Schritt-Übungen zur Matrixdiagonalisierung, mit denen Sie üben können.

Übungen zur Matrixdiagonalisierung gelöst

Übung 1

Diagonalisieren Sie die folgende quadratische Matrix der Dimension 2×2:

$\displaystyle A= \begin{pmatrix}2&2\\[1.1ex] 1&3\end{pmatrix}$

Sehen Sie sich die Lösung an

Wir müssen zunächst die Eigenwerte der Matrix A bestimmen. Wir berechnen daher die charakteristische Gleichung, indem wir die folgende Determinante lösen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2- \lambda &2\\[1.1ex] 1&3-\lambda \end{vmatrix} = \lambda^2-5\lambda +4$

Berechnen wir nun die Wurzeln des charakteristischen Polynoms:

$\displaystyle \lambda^2-5\lambda +4=0 \ \longrightarrow \ \begin{cases} \lambda = 4 \\[2ex] \lambda = 1 \end{cases}$

Sobald die Eigenwerte erhalten sind, berechnen wir den jeweiligen Eigenvektor. Zunächst der Eigenvektor, der dem Eigenwert 1 entspricht:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&2\\[1.1ex] 1&2\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] x+2y = 0\end{array}\right\} \longrightarrow \ x=-2y$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] 1 \end{pmatrix}$

Und dann berechnen wir den Eigenvektor, der zum Eigenwert 4 gehört:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&2\\[1.1ex] 1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2y = 0 \\[2ex] x-y = 0\end{array}\right\} \longrightarrow \ y=x$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 1 \end{pmatrix}$

Wir bauen die Matrix

$P$

, gebildet durch die Eigenvektoren der Matrix:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix}$

Da alle Eigenwerte unterschiedlich sind, ist die Matrix A diagonalisierbar. Somit ist die entsprechende Diagonalmatrix diejenige, deren Eigenwerte auf der Hauptdiagonale liegen:

$\displaystyle D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Denken Sie daran, dass die Eigenwerte in derselben Reihenfolge platziert werden müssen, in der die Eigenvektoren in der Matrix platziert werden

$P$

Zusammenfassend sind die Basisänderungsmatrix und die diagonalisierte Matrix:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Übung 2

Diagonalisieren Sie die folgende quadratische Matrix der Ordnung 2:

$\displaystyle A= \begin{pmatrix}3&4\\[1.1ex] -1&-2\end{pmatrix}$

Sehen Sie sich die Lösung an

Wir müssen zunächst die Eigenwerte der Matrix A bestimmen. Wir berechnen daher die charakteristische Gleichung, indem wir die folgende Determinante lösen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3- \lambda &4\\[1.1ex] -1&-2-\lambda \end{vmatrix} = \lambda^2-\lambda -2$

Berechnen wir nun die Wurzeln des charakteristischen Polynoms:

$\displaystyle \lambda^2-\lambda -2=0 \ \longrightarrow \ \begin{cases} \lambda = -1 \\[2ex] \lambda = 2 \end{cases}$

Sobald die Eigenwerte erhalten sind, berechnen wir den jeweiligen Eigenvektor. Zuerst der Eigenvektor, der dem Eigenwert -1 entspricht:

$\displaystyle (A+I)v=0$

$\displaystyle \begin{pmatrix}4&4\\[1.1ex] -1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 4x+4y = 0 \\[2ex] -x-y = 0\end{array}\right\} \longrightarrow \ x=-y$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 1 \end{pmatrix}$

Und dann berechnen wir den Eigenvektor, der zum Eigenwert 2 gehört:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}1&4\\[1.1ex] -1&-4\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+4y = 0 \\[2ex] -x-4y = 0\end{array}\right\} \longrightarrow \ x=-4y$

$\displaystyle v = \begin{pmatrix}-4 \\[1.1ex] 1 \end{pmatrix}$

Wir bauen die Matrix

$P$

, gebildet durch die Eigenvektoren der Matrix:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1 \end{pmatrix}$

Da alle Eigenwerte voneinander verschieden sind, ist Matrix A diagonalisierbar. Somit ist die entsprechende Diagonalmatrix diejenige, die die Eigenwerte auf der Hauptdiagonale enthält:

$\displaystyle D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Denken Sie daran, dass die Eigenwerte in derselben Reihenfolge platziert werden müssen, in der die Eigenvektoren in der Matrix platziert werden

$P$

Zusammenfassend sind die Basisänderungsmatrix und die diagonalisierte Matrix:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1\end{pmatrix} \qquad D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Übung 3

Diagonalisieren Sie die folgende quadratische Matrix der Dimension 3×3:

$\displaystyle A= \begin{pmatrix}2&0&2\\[1.1ex] -1&2&1\\[1.1ex] 0&1&4\end{pmatrix}$

Sehen Sie sich die Lösung an

Der erste Schritt besteht darin, die Eigenwerte der Matrix A zu finden. Wir berechnen daher die charakteristische Gleichung, indem wir die Determinante der folgenden Matrix lösen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&0&2\\[1.1ex] -1&2-\lambda&1\\[1.1ex] 0&1&4-\lambda \end{vmatrix} = -\lambda^3+8\lambda^2-19\lambda+12$

Wir müssen nun die Wurzeln des charakteristischen Polynoms berechnen. Da es sich um ein Polynom dritten Grades handelt, wenden wir die Regel von Ruffini an:

$\displaystyle \begin{array}{r|rrrr} & -1&8&-19& 12 \\[2ex] 1 & & -1&7&-12 \\ \hline &-1\vphantom{\Bigl)}&7&-12&0 \end{array}$

Und dann finden wir die Wurzeln des erhaltenen Polynoms:

$\displaystyle -\lambda^2+7\lambda -12=0 \ \longrightarrow \ \begin{cases} \lambda = 3 \\[2ex] \lambda = 4 \end{cases}$

Die Eigenwerte der Matrix sind also:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 4$

Sobald die Eigenwerte gefunden wurden, berechnen wir den zu jedem von ihnen zugehörigen Eigenvektor. Zunächst der Eigenvektor, der dem Eigenwert 1 entspricht:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&0&2\\[1.1ex] -1&1&1\\[1.1ex] 0&1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2z = 0 \\[2ex] -x+y+z = 0\\[2ex] y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=-2z \\[2ex] y = -3z \end{array}$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] -3 \\[1.1ex] 1\end{pmatrix}$

Dann berechnen wir den Eigenvektor zum Eigenwert 3:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}-1&0&2\\[1.1ex] -1&-1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -x+2z = 0 \\[2ex] -x-y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=2z \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}2 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

Und schließlich berechnen wir den Eigenvektor zum Eigenwert 4:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&0&2\\[1.1ex] -1&-2&1\\[1.1ex] 0&1&0\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2z = 0 \\[2ex] -x-2y+z = 0\\[2ex] y = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=z \\[2ex] y = 0 \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 1\end{pmatrix}$

Wir bauen die Matrix

$P$

, gebildet durch die Eigenvektoren der Matrix:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1 \end{pmatrix}$

Da alle Eigenwerte voneinander verschieden sind, ist Matrix A diagonalisierbar. Somit ist die entsprechende Diagonalmatrix diejenige, deren Eigenwerte auf der Hauptdiagonale liegen:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Denken Sie daran, dass die Eigenwerte in derselben Reihenfolge platziert werden müssen, in der die Eigenvektoren in der Matrix platziert werden

$P$

Kurz gesagt sind die Basisänderungsmatrix und die diagonalisierte Matrix:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1\end{pmatrix} \qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Übung 4

Diagonalisieren Sie, wenn möglich, die folgende quadratische Matrix der Ordnung 3:

$\displaystyle A= \begin{pmatrix}-1&3&1\\[1.1ex] 0&2&0\\[1.1ex] 3&-1&1\end{pmatrix}$

Sehen Sie sich die Lösung an

Der erste Schritt besteht darin, die Eigenwerte der Matrix A zu finden. Wir berechnen daher die charakteristische Gleichung, indem wir die Determinante der folgenden Matrix lösen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}-1-\lambda&3&1\\[1.1ex] 0&2-\lambda&0\\[1.1ex] 3&-1&1-\lambda \end{vmatrix} = -\lambda^3+2\lambda^2+4\lambda-8$

Wir müssen nun die Wurzeln des minimalen Polynoms berechnen. Da es sich um ein Polynom dritten Grades handelt, wenden wir zur Faktorisierung die Regel von Ruffini an:

$\displaystyle \begin{array}{r|rrrr} & -1&2&\phantom{-}4& -8 \\[2ex] 2 & & -2&0&8 \\ \hline &-1\vphantom{\Bigl)}&0&4&0 \end{array}$

Und dann finden wir die Wurzeln des erhaltenen Polynoms:

$\displaystyle -\lambda^2+4=0 \ \longrightarrow \ \begin{cases} \lambda = +2 \\[2ex] \lambda = -2 \end{cases}$

Die Eigenwerte der Matrix sind also:

$\lambda=2 \qquad \lambda =2 \qquad \lambda = -2$

Der Eigenwert von -2 ist von einfacher algebraischer Multiplizität, der Eigenwert von 2 hingegen von doppelter Multiplizität.

Sobald die Eigenwerte gefunden wurden, berechnen wir den zu jedem von ihnen zugehörigen Eigenvektor. Zuerst der Eigenvektor, der dem Eigenwert -2 entspricht:

$\displaystyle (A+2I)v=0$

$\displaystyle \begin{pmatrix}1&3&1\\[1.1ex] 0&4&0\\[1.1ex] 3&-1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+3y+z = 0 \\[2ex] 4y = 0\\[2ex] 3x-y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] x = -z \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] -1\end{pmatrix}$

Berechnen wir nun die Eigenvektoren, die zu den Eigenwerten 2 gehören.

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}-3&3&1\\[1.1ex] 0&0&0\\[1.1ex] 3&-1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3x+3y+z = 0 \\[2ex] 0= 0\\[2ex] 3x-y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] z=3x \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 3\end{pmatrix}$

Da der Eigenwert 2 zweimal wiederholt wird, müssen wir einen weiteren Eigenvektor berechnen, der die Unterraumgleichungen (oder Eigenraumgleichungen) erfüllt:

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] -3\end{pmatrix}$

Wir bauen die Matrix

$P$

, gebildet durch die drei Eigenvektoren der Matrix:

$\displaystyle P = \begin{pmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{pmatrix}$

Allerdings sind die drei Vektoren nicht linear unabhängig, da offensichtlich die beiden Eigenvektoren mit Eigenwert 2 eine Linearkombination voneinander sind. Dies kann auch aufgrund der Determinante der Matrix nachgewiesen werden

$P$

ist gleich 0 (hat eine Zeile voller Nullen):

$\displaystyle \text{det}(P) = \begin{vmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{vmatrix}=0$

Da die Eigenvektoren linear abhängig sind, ist die Matrix A daher nicht diagonalisierbar .

Übung 5

Wenn möglich, diagonalisieren Sie die folgende quadratische Matrix der Größe 3×3:

$\displaystyle A= \begin{pmatrix}3&0&0\\[1.1ex] 0&2&1\\[1.1ex] 0&1&2\end{pmatrix}$

Sehen Sie sich die Lösung an

Der erste Schritt besteht darin, die Eigenwerte der Matrix A zu finden. Wir berechnen daher die charakteristische Gleichung, indem wir die Determinante der folgenden Matrix lösen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}$

Da die erste Zeile bis auf 3 vollständig aus Nullen besteht, nutzen wir dies, um die Determinante der Matrix durch Cofaktoren (oder Adjungierte) zu lösen:

$\displaystyle \begin{aligned} \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}& = (3-\lambda)\cdot \begin{vmatrix} 2-\lambda&1\\[1.1ex]1&2-\lambda \end{vmatrix} \\[3ex] & = (3-\lambda)[\lambda^2 -4\lambda +3] \end{aligned}$

Wir müssen nun die Wurzeln des charakteristischen Polynoms berechnen. Es ist besser, die Klammern nicht zu multiplizieren, da man dann ein Polynom dritten Grades erhalten würde. Werden die beiden Faktoren hingegen getrennt gelöst, ist es einfacher, die Eigenwerte zu erhalten:

$\displaystyle (3-\lambda)[\lambda^2 -4\lambda +3]=0 \ \longrightarrow \ \begin{cases} 3-\lambda=0 \ \longrightarrow \ \lambda = 3 \\[2ex] \lambda^2 -4\lambda +3=0 \ \longrightarrow \begin{cases}\lambda = 1 \\[2ex] \lambda = 3 \end{cases} \end{cases}$

Die Eigenwerte der Matrix sind also:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 3$

Sobald die Eigenwerte gefunden wurden, berechnen wir den zu jedem von ihnen zugehörigen Eigenvektor. Zunächst der Eigenvektor, der dem Eigenwert 1 entspricht:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}2&0&0\\[1.1ex] 0&1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2x = 0 \\[2ex] y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=0 \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

Dann berechnen wir die zu den Eigenwerten 3 gehörenden Eigenvektoren:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}0&0&0\\[1.1ex] 0&-1&1\\[1.1ex] 0&1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 0 = 0 \\[2ex] -y+z = 0\\[2ex] y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 1 \\[1.1ex] 1\end{pmatrix}$

Da der Eigenwert 3 zweimal wiederholt wird, müssen wir einen weiteren Eigenvektor berechnen, der die Eigenraumgleichungen erfüllt:

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

Wir bauen die Matrix

$P$

, gebildet durch die Eigenvektoren der Matrix:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}$

Im Gegensatz zu Aufgabe 4 konnten wir in diesem Fall drei linear unabhängige Vektoren bilden, obwohl die algebraische Vielfachheit des Eigenwerts 3 doppelt so groß ist. Dies kann anhand der Determinante der Matrix überprüft werden

$P$

ergibt ein von 0 verschiedenes Ergebnis:

$\displaystyle \text{det}(P) = \begin{vmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{vmatrix} =-2 \neq 0$

Damit können wir die Diagonalzerlegung der Matrix A durchführen. Und die entsprechende Diagonalmatrix ist diejenige, die die Eigenwerte auf der Hauptdiagonale hat:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Denken Sie daran, dass die Eigenwerte in derselben Reihenfolge platziert werden müssen, in der die Eigenvektoren in der Matrix platziert werden

$P$

Kurz gesagt, die Basisänderungsmatrix, die zur Diagonalisierung der Matrix und ihrer diagonalisierten Form erforderlich ist, sind:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}\qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Übung 6

Führen Sie, wenn möglich, die Diagonalisierung der folgenden Matrix der Dimension 4×4 durch:

$\displaystyle A=\begin{pmatrix}2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Sehen Sie sich die Lösung an

Der erste Schritt besteht darin, die Eigenwerte der Matrix A zu finden. Wir berechnen daher die charakteristische Gleichung, indem wir die Determinante der folgenden Matrix lösen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}$

In diesem Fall besteht die letzte Spalte der Determinante bis auf ein Element nur aus Nullen. Wir werden dies daher nutzen, um die Determinante anhand von Cofaktoren über diese Spalte zu berechnen:

$\displaystyle \begin{aligned} \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}& = (5-\lambda)\cdot \begin{vmatrix}2-\lambda&1&2\\[1.1ex] 1&-3-\lambda&1\\[1.1ex] 0&-1&-\lambda\end{vmatrix}\\[3ex] & = (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda] \end{aligned}$

Wir müssen nun die Wurzeln des charakteristischen Polynoms berechnen. Auf das Produkt der Klammern sollte besser verzichtet werden, da man dann ein Polynom vierten Grades erhalten würde. Wenn die beiden Faktoren jedoch getrennt gelöst werden, ist es einfacher, die Eigenwerte zu berechnen:

$\displaystyle (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda]=0 \ \longrightarrow \ \begin{cases} 5-\lambda=0 \ \longrightarrow \ \lambda = 5 \\[2ex] -\lambda^3 -\lambda^2 +6\lambda =0 \ \longrightarrow \ \lambda(-\lambda^2 -\lambda +6) =0 \end{cases}$

$\displaystyle \lambda(-\lambda^2 -\lambda +6)=0 \ \longrightarrow \ \begin{cases} \lambda=0 \\[2ex] -\lambda^2 -\lambda +6=0 \ \longrightarrow \ \begin{cases} \lambda=2 \\[2ex] \lambda = -3 \end{cases}\end{cases}$

Die Eigenwerte der Matrix sind also:

$\lambda=0 \qquad \lambda =-3 \qquad \lambda = 2\qquad \lambda = 5$

Sobald alle Eigenwerte gefunden sind, gehen wir zu den Eigenvektoren über. Wir berechnen den Eigenvektor zum Eigenwert 0:

$\displaystyle (A-0I)v=0$

$\displaystyle \begin{pmatrix} 2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2w+x+2y = 0 \\[2ex] w-3x+y = 0\\[2ex] -x=0 \\[2ex] 5z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=0 \\[2ex] z=0 \\[2ex]w=-y \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Wir berechnen den Eigenvektor zum Eigenwert -3:

$\displaystyle (A+3I)v=0$

$\displaystyle \begin{pmatrix} 5&1&2&0\\[1.1ex] 1&0&1&0\\[1.1ex] 0&-1&3&0\\[1.1ex] 0&0&0&8\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 5w+x+2y = 0 \\[2ex] w+y = 0\\[2ex] -x+3y=0 \\[2ex] 8z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=-y \\[2ex]x=3y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 3 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Wir berechnen den Eigenvektor zum Eigenwert 2:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix} 0&1&2&0\\[1.1ex] 1&-5&1&0\\[1.1ex] 0&-1&-2&0\\[1.1ex] 0&0&0&3\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] w-5x+y = 0\\[2ex] -x-2y=0 \\[2ex] 3z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=-2y \\[2ex] w=-11y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-11 \\[1.1ex] -2 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Wir berechnen den Eigenvektor zum Eigenwert 5:

$\displaystyle (A-5I)v=0$

$\displaystyle \begin{pmatrix} -3&1&2&0\\[1.1ex] 1&-8&1&0\\[1.1ex] 0&-1&-5&0\\[1.1ex] 0&0&0&0\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3w+x+2y = 0 \\[2ex] w-8x+y = 0\\[2ex] -x-5y=0 \\[2ex] 0=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=x=y=0 \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0 \\[1.1ex]1 \end{pmatrix}$

Wir erstellen die Matrix

$P$

, zusammengesetzt aus den Eigenvektoren der Matrix:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix}$

Da alle Eigenwerte voneinander verschieden sind, ist Matrix A diagonalisierbar. Somit ist die entsprechende Diagonalmatrix diejenige, deren Eigenwerte auf der Hauptdiagonale liegen:

$\displaystyle D= \begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Denken Sie daran, dass die Eigenwerte in derselben Reihenfolge platziert werden müssen, in der die Eigenvektoren in der Matrix positioniert sind

$P$

Zusammenfassend sind die grundlegenden Matrixänderungen, die zur Diagonalisierung der Matrix A und der Matrix in Diagonalform erforderlich sind:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix} \qquad D=\begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Anwendungen diagonalisierbarer Matrizen

Wenn Sie es bis hierher geschafft haben, fragen Sie sich wahrscheinlich: Wozu dient eine diagonalisierbare Matrix?

Nun, diagonalisierbare Matrizen sind sehr nützlich und werden in der Mathematik häufig verwendet. Der Grund dafür ist, dass eine Diagonalmatrix praktisch voller Nullen ist und daher Berechnungen viel einfacher macht.

Ein klares Beispiel hierfür sind die Potenzen diagonalisierbarer Matrizen, deren Ergebnis durch die folgende Formel vereinfacht wird:

$\displaystyle A^k=PD^kP^{-1}$

Diese Gleichheit lässt sich leicht durch Induktion beweisen. Es reicht daher aus, die Matrix anzuheben

$D$

an den Aussteller. Und da es sich um eine Diagonalmatrix handelt, reduziert sich die Operation darauf, jeden Term der Hauptdiagonale auf den Exponenten zu erhöhen:

$\displaystyle D^k = diag(\lambda_1^k,\lambda_2^k, \ldots , \lambda_n^k)$

Beispiel für die Potenz einer diagonalisierbaren Matrix

Zum besseren Verständnis berechnen wir als Beispiel die Potenz einer diagonalisierbaren Matrix:

$\displaystyle A= \begin{pmatrix}2&0\\[1.1ex] 3&1\end{pmatrix}$

Die grundlegende Veränderungsmatrix

$P$

, gebildet durch seine Eigenvektoren und die diagonalisierte Matrix

$D$

, bestehend aus seinen eigenen Werten, sind:

$\displaystyle P = \begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}$

Um ein Beispiel zu nennen: Die auf 7 erhöhte Matrix A entspricht:

$\displaystyle A^7=PD^7P^{-1}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\left.\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\right.^{-1}$

Jetzt invertieren wir die Matrix

$P:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

Wir lösen nach der Potenz der Matrix

$D:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1^7&0\\[1.1ex] 0&2^7\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&128\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

Und schließlich führen wir die Multiplikationen der Matrizen durch:

$\displaystyle \bm{A^7=}\begin{pmatrix}\bm{128}&\bm{0}\\[1.1ex] \bm{381}&\bm{1}\end{pmatrix}$

Wie Sie gesehen haben, ist es bequemer, die Potenz mit einer Diagonalmatrix zu berechnen, als dieselbe Matrix siebenmal hintereinander zu multiplizieren. Stellen Sie sich das dann mit viel größeren Exponentenwerten vor.

Eigenschaften diagonalisierbarer Matrizen

Die Merkmale dieses Matrixtyps sind:

Wenn die Matrix
$A$

ist diagonalisierbar, jede Potenz von

$A$

.

Fast alle Matrizen können in einer komplexen Umgebung diagonalisiert werden
$\mathbb{C}$

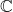
. Allerdings gibt es unten die Ausnahmen, die niemals diagonalisierbar sind.

Wenn die Matrix
$P$

ist eine orthogonale Matrix, dann sagen wir, dass die Matrix

$A$

ist orthogonal diagonalisierbar und daher kann die Gleichung umgeschrieben werden:

$\displaystyle A=PDP^t$

Eine Matrix ist genau dann durch eine Einheitsmatrix diagonalisierbar, wenn es sich um eine Normalmatrix handelt.

Gegeben zwei diagonalisierbare Matrizen sind sie genau dann kommutierbar, wenn sie gleichzeitig diagonalisiert werden können, das heißt, wenn sie dieselbe orthonormale Basis von Eigenvektoren (oder Eigenvektoren) haben.

Wenn ein Endomorphismus diagonalisierbar ist, sagen wir, dass er durch Ähnlichkeit diagonalisierbar ist. Allerdings sind nicht alle Endomorphismen diagonalisierbar, oder mit anderen Worten, die Diagonalisierung eines Endomorphismus ist nicht gewährleistet.

Simultane Diagonalisierung

Eine Menge von Matrizen heißt gleichzeitig diagonalisierbar, wenn es eine invertierbare Matrix gibt, die als Grundlage für die Diagonalisierung einer beliebigen Matrix in dieser Menge dient. Mit anderen Worten: Wenn zwei Matrizen auf derselben Eigenvektorbasis diagonalisieren, bedeutet dies, dass sie gleichzeitig diagonalisierbar sind.

Darüber hinaus müssen, wie wir in den Eigenschaften der Matrixdiagonalisierung erläutert haben, zwei Matrizen miteinander kommutieren, wenn sie gleichzeitig diagonalisieren können.

Beispielsweise sind die folgenden beiden Matrizen kommutierbar, sodass sie auf der gleichen Basis von Eigenvektoren oder Eigenvektoren diagonalisieren.

$\displaystyle A=\begin{pmatrix}2&0 \\[1.1ex] 1&-1 \end{pmatrix} \qquad B=\begin{pmatrix}3&0\\[1.1ex] 1&0 \end{pmatrix}$

Selbst wenn sie dieselben Eigenvektoren haben, bedeutet das nicht, dass sie dieselben Eigenwerte haben. Obwohl die obigen Matrizen A und B ähnliche Eigenvektoren haben, haben sie tatsächlich unterschiedliche Eigenwerte.

Nicht diagonalisierbare Matrizen

Obwohl die überwiegende Mehrheit der Matrizen in einer Umgebung mit komplexen Zahlen diagonalisierbar ist, können einige Matrizen niemals diagonalisiert werden.

Diese Tatsache tritt auf, wenn die algebraische Multiplizität eines Eigenwerts (oder Eigenwerts) nicht mit der geometrischen Multiplizität übereinstimmt.

Beispielsweise kann die folgende Matrix in keiner Weise diagonalisiert werden, sie ist „indiagonalisierbar“:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] 0&0 \end{pmatrix}$

Darüber hinaus gibt es Matrizen, die in einer Umgebung mit reellen Zahlen nicht diagonalisieren können, bei der Arbeit mit komplexen Zahlen jedoch diagonalisieren, wie diese Matrix:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] -1&0 \end{pmatrix}$

Schließlich gibt es einige Matrixblockdiagonalisierungsverfahren , die nicht rein diagonalisierbar, sondern etwas komplizierter sind. Die bekannteste Methode ist die Diagonalisierung mit der kanonischen Form von Jordan .

Diagonalisieren Sie eine Matrix mit MATLAB

Computerprogramme sind sehr praktisch, wenn es um die Diagonalisierung von Matrizen geht, insbesondere wenn diese sehr groß sind. Und die bekannteste Software ist sicherlich MATLAB . Als nächstes werden wir sehen, wie man mit diesem Programm eine Matrix diagonal faktorisiert.

Die Anweisung zur Diagonalisierung einer Matrix mit MATLAB lautet:

$\displaystyle \text{[P, D] = eig(A)}$

Gold

$A$

ist die zu diagonalisierende Matrix und

$P$

Und

$D$

sind die Matrizen, die das Programm zurückgibt:

$P$

ist die durch die Eigenvektoren und gebildete Matrix

$D$

ist die Matrix in Diagonalform, deren Hauptdiagonalterme die Eigenwerte sind.

Daher müssen Sie diesen Code nur in das Programm eingeben.

Wenn Sie hingegen nur die Eigenwerte wissen möchten, können Sie die folgende Aussage verwenden:

$\displaystyle e= eig(A)}$

Gold

$e$

ist der Spaltenvektor, den MATLAB mit den Eigenwerten der Matrix zurückgibt

$A$

So diagonalisieren sie eine matrix

Was ist eine diagonalisierbare Matrix?

Wann kann man eine Matrix diagonalisieren?

So diagonalisieren Sie eine Matrix

Übungen zur Matrixdiagonalisierung gelöst

Übung 1

Übung 2

Übung 3

Übung 4

Übung 5

Übung 6

Anwendungen diagonalisierbarer Matrizen

Beispiel für die Potenz einer diagonalisierbaren Matrix

Eigenschaften diagonalisierbarer Matrizen

Simultane Diagonalisierung

Nicht diagonalisierbare Matrizen

Diagonalisieren Sie eine Matrix mit MATLAB

Kommentar verfassen Kommentieren abbrechen