Was sind Vektoren (Mathematik)? -Mathorität

Auf dieser Seite finden Sie alles über Vektoren: Was sie sind, ihre Eigenschaften, wie sie berechnet werden, wie man Operationen mit Vektoren durchführt, welche verschiedenen Typen es gibt, …

Was ist ein Vektor?

Die mathematische Definition eines Vektors lautet wie folgt:

In der Mathematik ist ein Vektor ein gerichtetes Segment, das von einem Punkt (genannt Ursprung) zu einem anderen Punkt (genannt Ende) verläuft.

In der folgenden Grafik können Sie beispielsweise sehen, dass der Vektor

$\vv{AB}$

Es hat Punkt A als Ursprung und Punkt B als Endpunkt.

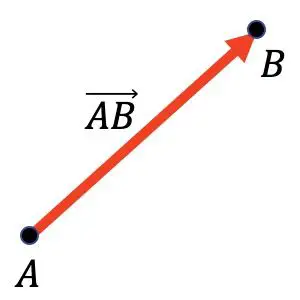
Vektoren werden hauptsächlich in der Mathematik, insbesondere der Geometrie und der Physik, verwendet, um Vektorkräfte grafisch darzustellen.

Eigenschaften eines Vektors

Nachdem wir die mathematische Bedeutung von Vektoren kennengelernt haben, wollen wir uns nun mit ihren Eigenschaften befassen.

Jeder Vektor hat die folgenden geometrischen Eigenschaften:

Richtung : Die Richtung eines Vektors ist die Richtung der Linie, die den Vektor enthält, oder einer dazu parallelen Linie. Mit anderen Worten: Die Richtung eines Vektors ist die Linie, auf der er liegt.
Richtung : Die Richtung eines Vektors ist die Ausrichtung dieses Vektors, angezeigt durch seinen Pfeil.
Modul (oder Betrag): Der Modul eines Vektors ist seine Länge und entspricht dem numerischen Wert des Vektors. Je größer der Vektor bedeutet, desto größer ist daher die Vektormenge, die er darstellt.
Anwendungspunkt : Der Anwendungspunkt eines Vektors ist der Ursprung dieses Vektors.

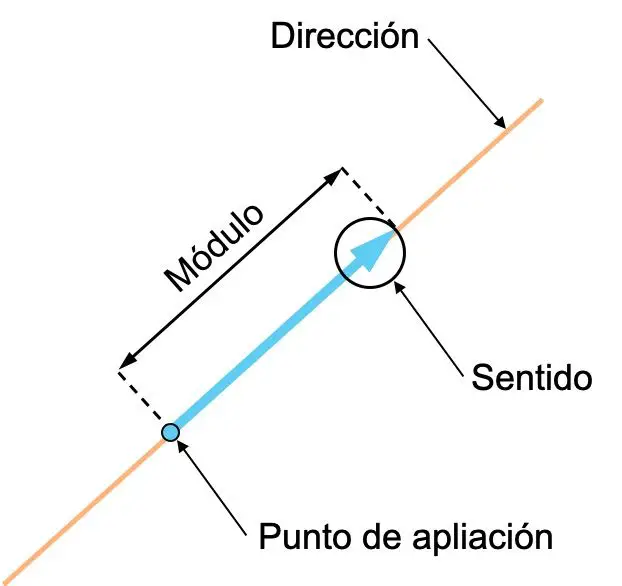
Die Begriffe „Richtung“ und „Richtung eines Vektors“ sind oft verwirrend, daher ist es wichtig, den Unterschied zwischen ihnen zu unterscheiden. Schauen Sie sich das folgende Beispiel mit zwei Vektoren an. Beide haben die gleiche Richtung, aber ihre Bedeutung ist unterschiedlich:

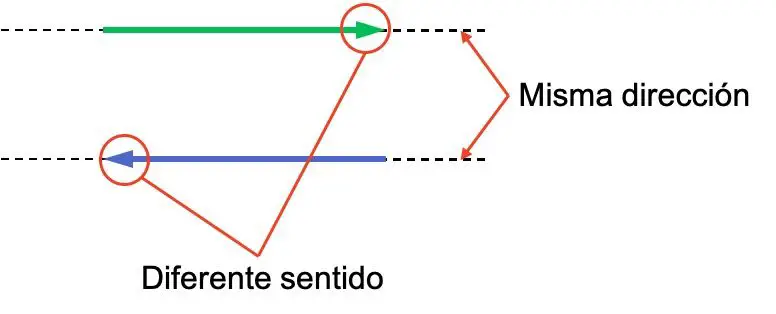
Bedeutung der Bedeutung und Richtung eines Vektors

Die beiden Vektoren haben die gleiche Richtung, weil sie parallel sind. Stattdessen sind ihre Richtungen entgegengesetzt, da sie nach hinten zeigen.

Komponenten eines Vektors

Wir haben gerade gesehen, dass Vektoren grafisch durch Pfeile dargestellt werden, Vektoren können aber auch numerisch durch die Komponenten (oder Koordinaten) eines Vektors dargestellt werden.

Wenn wir beispielsweise den folgenden Vektor in einem Diagramm darstellen:

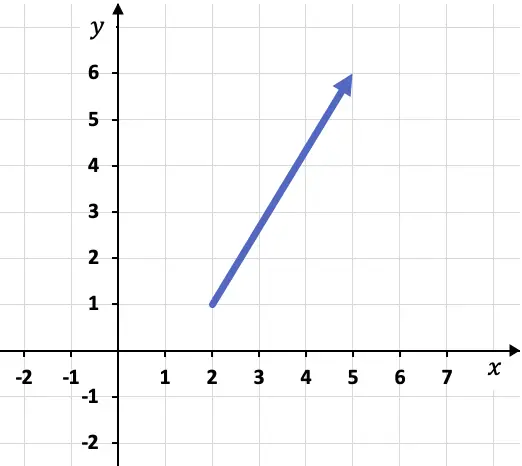
Um die Komponenten des Vektors zu berechnen, müssen wir zunächst die Koordinaten seines Ursprungs und Endes ermitteln, also die Punkte, an denen er beginnt und endet. In diesem Fall sind Ursprung und Ende des Vektors:

Ursprung des Vektors: A(2,1)

Endpunkt des Vektors: B(5,6)

Um also die Koordinaten oder Komponenten des Vektors zu finden, subtrahieren Sie einfach den Endpunkt minus den Ursprung:

$\begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}$

Damit sind die Komponenten des im Diagramm dargestellten Vektors:

$\vv{\bm{AB}}\bm{=(3,5)}$

Vektoroperationen

Vektor hinzufügen

Um zwei Vektoren numerisch zu addieren, müssen Sie ihre jeweiligen Komponenten addieren. Mit anderen Worten: Die X-Koordinaten der beiden Vektoren werden addiert und stimmen mit den Y-Koordinaten überein.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y) \end{array} \end{empheq}$

Damit Sie sehen können, wie das geht, fügen wir die folgenden zwei Vektoren hinzu:

$\vv{\text{u}} = (2,3) \qquad \vv{\text{v}}=(4, -1)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}$

Zwei Vektoren können auch aus ihren grafischen Darstellungen hinzugefügt werden. Normalerweise wird hierfür die Parallelogrammregel oder das Parallelogrammgesetz verwendet, es gibt jedoch viele Methoden. Beispiele und gelöste Übungen zur grafischen Addition zweier Vektoren finden Sie hier.

Vektorsubtraktion

Um zwei Vektoren analytisch zu subtrahieren, müssen Sie ihre jeweiligen Komponenten subtrahieren. Das heißt, die X-Koordinaten der beiden Vektoren werden voneinander subtrahiert und stimmen mit den Y-Koordinaten überein.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y) \end{array} \end{empheq}$

Als Beispiel subtrahieren wir die folgenden zwei Vektoren:

$\vv{\text{u}} = (3,1) \qquad \vv{\text{v}}=(2, -4)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}$

Wie bei der Addition können Sie auch zwei Vektoren mithilfe ihrer Darstellungen subtrahieren. Hierfür wird üblicherweise die Dreiecksregel oder das Dreiecksgesetz verwendet, es gibt jedoch mehrere Methoden. Sie können sie alle mit Beispielen und gelösten Übungen zur grafischen Subtraktion zweier Vektoren sehen.

Modul eines Vektors

Wie wir am Anfang dieser Seite gesehen haben, entspricht die Größe eines Vektors der Länge dieses Vektors. Nun, die Länge (oder Größe) eines Vektors kann aus seinen Komponenten bestimmt werden.

Betrachten Sie einen beliebigen Vektor:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Um den Betrag eines Vektors in der Ebene zu ermitteln, müssen wir die folgende Formel anwenden:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2} \end{empheq}$

Wir berechnen beispielsweise den Betrag des folgenden Vektors mit der Formel:

$\vv{\text{u}} = (3,-4)$

$\lvert \vv{\text{u}} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{9+16}=\sqrt{25} = \bm{5}$

Obwohl es sehr einfach erscheint, kann die Bestimmung der Größe eines Vektors kompliziert sein. Wenn Sie weitere Beispiele sehen und mit gelösten Übungen des Moduls eines Vektors üben möchten, empfehlen wir Ihnen, diese verlinkte Seite zu besuchen.

Multiplikation eines Vektors mit einem Skalar

Um das Produkt eines Vektors mit einer Zahl (oder einem Skalar) numerisch zu berechnen, muss jede Komponente des Vektors mit dieser Zahl multipliziert werden.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}\vv{\text{u}} = (\text{u}_x,\text{u}_y)\\[4ex]k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y) \end{array} \end{empheq}$

Im folgenden generischen Beispiel können Sie sehen, wie die Richtung des Vektors unabhängig vom Vorzeichen des Skalars beibehalten wird. Andererseits hängt die Richtung des Vektors vom Vorzeichen der Zahl ab, die er multipliziert.

Multiplikation oder Produkt einer Zahl oder eines Skalars mit einem Vektor

Unten sehen Sie ein numerisches Beispiel, wie Sie das Produkt eines Vektors und einer Zahl ermitteln:

$\vv{\text{u}} =(3,-2)$

$4\cdot \vv{\text{u}} =(4 \cdot 3 \ , \ 4 \cdot (-2)) = \bm{(12,-8)}$

Skalarprodukt

In der analytischen Geometrie ist das Skalarprodukt eine Vektoroperation, die zwei Vektoren multipliziert und in eine reelle Zahl umwandelt.

Somit lautet die Formel für das Skalarprodukt zweier Vektoren wie folgt:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y \end{empheq}$

Unten sehen Sie ein Beispiel, in dem das Ergebnis des Skalarprodukts zwischen zwei Vektoren berechnet wird:

$\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,3)$

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}$

Unter diesem Link können Sie weitere Beispiele für das Skalarprodukt sehen. Darüber hinaus finden Sie eine weitere Möglichkeit, das Skalarprodukt zwischen zwei Vektoren zu finden, die Eigenschaften dieser Art von Operation mit Vektoren und Übungen, die Schritt für Schritt gelöst werden.

Vektorprodukt

Obwohl sie sich im Namen sehr ähneln, sind Skalarprodukt und Kreuzprodukt völlig unterschiedlich.

Kreuzprodukt , auch Kreuzprodukt genannt, ist eine Operation zwischen zwei Vektoren im Raum (im R3), das heißt, es handelt sich um Dreikoordinatenvektoren.

Wenn wir also zwei beliebige dreidimensionale Vektoren haben:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

Das Kreuzprodukt der beiden Vektoren ist gleich dem Ergebnis der folgenden 3×3-Determinante:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix} \end{empheq}$

wo die Vektoren

$\vv{i}, \vv{j},\vv{k}$

sind die Einheitsvektoren in den Richtungen der X-, Y- und Z-Achse.

Darüber hinaus ist die Richtung des resultierenden Vektors senkrecht zu den beiden multiplizierten Vektoren.

Wie Sie sich vorstellen können, ist die Lösung dieser Art von Operation schwieriger als die vorherigen. Aus diesem Grund haben wir eine ganze Seite mit einer detaillierten Erklärung, wie das Kreuzprodukt zwischen zwei Vektoren berechnet wird. Wenn Sie Interesse haben, empfehlen wir Ihnen daher, es zu besuchen und mit den gelösten Vektorproduktübungen zu üben.

gemischtes Produkt

Das gemischte Produkt dreier Vektoren, auch Dreifachskalarprodukt genannt, ist eine sukzessive Multiplikation zwischen drei Vektoren, die zwei verschiedene Arten von Operationen umfasst: das Skalarprodukt und das Vektorprodukt. Die Kombination der beiden Vektoroperationen ergibt also einen Skalar (eine reelle Zahl).

Konkret besteht das gemischte Produkt aus der Berechnung des Vektorprodukts zweier Vektoren und der anschließenden vektoriellen Multiplikation des erhaltenen Ergebnisses mit einem dritten Vektor. Schauen Sie sich die Formel an:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.3pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}}) \end{empheq}$

Wie beim Vektorprodukt ist die Lösung des gemischten Produkts zwischen Vektoren nicht einfach. Aus diesem Grund empfehlen wir Ihnen, einen Blick auf diese Erklärung zum gemischten Produkt dreier Vektoren zu werfen, in der Sie Beispiele, gelöste Aufgaben und die geometrische Bedeutung dieser Vektoroperation finden.

Vektortypen

Es gibt viele verschiedene Arten von Vektoren, aber die wichtigsten Definitionen, die Sie kennen sollten, sind:

Einheitsvektor : Vektor, dessen Modul gleich 1 ist.
Fester Vektor : Ein Vektor ist fest, wenn der Ursprung des Vektors auf einen festen Punkt angewendet wird.
Freier Vektor : Ein Vektor ist frei, wenn sein Angriffspunkt nicht definiert ist, aber ein freier Punkt ist.
Kollineare Vektoren : Zwei oder mehr Vektoren sind kollinear, wenn sie dieselbe Wirkungslinie haben (Linie, auf der sich der Vektor befindet).
Äquivalente Vektoren : Zwei Vektoren sind äquivalent, wenn sie die gleiche Größe, den gleichen Sinn und die gleiche Richtung haben (obwohl sie unterschiedliche Angriffspunkte haben können).
Verknüpfte Vektoren : Verknüpfte Vektoren sind äquivalente Vektoren, die ebenfalls auf derselben Linie wirken.
Entgegengesetzte Vektoren : Zwei Vektoren sind entgegengesetzt, wenn sie den gleichen Betrag und die gleiche Richtung, aber eine unterschiedliche Richtung haben.
Positionsvektor : Der Positionsvektor ist der Vektor, dessen Ursprung der Punkt (0,0) (Ursprung der Koordinaten) ist.
Konkurrierende Vektoren : Zwei oder mehr Vektoren sind gleichzeitig, wenn ihre Wirkungslinien durch denselben Punkt verlaufen, sich also schneiden.
Parallele Vektoren : Zwei oder mehr Vektoren sind parallel, wenn sie unabhängig von ihrer Richtung die gleiche Richtung haben.
Senkrechte Vektoren : Zwei Vektoren sind senkrecht (oder orthogonal), wenn ihre Richtungen einen Winkel von 90° bilden.
Orthonormale Vektoren : Zwei oder mehr Vektoren sind orthonormal, wenn sie senkrecht zueinander stehen und darüber hinaus einheitlich sind (ihr Betrag ist gleich eins).
Koplanare Vektoren : Zwei oder mehr Vektoren sind koplanar, wenn sie in derselben Ebene liegen.

Winkel zwischen zwei Vektoren

Um den Winkel zwischen zwei gegebenen Vektoren zu ermitteln, müssen wir die folgende Formel anwenden:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Gold

$\lvert \vv{\text{u}} \rvert$

Und

$\lvert \vv{\text{v}} \rvert$

sind die Module der Vektoren

$\vv{\text{u}}$

Und

$\vv{\text{v}}$

jeweils.

Was sind vektoren (mathematik)?