Auf dieser Seite finden Sie eine Erklärung zu den Komponenten (oder Koordinaten) eines Vektors. Außerdem können Sie sehen, wie sie aus zwei Punkten berechnet werden und wie sie durch ihr Modul und ihren Winkel zerlegt werden. Darüber hinaus finden Sie Beispiele und Schritt für Schritt gelöste Übungen.
Aus welchen Komponenten besteht ein Vektor?
Die Komponenten eines Vektors sind die Projektionen eines Vektors auf die kartesischen Achsen. Daher ist die Projektion des Vektors auf die x-Achse die X-Komponente des Vektors und entsprechend ist die Projektion des Vektors auf die y-Achse die Y-Komponente des Vektors.
Die Komponenten eines Vektors können auch als Koordinaten eines Vektors bezeichnet werden.
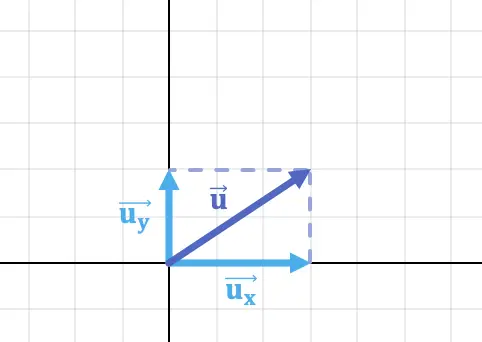
Die horizontale Komponente und die vertikale Komponente des Vektors im Bild oben sind beispielsweise:
![]()
![]()
Der Vektor ist also:
![]()
Daher können die Komponenten eines Vektors auch als Darstellung eines Vektors in einem Koordinatensystem definiert werden. Wenn es sich um ein zweidimensionales System (in r2) handelt, besteht der Vektor natürlich aus zwei Komponenten. Handelt es sich hingegen um eine dreidimensionale Basis (in r3), besteht der Vektor aus drei Komponenten.
Die kartesischen Komponenten eines Vektors sind so wichtig, weil wir mit ihnen die Eigenschaften des Vektors kennen können, bei denen es sich hauptsächlich um Richtung, Richtung und Modul (oder Betrag) des Vektors handelt. Darüber hinaus werden sie zur Durchführung von Vektoroperationen verwendet.
So berechnen Sie die Komponenten eines Vektors aus zwei Punkten
Wir haben gerade gesehen, wie man die Koordinaten eines Vektors grafisch ermittelt, wir können seine Komponenten jedoch auch numerisch bestimmen.
Um die Komponenten eines Vektors numerisch zu berechnen, müssen wir zwei Punkte kennen: seinen Ursprung und sein Ende, oder mit anderen Worten, wo er beginnt und wo er endet. Da die Komponenten eines Vektors die Koordinaten sind, die wir erhalten, indem wir sein Ende minus seinen Ursprung subtrahieren.
![]()
Zum Beispiel berechnen wir den Vektor, dessen Ursprung Punkt A(3,1) und dessen Ende Punkt B(5,4) ist:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{AB} & = (5,4)-(3,1) \\[1.5ex] &= (5-3,4-1) \\[1.5ex] & = \bm{(2,3)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4c740536015a29149532a4a1eb46f4f7_l3.png)
Wie Sie sehen, ist die Bestimmung der Komponenten eines Vektors nicht sehr schwierig, aber durchaus wichtig. Einer der am häufigsten verwendeten Vektortypen sind beispielsweise senkrechte (oder orthogonale) Vektoren; Wenn Sie die Koordinaten eines Vektors verstehen, ist es sehr einfach, senkrechte Vektoren zu berechnen. Wie das geht, können Sie in der Erklärung orthogonaler Vektoren sehen.
So berechnen Sie die Komponenten eines Vektors aus seinem Modul und Winkel
Sie können die Komponenten eines Vektors auch aus seiner Größe und dem Winkel ermitteln, den er mit der X-Achse bildet. Dieser Vorgang wird Vektorzerlegung genannt.
Somit können die X- und Y-Komponenten des Vektors mit den trigonometrischen Verhältnissen von Kosinus und Sinus berechnet werden:

Wie Sie im Bild sehen können, vervollständigt der Modul eines Vektors und seiner Komponenten ein rechtwinkliges Dreieck, sodass die Grundformeln der Trigonometrie angewendet werden können.
Wenn Sie sich nicht erinnern, wie der Modul eines Vektors berechnet wird, können Sie nachschlagen , wie hoch der Modul eines Vektors ist . Hier finden Sie die Formel für den Betrag eines Vektors, sowie Beispiele, Schritt-für-Schritt gelöste Aufgaben und alle Eigenschaften des Betrags eines Vektors. Dies ist eine sehr umfassende Erklärung, sodass Sie sie perfekt verstehen werden. ✅
Anders als der Betrag eines Vektors, der immer positiv ist, können seine Komponenten negativ sein, da Sinus und Cosinus negative Werte annehmen können.
Als Beispiel führen wir die Vektorzerlegung des Vektors durch, dessen Modul und Winkel mit der OX-Achse sind:
![]()
Die X-Komponente des Vektors ist gleich dem Modul multipliziert mit dem Kosinus des Winkels:
![]()
Und die Y-Komponente des Vektors ist gleich dem Produkt aus Modul und Sinus des Winkels:
![]()
Die Koordinaten des Vektors sind also:
![]()