Regelmäßige oder invertierbare Matrix

Auf dieser Seite finden Sie die Erklärung einer regulären oder invertierbaren Matrix und wie Sie wissen, wann die Inversion einer Matrix durchgeführt werden kann und wann nicht. Darüber hinaus sehen Sie auch mehrere Beispiele für reguläre Matrizen, um das Konzept vollständig zu verstehen, und schließlich zeigen wir Ihnen alle Eigenschaften dieses Matrixtyps.

Was ist eine reguläre Matrix?

Die Definition einer regulären Matrix lautet wie folgt:

Eine reguläre Matrix ist eine quadratische Matrix, die invertiert werden kann, d. h. die Umkehrung dieser Matrix kann berechnet werden. Daher ist seine Determinante ungleich Null (0).

Reguläre Matrizen werden auch als invertierbare, nicht singuläre oder nicht entartete Matrizen bezeichnet.

Die Gegenmatrix zur regulären Matrix ist die singuläre oder entartete Matrix.

Um also zu wissen, wann eine Matrix regelmäßig oder singulär ist, also wann eine Matrix invertierbar ist oder nicht, reicht es aus, die Determinante der Matrix zu lösen:

Wenn die Determinante der Matrix ungleich Null ist, ist die Matrix regelmäßig oder invertierbar.

Wenn die Determinante der Matrix gleich Null ist, ist die Matrix singulär oder nicht invertierbar.

Zusammenfassend lässt sich sagen, dass die Berechnung der Determinante einer Matrix der einfachste Weg ist, um herauszufinden, ob die Matrix eine Umkehrung hat oder nicht. Daher empfehlen wir dies, um die Invertibilität einer Matrix zu bestimmen.

Wenn Sie wissen möchten, wie man eine Matrix invertiert, können Sie sich die Formel für die inverse Matrix ansehen, die Schritt für Schritt erklärt, wie man eine Matrix invertiert. Außerdem finden Sie dort mehrere Beispiele und gelöste Übungen zum Üben.

Beispiele für reguläre oder invertierbare Matrizen

Nachdem wir die Bedeutung einer regulären oder invertierbaren Matrix verstanden haben, sehen wir uns einige Beispiele für reguläre Matrizen unterschiedlicher Dimensionen an:

Beispiel einer regulären oder invertierbaren 2×2-Matrix

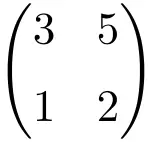
Wir können überprüfen, ob es sich um eine reguläre Matrix handelt, indem wir ihre Determinante berechnen:

$\displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}$

Die Determinante der Matrix der Ordnung 2 unterscheidet sich von 0, es handelt sich also um eine reguläre Matrix.

Beispiel einer regulären oder invertierbaren 3×3-Matrix

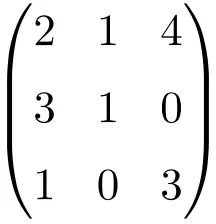
Beispiel einer regulären oder invertierbaren Matrix der Dimension 3x3

Wir müssen die Determinante der Matrix bestimmen, um zu überprüfen, ob es sich um eine invertierbare Matrix handelt:

$\displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}$

Die Determinante der Matrix der Ordnung 3 liefert ein anderes Ergebnis als 0, es handelt sich also um eine reguläre Matrix.

Beispiel einer regulären oder invertierbaren 4×4-Matrix

Beispiel einer regulären oder invertierbaren Matrix der Dimension 4x4

Die Bestimmung der Determinante der Matrix zeigt, dass es sich um eine reguläre Matrix handelt:

$\displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}$

Die Determinante der Matrix 4. Ordnung ist nicht Null, es handelt sich also um eine invertierbare Matrix.

Warnung: Wenn Sie Zweifel an der Berechnung von Determinanten haben, können Sie die Seite zur Berechnung einer Determinante konsultieren.

Eigenschaften regulärer oder invertierbarer Matrizen

Reguläre oder invertierbare Matrizen sind für die lineare Algebra sehr wichtig, und das liegt an den folgenden Eigenschaften:

Wenn A eine invertierbare Matrix ist, ist dies auch ihre transponierte oder transponierte Matrix. Darüber hinaus ist die inverse Matrix der Transponierten gleich der Transponierten der Inversen.

$\displaystyle \left(A^t\right)^{-1}=\left(A^{-1}\right)^t$

Der Bereich einer regulären Matrix ist immer der maximal mögliche, oder mit anderen Worten, der Bereich entspricht der Dimension der Matrix.

Das Matrixprodukt zwischen zwei invertierbaren Matrizen führt zu einer weiteren regulären Matrix. Diese Bedingung lässt sich leicht anhand der Eigenschaften der Determinanten nachweisen:

$\displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0$

Jede orthogonale Matrix ist gleichzeitig eine reguläre Matrix.

Sei A die Matrix, die ein System linearer Gleichungen darstellt
$(Ax=b)$

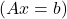
Wenn A eine reguläre Matrix ist, hat das System eine eindeutige Lösung und ist daher ein kompatibles Determinantensystem (SCD).

Darüber hinaus, wenn das System ein homogenes System ist
$(Ax=0)$

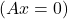
und A invertiert werden kann, ist die Lösung des Systems trivial:

$x=0.$

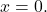
Die Spalten und Zeilen einer regulären Matrix sind linear unabhängig voneinander.

Alle Eigenwerte (oder Eigenwerte) einer regulären oder invertierbaren Matrix sind ungleich Null.

Regelmäßige umkehrbare goldmatrix