In diesem Artikel werden wir die Konzepte besprechen, die notwendig sind, um zu verstehen, was ein vollständiges Polynom ist. Darüber hinaus erfahren wir, wie es verwendet wird und warum es eine so wichtige Idee für die Manipulation und Quantifizierung von Polynomen ist. Zunächst wird jedoch dringend empfohlen, unseren Artikel über das Polynom zu lesen.
Was ist ein vollständiges Polynom?
Ein vollständiges Polynom ist ein algebraischer Ausdruck , der aus einer Summe von Termen besteht. Jeder Term wird durch Multiplikation einer Zahl, Koeffizient genannt, mit einer Potenz von x gebildet. Die höchste Potenz im Polynom wird als Grad des Polynoms bezeichnet, und die niedrigste (auf Null angehobenes x) wird als unabhängiger Term bezeichnet.
Von hier aus definieren wir ein vollständiges Polynom als eines, das Terme aller möglichen Grade bis zum Grad des Polynoms enthält. Mit anderen Worten: Wenn ein Polynom den Grad 5 hat, muss es Terme vom Grad 5, 4, 3, 2, 1 und 0 enthalten. Mit anderen Worten: Ein vollständiges Polynom ist eines, das keine Nullterme (gleich Null) hat ).
Im folgenden Bild sehen Sie ein Beispiel hierfür. Wie man sehen kann, gibt es für jeden Exponenten von x einen Term von x hoch vier (vier ist der Grad des Polynoms) bis x hoch null im unabhängigen Term. Daher erfüllt dieses Polynom die Definition eines vollständigen Polynoms.
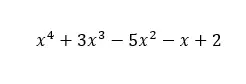
Wenn wir andererseits ein anderes Polynom wie das im folgenden Bild haben, haben wir es mit einem unvollständigen Polynom zu tun. Da zwei Terme fehlen, der von x auf zwei erhöht und der unabhängige Term. Und aus der Definition eines vollständigen Polynoms geht hervor, dass das Polynom nicht mehr vollständig ist, wenn auch nur ein Term fehlt.
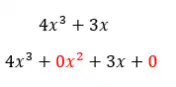
Beispiele für vollständige Polynome
Nachdem Sie nun die Definition des vollständigen Polynoms kennen, sehen wir uns einige Beispiele aus der Praxis an. Wir beginnen mit der Betrachtung eines vollständigen Polynoms vom Grad 2, eines weiteren vom Grad 4 und schließlich eines vom Grad 6. Natürlich könnten wir Beispiele für viel höhere Grade nennen, aber die Idee ist bei allen Arten von Polynomen dieselbe.
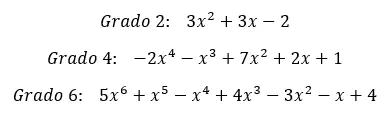
Anhand dieser Beispiele ist die Definition vollständiger Polynome sehr klar. Deshalb können wir jetzt zum nächsten Level übergehen. Im folgenden Abschnitt werden wir die beiden Arten vollständiger Polynome, die es gibt, entsprechend der Reihenfolge der Terme detailliert beschreiben. Das ist für viele Studierende eine Selbstverständlichkeit, aber es ist schön, es wieder zu sehen.
Arten vollständiger Polynome
Wir können vollständige Polynome in zwei Typen einteilen: geordnete vollständige Polynome und ungeordnete oder ungeordnete vollständige Polynome. Die ersten zeichnen sich durch eine Struktur aus, deren Terme nach den Graden von x geordnet sind . Beginnend mit dem höchsten Abschluss und endend mit dem Begriff „unabhängig“.
Obwohl es sich um ein vollständig ungeordnetes Polynom handelt, werden die Terme in zufälliger Reihenfolge ausgedrückt. Daher finden Sie den Term mit dem größten Exponenten neben dem unabhängigen Term. Da diese Art, ein Polynom auszudrücken, jedoch nicht praktikabel ist, empfehlen wir Ihnen, immer geordnete Polynome zu verwenden.
Als Nächstes zeigen wir Ihnen ein Beispiel für jeden Typ, damit Sie den Unterschied vollständig erkennen können.
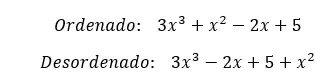
Wir hoffen, dass dieser Artikel Ihnen geholfen hat, das Konzept vollständiger Polynome zu verstehen. Wenn Sie Fragen haben, können Sie diese gerne in den Kommentaren hinterlassen.