Hier finden Sie die vertikalen Asymptoten einer Funktion (mit Beispielen). Außerdem erklären wir Ihnen, wie Sie die vertikalen Asymptoten einer Funktion ermitteln, und können zusätzlich anhand von Schritt für Schritt gelösten Übungen üben.
Was ist eine vertikale Asymptote?
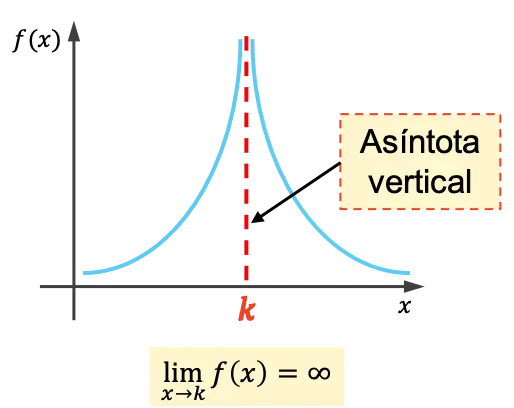
Eine vertikale Asymptote einer Funktion ist eine vertikale Linie, deren Graph sich auf unbestimmte Zeit annähert, ohne sie jemals zu kreuzen. Daher lautet die Gleichung für eine vertikale Asymptote x=k , wobei k der Wert der vertikalen Asymptote ist.
Das heißt, k ist eine vertikale Asymptote, wenn der Grenzwert der Funktion bei der Annäherung von x an k unendlich ist.
So berechnen Sie die vertikale Asymptote einer Funktion
Um die vertikale Asymptote einer Funktion zu berechnen, müssen die folgenden Schritte befolgt werden:
- Finden Sie den Definitionsbereich der Funktion. Liegen alle Punkte im Definitionsbereich, hat die Funktion keine vertikalen Asymptoten.
- Berechnen Sie den Grenzwert der Funktion an Punkten, die nicht im Definitionsbereich liegen.
- Die vertikalen Asymptoten der Funktion sind alle Werte, bei denen der Grenzwert Unendlich ergibt.
Beachten Sie, dass eine Funktion mehr als eine vertikale Asymptote haben kann. Beispielsweise hat der Graph der Tangensfunktion unendlich viele vertikale Asymptoten.
➤ Siehe: Eigenschaften der Tangensfunktion
Beispiel einer vertikalen Asymptote
Als Beispiel finden wir alle Asymptoten der folgenden rationalen Funktion, damit Sie sehen können, wie es gemacht wird:
![]()
Im Allgemeinen gehören Punkte mit vertikalen Asymptoten nicht zum Definitionsbereich der Funktion. Daher berechnen wir zunächst den Definitionsbereich der Funktion.
Da es sich um eine rationale Funktion handelt, schauen wir uns an, wann der Nenner verschwindet, um die Punkte zu bestimmen, die nicht zum Definitionsbereich gehören:
![]()
![]()
Daher umfasst der Definitionsbereich der Funktion alle reellen Zahlen außer x=2:
![]()
x=2 könnte also eine vertikale Asymptote der Funktion sein. Um dies zu überprüfen, müssen wir an dieser Stelle den Grenzwert der Funktion berechnen:
![]()
In diesem Fall haben wir die Unbestimmtheit einer Zahl zwischen Null erhalten und müssen daher zur Lösung des Grenzwerts die seitlichen Grenzen berechnen, um zu wissen, ob sie plus Unendlich oder minus Unendlich ist oder ob der Grenzwert nicht existiert. Wenn wir jedoch vertikale Asymptoten berechnen, müssen wir die seitlichen Grenzen nicht angeben, aber der Erhalt dieser Unbestimmtheit reicht aus, um zu sagen, dass es sich um eine vertikale Asymptote handelt.
Kurz gesagt, da der Grenzwert der Funktion bei Annäherung von x an 2 Unendlich ergibt, ist x=2 eine vertikale Asymptote.
Unten ist die Funktion grafisch dargestellt. Wie Sie sehen können, kommt sie der Geraden x=2 sehr nahe (sowohl von links als auch von rechts), schneidet sie jedoch nie, da es sich um eine vertikale Asymptote handelt:

Darüber hinaus können wir aus dem Diagramm die seitlichen Grenzen der Funktion am Punkt x=2 ableiten:
![]()
Probleme vertikaler Asymptoten gelöst
Übung 1
Berechnen Sie die vertikale Asymptote der folgenden rationalen Funktion:
![]()
Es gibt keine Formel zur Berechnung der vertikalen Asymptoten einer Funktion, aber Sie müssen den Definitionsbereich der Funktion finden und sehen, an welchen Punkten, an denen die Funktion nicht definiert ist, der Grenzwert Unendlich ergibt.
Daher setzen wir den Nenner der rationalen Funktion gleich 0, um die Punkte zu finden, die nicht zum Definitionsbereich gehören:
![]()
![]()
![]()
Somit umfasst der Definitionsbereich der Funktion alle reellen Zahlen außer x=1/2:
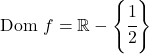
Also könnte x=1/2 eine vertikale Asymptote sein. Um dies zu überprüfen, berechnen wir an dieser Stelle den Grenzwert der Funktion:
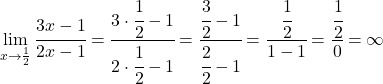
Also ist x=1/2 eine vertikale Asymptote , da der Grenzwert der Funktion an diesem Punkt Unendlich ergibt.
Übung 2
Finden Sie alle vertikalen Asymptoten der folgenden Bruchfunktion:
![]()
Zuerst setzen wir den Nenner des Bruchs gleich Null, um zu sehen, welche Werte nicht im Definitionsbereich der Funktion liegen:
![]()
Wir lösen die unvollständige quadratische Gleichung:
![]()
![]()
Der Definitionsbereich der rationalen Funktion ist daher:
![]()
Um also zu bestimmen, welche dieser beiden Werte vertikale Asymptoten sind, lösen wir an jedem Punkt nach dem Grenzwert der Funktion auf:
![]()
![]()
Die beiden Grenzwerte ergeben Unendlich, also sind x=3 und x=-3 die beiden vertikalen Asymptoten der Problemfunktion .
Übung 3
Finden Sie, falls vorhanden, alle vertikalen Asymptoten der folgenden rationalen Funktion:
![]()
➤ Siehe: Null-zwischen-Null-Unbestimmtheit
Zuerst lösen wir die quadratische Nennergleichung, um die Werte zu finden, die den Nenner des Bruchs aufheben:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle x&=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\cfrac{-2\pm\sqrt{2^2-4\cdot1\cdot(-3)}}{2\cdot1}=\\[3ex]\displaystyle &=\cfrac{-2\pm\sqrt{16}}{2}=\cfrac{-2\pm 4}{2}=\begin{cases}\cfrac{-2+4}{2}=1\\[3ex]\cfrac{-2-4}{2}=-3\end{cases}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9b2170358d5d1719077695aba5afa02e_l3.png)
Der Definitionsbereich der Funktion ist also:
![]()
Wir berechnen also zunächst den Grenzwert der Funktion bei x=1:
![]()
Und andererseits lösen wir den Grenzwert der Funktion, wenn x gegen -3 tendiert:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to -3}\frac{x+3}{x^2+2x-3}=\frac{-3+3}{(-3)^2+2\cdot(-3)-3}=\frac{0}{0}=\\[3ex]\displaystyle =\lim_{x \to -3}\frac{\cancel{x+3}}{(x-1)\cancel{(x+3)}}=\lim_{x \to -3}\frac{1}{x-1}=\frac{1}{-3-1}=-\frac{1}{4}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0e96a48986cd110e04058e3545290a0_l3.png)
Der vorherige Grenzwert gibt die unbestimmte Form Null zwischen Null an. Um ihn zu lösen, müssen wir die Polynome faktorisieren. Wenn Sie Zweifel daran haben, wie wir das Limit gelöst haben, finden Sie die vollständige Erklärung zur Lösung dieser Art von Unbestimmtheit im Link zur Übungserklärung.
In diesem Fall ergibt nur der Grenzwert der Funktion am Punkt x=1 Unendlich, sodass x=1 die einzige vertikale Asymptote der Funktion ist .