Vektorgleichung der Ebene

Auf dieser Seite finden Sie die Ebenenvektorgleichung (Formel) und Berechnungsbeispiele. Darüber hinaus können Sie anhand von Übungen und gelösten Problemen die Vektorgleichung der Ebene üben.

Wie lautet die Vektorgleichung einer Ebene?

In der analytischen Geometrie ist die Vektorgleichung einer Ebene eine Gleichung, die es ermöglicht, jede Ebene mathematisch auszudrücken. Um die Vektorgleichung einer Ebene zu finden, benötigen wir lediglich einen Punkt und zwei linear unabhängige Vektoren, die zu dieser Ebene gehören.

Formel der Vektorgleichung der Ebene

Betrachten Sie einen Punkt und zwei Richtungsvektoren einer Ebene:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

Die Formel für die Vektorgleichung einer Ebene lautet:

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Gold

$\lambda$

Und

$\mu$

sind zwei Skalare, also zwei reelle Zahlen.

Dies bedeutet also, dass jeder Punkt in einer Ebene als lineare Kombination aus einem Punkt und zwei Vektoren ausgedrückt werden kann.

Darüber hinaus ist eine notwendige Bedingung dafür, dass die vorherige Gleichung einer Ebene entspricht, dass die beiden Vektoren der Ebene lineare Unabhängigkeit haben, das heißt, die beiden Vektoren können nicht parallel zueinander sein. andere.

Bedenken Sie andererseits, dass es neben der Vektorgleichung auch andere Möglichkeiten gibt, eine Ebene analytisch auszudrücken, beispielsweise die parametrische Gleichung der Ebene und die implizite Gleichung der Ebene . Sie können in den Links überprüfen, um welche Art von Gleichung es sich handelt.

Beispiel, wie man die Vektorgleichung einer Ebene findet

Nachdem wir die Erklärung des Konzepts der Vektorgleichung der Ebene gesehen haben, sehen wir uns anhand eines Beispiels an, wie es berechnet wird:

Finden Sie die Vektorgleichung der Ebene, die durch den Punkt verläuft
$P(2,0,4)$

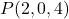
und enthält die Vektoren

$\vv{\text{u}}=(1,3,-2)$

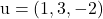
Und

$\vv{\text{v}}=(5,0,1).$

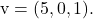
Um die Vektorgleichung der Ebene zu bestimmen, wenden Sie einfach ihre Formel an:

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

Und jetzt setzen wir den Punkt und jeden Vektor in die Gleichung ein:

$\bm{(x,y,z)=(2,0,4)+\lambda (1,3,-2) + \mu (5,0,1)}$

Wie Sie im Beispiel sehen können, ist es relativ einfach, die Vektorgleichung einer Ebene zu finden. Da die Aufgaben jedoch etwas komplizierter werden können, finden Sie im Folgenden mehrere gelöste Übungen mit unterschiedlichem Schwierigkeitsgrad, damit Sie sie üben können.

Probleme mit der Ebenenvektorgleichung gelöst

Übung 1

Bestimmen Sie die Vektorgleichung der Ebene, die den Vektor enthält

$\vv{\text{u}}=(0,-2,3)$

und geht dabei die folgenden zwei Punkte durch:

$A(1,3,-1)$

Und

$B(2,-1,5).$

siehe Lösung

Um die Gleichung einer Ebene zu kennen, braucht man einen Punkt und zwei Vektoren und in diesem Fall haben wir nur einen Vektor, wir müssen also einen anderen Richtungsvektor der Ebene finden. Dazu können wir den Vektor berechnen, der die beiden Punkte der Ebene definiert:

$\vv{AB} = B - A = (2,-1,5) - (1,3,-1) = (1,-4,6)$

Da wir nun bereits zwei Richtungsvektoren der Ebene und eines Punktes kennen, verwenden wir daher die Formel für die Vektorgleichung der Ebene:

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

Und wir setzen die beiden Vektoren und einen der beiden Punkte auf der Ebene in die Gleichung ein:

$\bm{(x,y,z)=(1,3,-1)+\lambda (0,-2,3) + \mu (1,-4,6)}$

Übung 2

Finden Sie die Vektorgleichung der Ebene, die die folgenden drei Punkte enthält:

$A(2,-2,1) \qquad B(1,0,4) \qquad C(-1,3,-2)$

siehe Lösung

Um die Vektorgleichung der Ebene zu finden, müssen wir zwei linear unabhängige Vektoren finden, die in der Ebene binden. Und dazu können wir zwei Vektoren berechnen, die durch die 3 Punkte definiert werden:

$\vv{AB} = B - A = (1,0,4) - (2,-2,1) = (-1,2,3)$

$\vv{AC} = C - A = (-1,3,-2) - (2,-2,1) = (-3,5,-3)$

Die Koordinaten der beiden gefundenen Vektoren sind nicht proportional, also linear unabhängig voneinander.

Nachdem wir nun bereits zwei Richtungsvektoren und einen Punkt der Ebene kennen, wenden wir daher die Formel für die Vektorgleichung der Ebene an:

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

Und wir setzen die beiden Vektoren und einen der drei Punkte der Ebene in die Gleichung ein:

$\bm{(x,y,z)=(2,-2,1)+\lambda (-1,2,3) + \mu (-3,5,-3)}$

Übung 3

Berechnen Sie 4 Punkte im Raum, die zu der durch die folgende Vektorgleichung definierten Ebene gehören:

$(x,y,z)=(0,2,1)+\lambda (2,-1,4) + \mu (-1,3,0)$

siehe Lösung

Um einen Punkt auf einer Ebene zu berechnen, geben Sie den Parametern einfach einen beliebigen Wert ein

$\lambda$

Und

$\mu .$

Noch:

$\left. \begin{array}{c} \lambda =0 \\[2ex] \mu =0 \end{array} \right\} \longrightarrow \ (0,2,1)+0\cdot (2,-1,4) + 0\cdot (-1,3,0)= \bm{(0,2,1)}$

$\left. \begin{array}{c} \lambda =1 \\[2ex] \mu =0 \end{array} \right\} \longrightarrow \ (0,2,1)+1\cdot (2,-1,4) + 0\cdot (-1,3,0)= \bm{(2,1,5)}$

$\left. \begin{array}{c} \lambda =0 \\[2ex] \mu =1 \end{array} \right\} \longrightarrow \ (0,2,1)+0\cdot (2,-1,4) + 1\cdot (-1,3,0)= \bm{(-1,5,1)}$

$\left. \begin{array}{c} \lambda =1 \\[2ex] \mu =1 \end{array} \right\} \longrightarrow \ (0,2,1)+1\cdot (2,-1,4) + 1\cdot (-1,3,0)= \bm{(1,4,5)}$

Übung 4

Finden Sie die Vektorgleichung der Ebene, die die Linie enthält

$r$

und ist parallel zur rechten Seite

$s.$

sind die Zeilen:

$\displaystyle r: \ \begin{cases} x=4+2t \\[1.7ex] y=-1+t\\[1.7ex] z=5-4t \end{cases} \qquad \qquad s: \ \frac{x-1}{2} = \frac{y+2}{4}= \frac{z+1}{-3}$

siehe Lösung

Um die Vektorgleichung der Ebene zu finden, müssen wir zwei Richtungsvektoren und einen Punkt dieser Ebene kennen. Die Anweisung sagt uns, dass sie die Zeile enthält

$r$

Daher können wir den Richtungsvektor und einen Punkt auf dieser Linie nehmen, um die Ebene zu definieren. Darüber hinaus sagt uns die Aussage, dass die Ebene parallel zur Geraden ist

$s,$