Vektorsubtraktion

Auf dieser Seite erfahren Sie, wie Sie zwei Vektoren sowohl grafisch als auch numerisch subtrahieren. Um sie grafisch zu subtrahieren, gibt es drei Methoden: das Parallelogramm, das Dreieck und das Polygon. Hier können Sie die Vor- und Nachteile der einzelnen Methoden unterscheiden. Darüber hinaus finden Sie Beispiele, Übungen und Schritt für Schritt gelöste Probleme.

Wie subtrahiere ich zwei Vektoren grafisch?

Es gibt mehrere Möglichkeiten, Vektoren geometrisch zu subtrahieren. Natürlich wird mit allen das gleiche Ergebnis erzielt, aber wir erklären Ihnen alle Methoden, damit Sie die Methode auswählen können, die Ihnen am besten gefällt. 👌

Um nur 2 Vektoren zu subtrahieren, gibt es zwei grafische Verfahren: die Parallelogrammmethode und die Dreiecksmethode . Wenn wir jedoch die Subtraktion von 3 oder mehr Vektoren lösen möchten, müssen wir die Polygonmethode verwenden.

Ohne weitere Umschweife finden Sie unten die Erklärungen zu all diesen Methoden.

Parallelogramm-Methode oder -Regel

Die Parallelogrammregel oder Parallelogrammmethode ist ein Verfahren, mit dem Sie auf sehr einfache Weise die Subtraktion zweier Vektoren durch ihre grafische Darstellung ermitteln können. Um diesen Prozess anzuwenden, müssen folgende Schritte ausgeführt werden:

1. Zuerst stellen wir die beiden Vektoren im Diagramm dar und positionieren sie am gleichen Anwendungspunkt, das heißt, wir platzieren die Ursprünge beider Vektoren am gleichen Punkt.
2. Zweitens zeichnen wir den entgegengesetzten Vektor des Vektors, der in der Operation subtrahiert wird, oder mit anderen Worten, wir kehren den Vektor um, der subtrahiert.
3. Dann zeichnen wir am Ende des hinzugefügten Vektors eine Linie parallel zum vorzeichengeänderten Vektor. Und wir wiederholen den Vorgang mit dem anderen Vektor. Damit erhalten wir die Zeichnung eines Parallelogramms (daher der Name der Regel).
4. Das Ergebnis der Subtraktion ist schließlich der Vektor, der vom gemeinsamen Ursprung der beiden Vektoren bis zum Schnittpunkt der beiden parallelen Linien verläuft.

Betrachten Sie das folgende allgemeine Beispiel, in dem zwei Vektoren mithilfe der Parallelogrammmethode subtrahiert werden:

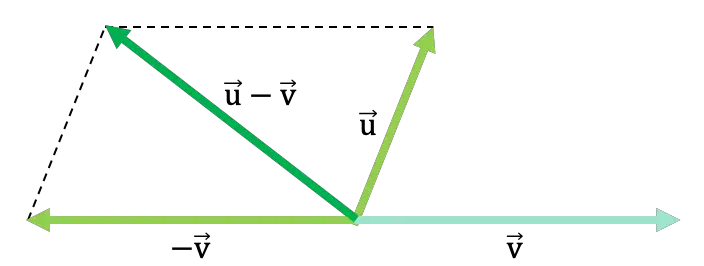
Dreiecksmethode oder -regel

Die Dreiecksmethode ist ein weiteres Verfahren, mit dem zwei Vektoren von ihrem Graphen subtrahiert werden können. In diesem Fall sind folgende Schritte zu befolgen:

1. Platzieren Sie die beiden Vektoren am gleichen Angriffspunkt, d. h. so, dass die beiden Vektoren denselben Ursprungspunkt haben.
2. Das Ergebnis der Vektorsubtraktion ist das Segment, das vom Ende des subtrahierenden Vektors bis zum Ende des anderen Vektors reicht. Wenn man genau hinschaut, wird ein Dreieck vervollständigt, indem die beiden Vektoren subtrahiert werden und der Vektor subtrahiert wird.

Hier ist ein Beispiel für die Vektorsubtraktion mit der Dreiecksmethode:

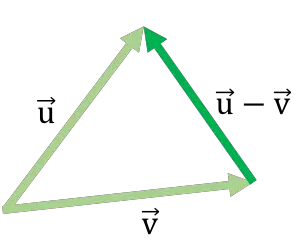
Diese Methode zum Subtrahieren von Vektoren ähnelt der Kopf- und Schwanzmethode zum Addieren von Vektoren .

Polygonmethode

Nachdem wir gesehen haben, wie man die Subtraktion zweier Vektoren grafisch löst, werden wir sehen, wie das geht, wenn wir mehr als zwei Vektoren haben.

Wenn Sie drei oder mehr Vektoren subtrahieren möchten, gibt es eine Technik, mit der Sie die Berechnung beschleunigen und alle Vektoren auf einmal subtrahieren können. Diese Technik wird Polygonmethode genannt und besteht aus der sukzessiven Anwendung der Kopf-an-Schwanz-Methode der Vektoraddition.

Jetzt denken Sie wahrscheinlich: Vektoren hinzufügen ? Es ist falsch korrigiert… Na ja, nein! eh eh

Es stellt sich heraus, dass das Subtrahieren zweier Vektoren dasselbe ist wie das Addieren eines Vektors plus dem entgegengesetzten (oder negativen) Vektor des subtrahierenden Vektors. Dies liegt an den Additions- und Subtraktionseigenschaften von Vektoren:

Daher müssen wir folgende Schritte ausführen, um 3 oder mehr Vektoren mit der Polygonmethode zu subtrahieren:

1. Zuerst müssen wir den Umkehrvektor jedes Subtraktionsvektors finden. Es ist so einfach wie das Umkehren der Richtung und Ausrichtung aller subtrahierten Vektoren.
2. Dann platzieren wir jeden entgegengesetzten Vektor nacheinander neben dem Vektor, den Sie nicht subtrahieren. Damit der Ursprung eines Vektors mit dem Ende eines anderen Vektors zusammenfällt.
3. Schließlich ist das Ergebnis der Vektorsubtraktion der Vektor, der durch Verbinden des Anfangs des ersten Vektors mit dem Ende des letzten Vektors erhalten wird.

Schauen Sie sich das folgende Beispiel an, in dem eine Subtraktion mit 4 Vektoren durchgeführt wird:

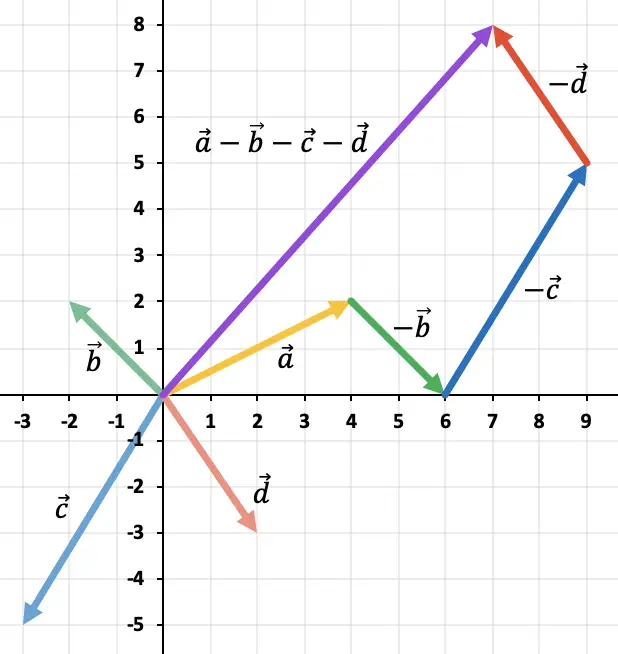
Beachten Sie, dass die beiden Komponenten dieses Vektors das Vorzeichen ändern müssen, um den Gegenvektor eines Vektors zu finden.

Wie berechnet man numerisch die Subtraktion zweier Vektoren?

Sobald wir bereits wissen, wie man Vektoren vom Diagramm subtrahiert, werden wir sehen, wie man eine Vektorsubtraktion numerisch oder algebraisch berechnet.

Zum Beispiel die Subtraktion zwischen Vektoren

Und

Ost:

Probleme mit der Vektorsubtraktion gelöst

Übung 1

Berechnen Sie die Vektorsubtraktion grafisch

weniger

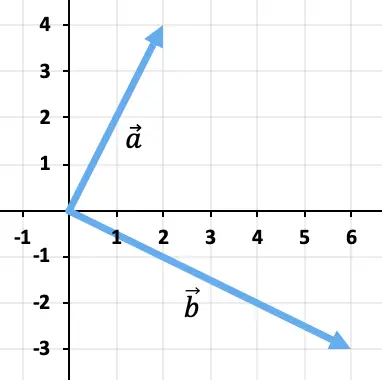
Um die beiden Vektoren zu subtrahieren, verwenden wir die Dreiecksmethode. Die Punkte sind bereits am selben Anwendungspunkt (dem Koordinatenursprung) platziert, sodass das Ergebnis der Subtraktion der Vektor ist, der vom Ende von ausgeht

am Ende von

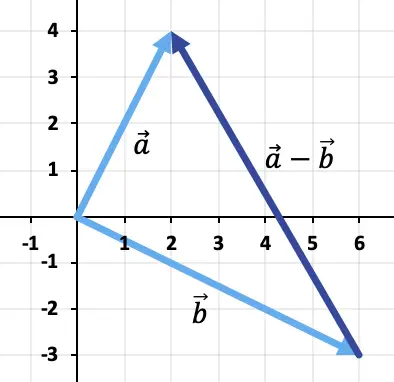
Übung 2

Finden Sie die Subtraktion von Vektoren grafisch

weniger

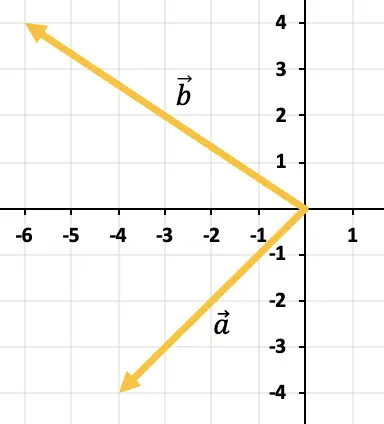
Um die beiden Vektoren zu subtrahieren, verwenden wir die Dreiecksregel. Die Punkte sind bereits am gleichen Anwendungspunkt platziert (am Anfang der X-Achse und der Y-Achse), sodass das Ergebnis der Subtraktion der Vektor ist, der vom Ende von ausgeht

am Ende von

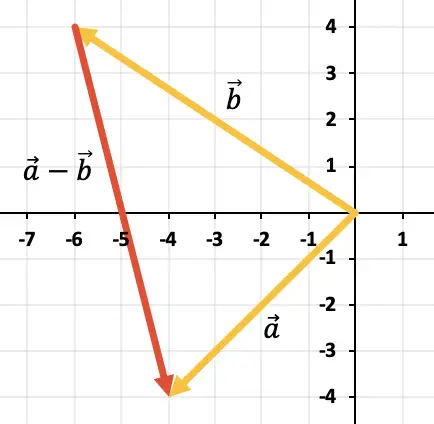
Übung 3

Lösen Sie die folgende Vektoroperation grafisch:

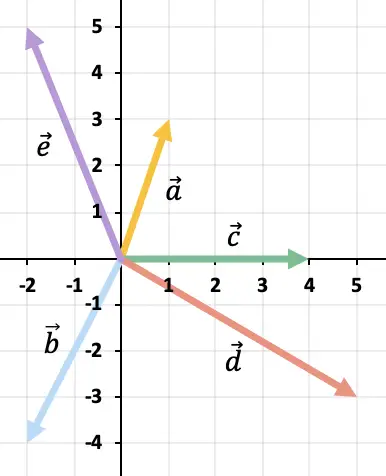
Da es mehr als zwei Vektoren gibt, verwenden wir die Polygonregel, um die Vektorsubtraktion zu lösen. Dazu müssen wir nacheinander die Gegenvektoren der übrigen Vektoren darstellen. Und das Ergebnis ist der Vektor, der am Ursprung des Vektors beginnt

dorthin, wo der letzte Gegenvektor endet.

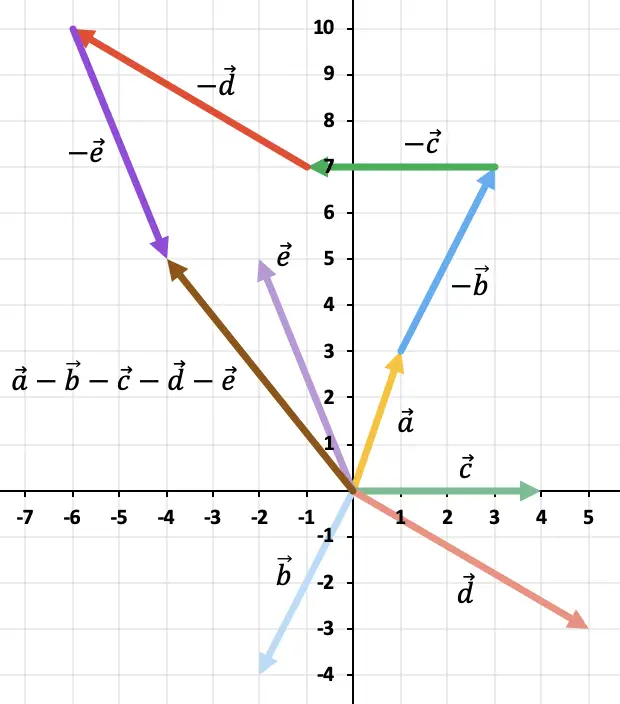
Übung 4

Bestimmen Sie numerisch das Ergebnis der Subtraktion der folgenden Vektoren:

Um zwei Vektoren numerisch zu subtrahieren, müssen Sie ihre jeweiligen Koordinaten subtrahieren:

Übung 5

Lösen Sie analytisch die folgende Vektoroperation:

Um Vektoren numerisch (oder analytisch) zu subtrahieren, müssen wir ihre jeweiligen Komponenten subtrahieren: