In diesem Artikel erklären wir, was Unbestimmtheit ist. Sie erfahren, was alle Arten von Unbestimmtheiten sind und wie Sie sie lösen können. Darüber hinaus können Sie Schritt für Schritt gelöste Übungen zu den Funktionsgrenzen aller Unbestimmtheiten sehen.
Was sind Unbestimmtheiten?
Unbestimmtheiten, auch unbestimmte Formen genannt, sind mathematische Ausdrücke, die bei der Berechnung der Grenzen von Funktionen auftreten, deren Ergebnis nicht definiert ist. Um die Unbestimmtheiten der Grenzen aufzulösen, ist es daher notwendig, ein Vorverfahren anzuwenden, das von der Art der Funktion abhängt.
Das heißt, wenn wir Unbestimmtheit erreichen, bedeutet das nicht, dass der Grenzwert nicht existiert oder dass er nicht gelöst werden kann, sondern dass wir Änderungen an der Funktion vornehmen müssen, um die Lösung des Grenzwerts zu finden.
Arten von Unbestimmtheiten
Unbestimmte oder unbestimmte Formen werden in die folgenden Typen eingeteilt:
- Unbestimmtheit Unendlich minus Unendlich (∞-∞)
- Anzahl der Unbestimmtheit zwischen Null (k/∞)
- Nullunbestimmtheit zwischen Null (0/0)
- Unendliche Unbestimmtheit zwischen Unendlichkeit (∞/∞)
- Unbestimmtheit 1 ins Unendliche erhoben (1 ∞ )
- Nullunbestimmtheit auf Null erhöht (0 0 )
- Null-Unbestimmtheit für Unendlich (0·∞)
- Nullunbestimmtheit ins Unendliche erhöht (0 ∞ )
- Unendliche Unbestimmtheit auf Null gebracht (∞ 0 )
Wir werden dann sehen, wie wir alle Arten von Unbestimmtheiten auflösen können.
Unendliche minus unendliche Unbestimmtheit
Die unbestimmte Form Unendlich minus Unendlich ist nicht gleich Null, da wir zwei sehr große Zahlen subtrahieren, aber nicht wissen, welche größer ist. Das Ergebnis der Differenz der Unendlichkeiten hängt daher von der Ordnung jeder Unendlichkeit ab.
Die Auflösung dieser Art von Unbestimmtheit ist nicht einfach, da je nach Art der Funktion das eine oder andere Verfahren angewendet werden muss. Daher empfehlen wir Ihnen, die vollständige Erklärung unter folgendem Link anzusehen:
➤ Siehe: So lösen Sie die Unbestimmtheit Unendlich minus Unendlich
Anzahl der Unbestimmtheit zwischen Null
Die Unbestimmtheit einer durch Null dividierten Konstante erhält man, wenn der Nenner einer rationalen Funktion gestrichen wird.
Das Ergebnis dieser Art unbestimmter Form wird immer unendlicher oder weniger unendlich sein, andernfalls existiert der Grenzwert der Funktion nicht. Sehen wir uns an, wie diese Unbestimmtheit berechnet wird, indem wir als Beispiel einen Grenzwert lösen:
Wir haben die Unbestimmtheit einer Zahl dividiert durch Null erhalten, also müssen wir die seitlichen Grenzen der Funktion berechnen:
➤ Siehe: Was sind seitliche Begrenzungen?
Die beiden seitlichen Grenzen der Funktion führen zum gleichen Ergebnis. Per Definition ergibt der Grenzwert der Funktion, wenn x gegen 0 geht, minus Unendlich:
Beachten Sie, dass der Grenzwert der Funktion an diesem Punkt nicht existieren würde, wenn die seitlichen Grenzen unterschiedliche Werte ergeben hätten.
Null zwischen Null Unbestimmtheit
Der unbestimmte Grenzwert Null dividiert durch Null kommt sehr häufig vor und wird bei Funktionen mit Brüchen erhalten, bei denen sich Zähler und Nenner aufheben.
Diese Art unbestimmter Grenze wird je nach Funktion unterschiedlich aufgelöst. Wenn die Funktion beispielsweise Wurzeln hat, müssen verschiedene Schritte ausgeführt werden. Die verschiedenen Auflösungen dieser Art von Unbestimmtheit können Sie im folgenden Link sehen:
➤ Siehe: So lösen Sie die Nullunbestimmtheit zwischen Null
Unendliche Unbestimmtheit zwischen dem Unendlichen
Unendliche Unbestimmtheit zwischen Unendlichkeit tritt normalerweise in den unendlichen Grenzen von Funktionen mit Brüchen auf. Obwohl Unbestimmtheit der Quotient zweier Unendlichkeiten ist, muss das Ergebnis nicht unbedingt Unendlichkeit sein.
Diese Art unbestimmter Form wird durch Vergleich aufgelöst. Das heißt, der Grad des Zählers und der Grad des Nenners werden beobachtet und je nachdem, welcher Wert größer ist, ist das Grenzergebnis das eine oder das andere. Alle Fälle können Sie unter folgendem Link einsehen:
➤ Siehe: gelöste Übungen zu unendlichen Grenzen zwischen Unendlich
Unbestimmtheit 1 ins Unendliche erhöht
Mathematisch könnte man denken, dass 1 bis Unendlich 1 ergibt, da jede Potenz von 1 gleich 1 ist. Dieser Term ist jedoch eine Unbestimmtheit und daher kann man sein Ergebnis nicht so einfach ableiten.
Diese Art von Unbestimmtheit wird durch Anwendung der folgenden Formel berechnet:
![\displaystyle\lim_{x\to+\infty}f(x)^{g(x)}=\lim_{x\to+\infty}e^{g(x)\cdot [f(x)-1]}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e6bc13731241df168c3dc37d3e3b8e58_l3.png "Rendered by QuickLaTeX.com")
Beispielsweise ist der folgende Grenzwert unbestimmt, da er die Potenz der Unendlichkeit angibt:
Wir müssen daher die Formel für diese Art von Unbestimmtheit verwenden:
![\displaystyle\lim_{x\to+\infty}e^{x\cdot\left[1-\frac{1}{x}-1\right]}=\lim_{x\to+\infty}e^{x\cdot\left[-\frac{1}{x}\right]}=\lim_{x\to+\infty}e^{-1}=\frac{1}{e}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e577daa5f0e768ca16bfe27a4d7a8a85_l3.png "Rendered by QuickLaTeX.com")
Damit haben wir die ins Unendliche angehobene unbestimmte Grenze bereits gelöst.
Null Unbestimmtheit auf Null gebracht
Nullunbestimmtheit zur Nullpotenz tritt innerhalb der Grenzen komplizierter Funktionen auf.
Um diese Art von unbestimmtem Grenzwert aufzulösen, müssen Sie die folgende Grenzwerteigenschaft verwenden:
Der folgende Grenzwert ergibt beispielsweise die unbestimmte Form 0 hoch 0:
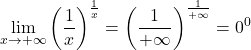
Wenn wir jedoch Logarithmen auf den Grenzwert anwenden, können wir seinen Wert ermitteln:
![\begin{array}{l}\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln\left(\frac{1}{x}\right)}}=\\[5ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln\left(\frac{1}{x}\right)}{x}}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln1-\ln x}{x}}}=\\[5ex]=\displaystyle e^{^{\displaystyle\lim_{x\to +\infty}\frac{-\ln x}{x}}}=e^{^{\displaystyle\frac{-\infty}{+\infty}}}=e^0=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04165b15f4b40bbe84ae5a4b214d4846_l3.png "Rendered by QuickLaTeX.com")
Null Unbestimmtheit für die Unendlichkeit
Es ist schwierig, der Unbestimmtheit des Produkts aus Null und Unendlich zu begegnen, aber das bedeutet nicht, dass es leicht zu bestimmen ist.
Es gibt keine einheitliche Methode zur Lösung dieser Art von Unbestimmtheit, sie hängt jedoch von der Art der Funktion ab. In diesem Fall müssen wir die Funktion in eine unendliche Unbestimmtheit geteilt durch Unendlich oder eine Null-Unbestimmtheit geteilt durch Null umwandeln und von dort aus die Lösungsmethoden anwenden, die wir oben für jede Unbestimmtheit gesehen haben.
Wenn also der Grenzwert einer Funktion 0 und der Grenzwert der anderen Funktion ∞ ist:
Wir können diesen Typ auf unbestimmte Zeit transformieren, indem wir die folgenden Änderungen vornehmen:
![\displaystyle\lim_{x\to a}f(x)\cdot g(x)\begin{cases}\displaystyle\lim_{x\to a}\frac{f(x)}{\displaystyle\frac{1}{g(x)}}=\frac{0}{0}\\[10ex]\displaystyle\lim_{x\to a}\frac{g(x)}{\displaystyle\frac{1}{f(x)}}=\frac{\infty}{\infty}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-df402461269ae26c30768fc0bf83f2ea_l3.png "Rendered by QuickLaTeX.com")
Sehen wir uns an, wie das geht, indem wir als Beispiel einen unbestimmten Grenzwert lösen:
Wir bearbeiten die Funktion, um eine unendliche Unbestimmtheit über die Unendlichkeit zu erhalten, und finden dann den Grenzwert:
![\begin{array}{l}\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=\lim_{x\to +\infty}\frac{x}{\displaystyle\frac{1}{e^{-x}}}=\\[6ex]=\displaystyle \lim_{x\to +\infty}\frac{x}{e^x}=\frac{+\infty}{e^{+\infty}}=\frac{+\infty}{+\infty}=0\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c29bbb439514449cd12fd8d66e327af_l3.png "Rendered by QuickLaTeX.com")
Null-Unbestimmtheit ins Unendliche erhöht
Die ins Unendliche erhöhte Unbestimmtheitsnull ist etwas schwer zu verstehen, da wir eine sehr kleine Zahl auf eine sehr große Zahl erhöhen.
Wenn diese unbestimmten Formen erhalten werden, muss die folgende Formel verwendet werden:
Lassen Sie uns ein Beispiel lösen, um besser zu verstehen, wie diese Art von Unbestimmtheit berechnet wird:
![\begin{array}{l}\displaystyle\lim_{x\to 0^+}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to 0^+}\frac{1}{x}\cdot \ln(x)}}=\\[3.5ex]\displaystyle =e^{^{\displaystyle\frac{1}{0^+}\cdot \ln(0^+)}}=e^{+\infty\cdot (-\infty)}\\[3ex]\displaystyle =e^{-\infty}=\frac{1}{e^{+\infty}}=0\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ca354428ea8889a956a9b77b04a088f_l3.png "Rendered by QuickLaTeX.com")
Unendliche Unbestimmtheit auf Null gebracht
Normalerweise ergibt jede Potenz, die auf Null erhöht wird, 1, die Unbestimmtheit der Unendlichkeit, die auf Null erhöht wird , muss jedoch nicht unbedingt so sein.
Wie bei den Unbestimmtheiten Null auf Null erhöht und Null auf Unendlich erhöht, ist es zur Auflösung dieser Art unbestimmter Grenze notwendig, Logarithmen anzuwenden:
Sehen wir uns an, wie diese Art unbestimmter Grenzen gelöst wird, indem wir Schritt für Schritt ein Beispiel berechnen:
![\begin{array}{l}\displaystyle\lim_{x\to +\infty}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln(x)}}=\\[3ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln(x)}{x}}}=e^{^{\displaystyle\frac{\ln(+\infty)}{+\infty}}}=\\[3ex]\displaystyle =e^{^{\displaystyle\frac{+\infty}{+\infty}}}=e^0=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a45090015a206189aca3884f8b2cab30_l3.png "Rendered by QuickLaTeX.com")