Unbestimmtheit unendlich minus unendlich (∞-∞)

In diesem Artikel erklären wir, wie man die unendliche minus unendliche (∞-∞) Unbestimmtheit löst. Sie finden Beispiele für diese Unbestimmtheit bei verschiedenen Arten von Funktionen und können darüber hinaus mit Übungen üben, die Schritt für Schritt zur Unbestimmtheit unendlich minus unendlich gelöst werden.

Lösung der Unbestimmtheit unendlich minus unendlich

Wenn der Grenzwert einer Funktion Unendlich minus Unendlich ergibt, bedeutet dies, dass es sich um eine Unbestimmtheit (oder eine unbestimmte Form) handelt. Das heißt , der Grenzwert einer Funktion, die Unbestimmtheit minus Unendlich ergibt, kann nicht durch direkte Berechnung bestimmt werden, sondern es muss ein vorläufiges Verfahren durchgeführt werden.

Um die unendliche minus unendliche Unbestimmtheit zu lösen, müssen wir daher zunächst ein Verfahren anwenden, das von der Art der Funktion abhängt: Wenn es sich um eine Polynomfunktion handelt, kann sie durch Vergleich berechnet werden. Wenn es sich um eine rationale Funktion handelt, müssen Brüche reduziert werden einen gemeinsamen Nenner, und wenn es sich um eine irrationale Funktion handelt, muss sie mit dem Konjugat multipliziert werden.

\displaystyle\lim_{x\to+\infty}\Bigl(f(x)-g(x)\Bigr)=\infty-\infty

Als nächstes werden wir anhand von Beispielen sehen, wie die Unbestimmtheit unendlich minus unendlich in jedem Funktionstyp aufgelöst wird.

Unendliche minus unendliche Unbestimmtheit in Polynomfunktionen

In einem Polynom ist die Unbestimmtheit Unendlich minus Unendlich gleich der Unendlichkeit höchster Ordnung, das heißt, der Term höchster Ordnung bestimmt das positive oder negative Vorzeichen der Unendlichkeit.

Schauen Sie sich zum Beispiel den Grenzwert der folgenden Polynomfunktion an, die die unbestimmte Form Unendlich minus Unendlich ergibt:

\displaystyle\lim_{x\to+\infty}\bigl(x^2-3x\bigr)=(+\infty)^2-3\cdot (\infty)=+\infty-\infty=+\infty

In diesem Fall ist der Term x 2 vom zweiten Grad und der Term 3x vom ersten Grad, sodass das Monom x 2 dominant ist, da es von höherer Ordnung ist. Daher ist das Ergebnis des Grenzwerts die aus diesem Term erhaltene Unendlichkeit.

Schauen Sie sich diese anderen Beispiele an:

\begin{array}{l}\displaystyle\lim_{x\to+\infty}\bigl(x^5-4x^2-3x\bigr)=(+\infty)^5=+\infty\\[5ex]\displaystyle\lim_{x\to-\infty}\bigl(-3x^2-5x\bigr)=-3\cdot (-\infty)^2=-3\cdot \infty=-\infty\\[5ex]\displaystyle\lim_{x\to+\infty}\bigl(x^7-5x^4+x^3-2x-10\bigr)=(+\infty)^7=+\infty\end{array}

Kurz gesagt, wenn wir in Polynomfunktionen Grenzen für die Unendlichkeit festlegen , müssen wir einfach die Unendlichkeit in den Term höchsten Grades einsetzen und alle anderen Terme ignorieren.

Unbestimmtheit unendlich minus unendlich mit Brüchen

Wenn die Unbestimmtheit Unendlich minus Unendlich bei einer Addition oder Subtraktion algebraischer Brüche auftritt , müssen wir zuerst die Addition oder Subtraktion der Brüche durchführen und dann den Grenzwert berechnen.

Sehen wir uns an, wie man die Unbestimmtheit Unendlich minus Unendlich in einer Funktion mit Brüchen berechnet, indem man ein Beispiel Schritt für Schritt löst:

\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)

Versuchen wir zunächst, den Grenzwert zu berechnen:

\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}

Aber wir erhalten die Unbestimmtheit ∞-∞.

Zuerst müssen wir also die Brüche subtrahieren. Dazu reduzieren wir Brüche auf einen gemeinsamen Nenner, das heißt, wir multiplizieren Zähler und Nenner des einen Bruchs mit dem Nenner des anderen:

\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}

Und da nun beide Brüche den gleichen Nenner haben, können wir sie zu einem einzigen Bruch kombinieren:

\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}

Wir arbeiten im Zähler und Nenner:

\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}

Und zum Schluss berechnen wir noch einmal den Grenzwert:

\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}

In diesem Fall ergibt die unendliche Unbestimmtheit zwischen Unendlichkeit +∞, weil der Grad des Zählers größer ist als der Grad des Nenners.

➤ Siehe:Was ist Unendlichkeit zwischen Unendlichkeit?

Unbestimmtheit unendlich minus unendlich mit Wurzeln

Wenn bei der Radikaladdition oder -subtraktion die Unbestimmtheit Unendlich minus Unendlich auftritt , müssen wir die Funktion zunächst mit dem konjugierten Radikalausdruck multiplizieren und dividieren und dann nach dem Grenzwert auflösen.

Wir werden anhand eines Schritt-für-Schritt-Beispiels sehen, wie man die Unbestimmtheit unendlich minus unendlich in einer irrationalen Funktion löst:

\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)

Versuchen wir zunächst, den Limes der Funktion mit Radikalen zu lösen:

\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}

Allerdings erhalten wir die unbestimmte Form ∞-∞. Um also zu wissen, wie viel Unbestimmtheit Unendlichkeit minus Unendlichkeit ist, müssen wir das erläuterte Verfahren anwenden.

Da die Funktion Radikale hat, multiplizieren und dividieren wir die gesamte Funktion durch den konjugierten irrationalen Ausdruck:

\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}

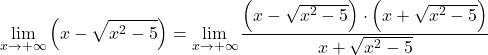
Der algebraische Ausdruck des Zählers entspricht der bemerkenswerten Identität des Produkts einer Summe durch eine Differenz. Wir können den Ausdruck daher vereinfachen:

\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}

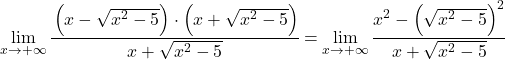
Wir vereinfachen nun die Wurzel des Grenzwerts, da diese quadriert wird:

\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}

Wir operieren mit dem Zähler des Bruchs:

\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}

\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}

Und schließlich wiederholen wir die Berechnung des Grenzwerts:

\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}

Das Ergebnis der Grenze ist daher 0, da jede durch Unendlich geteilte Zahl gleich Null ist.

Unendlich minus unendlich Unbestimmtheitsprobleme gelöst

Übung 1

Lösen Sie den folgenden Grenzwert, wenn x sich plus Unendlich nähert:

\displaystyle\lim_{x\to +\infty}(7x^2-2x^3)

In diesem Grenzfall hat der Term höchster Ordnung den dritten Grad, daher konzentrieren wir uns auf die Unendlichkeit, die sich aus diesem Term ergibt.

\displaystyle\lim_{x\to +\infty}(+7x^2-2x^3)=+\infty^2-\infty^3=+\infty-\infty=\bm{-\infty}

Übung 2

Berechnen Sie den Grenzwert der folgenden Polynomfunktion, wenn x sich der negativen Unendlichkeit nähert:

\displaystyle\lim_{x\to -\infty}(-5x^3-9x^2)

Die kubische negative Unendlichkeit bleibt negativ, aber quadriert wird sie positiv. später Obwohl ihre Vorzeichen durch die Koeffizienten vor ihnen modifiziert werden:

\begin{array}{l}\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\\[3ex]=-5(-\infty)^3-9(-\infty)^2=\\[3ex]=-5\cdot (-\infty)-9\cdot \infty=\\[3ex]=+\infty-\infty\end{array}

Dann wird die unbestimmte Form Unendlichkeit minus Unendlichkeit durch den Term höchster Ordnung (-5x 3 ) definiert, aus dem wir positive Unendlichkeit erhalten:

\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\bm{+\infty}

Übung 3

Bestimmen Sie den Grenzwert der folgenden rationalen Funktion gegen Unendlich:

\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)

Zuerst versuchen wir, den Grenzwert zu berechnen, indem wir die Unendlichkeit in der Funktion ersetzen:

\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}

Aber am Ende haben wir die Unbestimmtheit ∞ – ∞. Deshalb bringen wir die Brüche auf einen gemeinsamen Nenner:

\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}

Und da nun beide Brüche den gleichen Nenner haben, können wir sie zu einem Bruch zusammenfassen:

\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}

Wir machen die Klammern des Zählers:

\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}

Und schließlich bestimmen wir den Grenzwert:

\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}

In diesem Fall ergibt die Unbestimmtheit ∞/∞ +∞, da der Grad des Zählers größer ist als der Grad des Nenners.

Übung 4

Lösen Sie den Grenzwert der folgenden Bruchfunktion, wenn x sich 0 nähert:

\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)

Wir versuchen zunächst wie gewohnt den Grenzwert zu berechnen:

\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}

Aber wir erhalten die unbestimmte Form ∞-∞. Daher müssen wir die Brüche der Funktion auf einen gemeinsamen Nenner reduzieren.

In diesem Fall ist x 4 ein Vielfaches von x 2 . Wenn wir also einfach Zähler und Nenner des zweiten Bruchs mit x 2 multiplizieren, erhalten wir, dass beide Brüche denselben Nenner haben:

\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}

Wir können nun die beiden Brüche subtrahieren:

\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}

Wir versuchen das Limit erneut aufzulösen:

\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}

Aber am Ende haben wir die Unbestimmtheit einer durch Null dividierten Konstante. Daher ist es notwendig, die seitlichen Grenzen der Funktion zu berechnen.

\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty

\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty

Zusammenfassend lässt sich sagen, dass die Lösung des Grenzwerts -∞ lautet, da die beiden seitlichen Grenzen der Funktion am Punkt x=0 -∞ ergeben:

\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}

Übung 5

Lösen Sie den Grenzwert der folgenden Funktion mit Wurzeln ins Unendliche:

\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)

Beim Versuch, den Grenzwert zu lösen, erhalten wir die Unbestimmtheit unendlich minus unendlich:

\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}

Da die Funktion Radikale enthält, müssen wir sie daher mit dem konjugierten Radikalausdruck multiplizieren und dividieren:

\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}

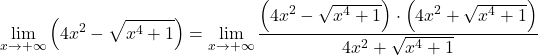
Im Zähler haben wir das bemerkenswerte Produkt einer Summe mit einer Differenz, die gleich der Differenz der Quadrate ist. Noch:

\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}

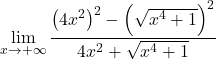
Wir vereinfachen das Radikal zum Quadrat:

\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}

Wir operieren im Zähler:

\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}

\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}

Und schließlich finden wir die Grenze:

\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}

In diesem Fall ist die unendliche Unbestimmtheit geteilt durch Unendlich unendlicher, weil der Grad des Zählers größer ist als der Grad des Nenners (denken Sie daran, dass die Quadratwurzel den Grad um zwei reduziert:

\sqrt{x^4} = x^{4/2} = x^2

).

Übung 6

Lösen Sie den Grenzwert, wenn x sich der Unendlichkeit der folgenden irrationalen Funktion nähert:

\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)

Zunächst versuchen wir wie gewohnt den Grenzwert zu berechnen:

\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}

Aber es gibt uns als Ergebnis die Unbestimmtheit der Differenz der Unendlichkeiten. Da die Funktion Wurzeln hat, müssen wir daher den Ausdruck mit dem konjugierten Radikal multiplizieren und dividieren:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}

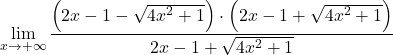
Wir gruppieren die bemerkenswerte Gleichheit des Zählers des Bruchs:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}

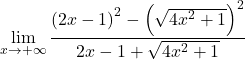
Wir lösen die Quadratwurzel:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}

Wir lösen die bemerkenswerte Identität des Quadrats einer Differenz:

\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}

Wir operieren im Zähler:

\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}

\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}

Und schließlich berechnen wir den Wert des Grenzwerts im Unendlichen:

\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =

Auch wenn im Nenner ein x zum Quadrat steht, ist sein Grad tatsächlich 1, da er innerhalb einer Wurzel liegt:

\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .

Daher ist das Ergebnis der Unbestimmtheit -∞/+∞ die Division der Koeffizienten von x höheren Grades, da der Grad des Zählers derselbe ist wie der Grad des Nenners.

\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}

Beachten Sie, dass der Nenner zwei Terme ersten Grades enthält

\bigl(2x

Und

\sqrt{4x^2}\bigr)

, um die Unbestimmtheit -∞/+∞ aufzulösen, ist es notwendig, alle Koeffizienten der Terme ersten Grades zu nehmen, also die

2

von

2x

und das

\sqrt{4}

von

\sqrt{4x^2}.

Übung 7

Berechnen Sie den Grenzwert, wenn x sich 1 der folgenden Funktion mit Brüchen nähert:

\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)

Wenn wir versuchen, den Grenzwert zu ermitteln, erhalten wir den unbestimmten Grenzwert von Unendlich minus Unendlich:

\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}

Wir müssen also die Brüche auf einen gemeinsamen Nenner bringen, oder mit anderen Worten, wir müssen den Zähler und den Nenner des einen Bruchs mit dem Nenner des anderen multiplizieren:

\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}

Und da die beiden Brüche nun den gleichen Nenner haben, können wir sie zusammensetzen:

\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}

Wir betreiben:

\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}

\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}

Und wir versuchen das Limit noch einmal zu lösen:

\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}

Aber wir finden die Unbestimmtheit Null dividiert durch Null. Wir müssen daher die Zähler- und Nennerpolynome faktorisieren:

\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}

Jetzt vereinfachen wir den Bruch, indem wir den Faktor entfernen, der sich im Zähler und Nenner wiederholt:

\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}

Und schließlich lösen wir das Limit auf:

\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}

Kommentar verfassen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

Nach oben scrollen