Alle linear unabhängigen und abhängigen Vektoren

Auf dieser Seite erklären wir, was linear unabhängige und linear abhängige Vektoren sind. Außerdem sehen Sie Beispiele dafür, wie Sie feststellen können, ob eine Menge von Vektoren linear abhängig oder unabhängig ist. Darüber hinaus finden Sie Schritt für Schritt Übungen und gelöste Probleme zum Thema lineare Unabhängigkeit und Abhängigkeit.

Was sind linear unabhängige Vektoren?

Eine Menge freier Vektoren ist linear unabhängig , wenn keiner von ihnen als Linearkombination der anderen geschrieben werden kann.

Mit anderen Worten, es ist eine Menge von Vektoren gegeben

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

Diese sind linear unabhängig, wenn die einzige Lösung der folgenden Gleichung ist:

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

Das sind alles Koeffizienten

$a_i$

gleich 0:

$a_1=a_2=\dots = a_n=0$

Geometrisch gesehen sind zwei Vektoren linear unabhängig, wenn sie nicht die gleiche Richtung haben, also nicht parallel sind.

Der Kürze halber sagen wir manchmal direkt, dass es sich um LI-Vektoren handelt. Oder dass die Vektoren lineare Unabhängigkeit haben.

Was sind linear abhängige Vektoren?

Offensichtlich bedeuten linear abhängige Vektoren das Gegenteil von linear unabhängigen Vektoren. Seine Definition lautet daher:

Eine Menge freier Vektoren der Ebene ist linear abhängig , wenn einer von ihnen als lineare Kombination anderer Vektoren ausgedrückt werden kann, die das System bilden.

Mit anderen Worten, es ist eine Menge von Vektoren gegeben

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

Diese sind linear abhängig, wenn es eine Lösung für die folgende Gleichung gibt:

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

in dem es einen bestimmten Koeffizienten gibt

$a_i$

ist von 0 verschieden:

$a_i\neq 0$

Auch das Umgekehrte gilt: Wenn ein Vektor eine Linearkombination anderer Vektoren ist, dann sind alle Vektoren in der Menge linear abhängig.

Wenn außerdem zwei Vektoren parallel sind, bedeutet dies, dass sie linear abhängig sind.

Manchmal werden sie auch abgekürzt und einfach LD-Vektoren genannt. Oder sogar, dass die Vektoren eine lineare Abhängigkeit haben.

Beispiel dafür, wie man erkennt, ob Vektoren linear abhängig oder unabhängig sind

Wir werden dann ein typisches Beispiel für linear abhängige und unabhängige Vektoren sehen.

Bestimmen Sie, ob die folgenden drei dreidimensionalen Vektoren eine lineare Abhängigkeit oder Unabhängigkeit haben:

$\vv{\text{u}} = (1,5,2)$

$\vv{\text{v}} = (-2,3,-1)$

$\vv{\text{w}} = (4,2,1)$

Zuerst müssen wir die Linearkombinationsbedingung angeben:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

Jetzt ersetzen wir jeden Vektor durch seine Koordinaten. Wie Null, was dem Nullvektor entspricht:

$a_1(1,5,2)+a_2(-2,3,-1)+ a_3(4,2,1)=(0,0,0)$

Koeffizienten multiplizieren Vektoren, daher ist der folgende Ausdruck äquivalent:

$(a_1,5a_1,2a_1)+(-2a_2,3a_2,-a_2) + (4a_3,2a_3,a_3)=(0,0,0)$

Wir fügen Vektoren hinzu:

$(a_1-2a_2+4a_3 \ , \ 5a_1+3a_2+2a_3 \ , \ 2a_1-a_2+a_3)=(0,0,0)$

Wenn wir genau hinsehen, entspricht der vorherige Ausdruck drei Gleichungen, da jede Koordinate des linken Vektors gleich jeder Koordinate des rechten Vektors sein muss. Wir haben also ein homogenes System aus 3 Gleichungen mit 3 Unbekannten:

$\left. \begin{array}{l} a_1-2a_2+4a_3 = 0 \\[2ex] 5a_1+3a_2+2a_3 =0\\[2ex] 2a_1-a_2+a_3 = 0 \end{array} \right\}$

Das Einzige, was wir also tun müssen, ist, das Gleichungssystem zu lösen, dessen Unbekannte sind

$a_1, a_2$

Und

$a_3.$

Dazu können Sie jede Methode (Substitutionsmethode, Gaus-Methode, Cramer-Regel usw.) verwenden. Um jedoch zu wissen, ob die Vektoren LI oder LD sind, reicht es zu bestimmen, ob es eine andere Lösung als die triviale Lösung gibt (alle Koeffizienten gleich Null). ALSO:

Wenn die Determinante der aus den Komponenten der Vektoren zusammengesetzten Matrix von Null verschieden ist, bedeutet dies, dass das Gleichungssystem nur eine Lösung hat (
$a_1=a_2=a_3=\dots=0$

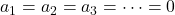
) und daher sind die Vektoren linear unabhängig
Wenn andererseits die Determinante der aus den Komponenten der Vektoren zusammengesetzten Matrix gleich Null ist, bedeutet dies, dass das Gleichungssystem mehr als eine Lösung hat und die Vektoren daher linear abhängig sind.

Es muss also lediglich die Determinante mit den Koordinaten der Vektoren berechnet werden (da es sich um eine 3×3-Determinante handelt, kann sie mit der Sarrus-Regel gelöst werden). Diese Determinante entspricht den Koeffizienten des vorherigen Gleichungssystems:

$\displaystyle \begin{vmatrix} 1&-2&4\\[1.1ex] 5&3&2 \\[1.1ex] 2&-1&1 \end{vmatrix} = -37 \bm{\neq 0}$

In diesem Fall ist die Determinante ungleich 0, sodass die Vektoren linear unabhängig sind.

Daher ist die einzig mögliche Lösung des Gleichungssystems die triviale Lösung mit allen Unbekannten gleich Null:

$a_1=a_2=a_3=0$

Eigenschaften linear abhängiger und unabhängiger Vektoren

Die lineare Abhängigkeit oder Unabhängigkeit von Vektoren weist die folgenden Merkmale auf:

Zwei Proportionalvektoren sind parallel und daher linear abhängig, da sie die gleiche Richtung haben.

Wenn zwei Vektoren nicht die gleiche Richtung haben oder nicht proportional sind, sind sie ebenfalls linear unabhängig.

Drei koplanare Vektoren (die in derselben Ebene liegen) sind linear unabhängig.

Der Nullvektor
$(\vv{\text{v}}=(0,0,0))$

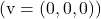
ist linear von jedem Vektor abhängig.

Eine Menge linear unabhängiger Vektoren erzeugt einen Vektorraum und bildet eine Vektorbasis. Stehen die drei Vektoren senkrecht aufeinander, handelt es sich um eine orthogonale Basis. Und wenn ihr Modul ebenfalls gleich 1 ist, entspricht dies einer Orthonormalbasis.

Übungen zur linearen Abhängigkeit und Unabhängigkeit gelöst

Nachfolgend finden Sie einige gelöste Übungen zu linear abhängigen und unabhängigen Vektoren zum Üben.

Übung 1

Bestimmen Sie, ob die folgenden Vektoren linear abhängig oder unabhängig sind:

$\vv{\text{u}} = (1,-2,1)$

$\vv{\text{v}} = (2,1,3)$

$\vv{\text{w}} = (5,-1,1)$

Sehen Sie sich die Lösung an

Wir stellen zunächst die Linearkombinationsbedingung auf:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,-2,1)+a_2(2,1,3)+ a_3(5,-1,1)=(0,0,0)$

$(a_1,-2a_1,a_1)+(2a_2,a_2,3a_2) + (5a_3,-a_3,a_3)=(0,0,0)$

$(a_1+2a_2+5a_3 \ , \ -2a_1+a_2-a_3 \ , \ a_1+3a_2+a_3)=(0,0,0)$

Die vorherige Gleichheit entspricht dem folgenden linearen Gleichungssystem:

$\left. \begin{array}{l} a_1+2a_2+5a_3 = 0 \\[2ex] -2a_1+a_2-a_3 =0\\[2ex] a_1+3a_2+a_3 = 0 \end{array} \right\}$

Nachdem wir das Gleichungssystem angegeben haben, lösen wir die Determinante der Matrix mit ihren Termen:

$\displaystyle \begin{vmatrix} 1&2&5\\[1.1ex] -2&1&-1 \\[1.1ex] 1&3&1 \end{vmatrix} = -29 \bm{\neq 0}$

In diesem Fall ist die Determinante ungleich 0, sodass die drei Vektoren linear unabhängig voneinander sind.

Übung 2

Klassifizieren Sie die folgenden Vektoren als linear abhängig oder unabhängig:

$\vv{\text{u}} = (1,4,3)$

$\vv{\text{v}} = (-2,0,2)$

$\vv{\text{w}} = (3,-1,-4)$

Sehen Sie sich die Lösung an

Zunächst stellen wir die Gleichung der Linearkombination auf:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,4,3)+a_2(-2,0,2)+ a_3(3,-1,-4)=(0,0,0)$

$(a_1,4a_1,3a_1)+(-2a_2,0,2a_2) + (3a_3,-a_3,-4a_3)=(0,0,0)$

$(a_1-2a_2+3a_3 \ , \ 4a_1-a_3 \ , \ 3a_1+2a_2-4a_3)=(0,0,0)$

Aus der vorherigen Gleichheit erhalten wir das folgende homogene Gleichungssystem:

$\left. \begin{array}{l} a_1-2a_2+3a_3= 0 \\[2ex] 4a_1-a_3 =0\\[2ex] 3a_1+2a_2-4a_3 = 0 \end{array} \right\}$

Nachdem wir das Gleichungssystem angegeben haben, lösen wir die Determinante der Matrix mit den Koordinaten der Vektoren auf:

$\displaystyle \begin{vmatrix} 1&-2&3\\[1.1ex] 4&0&-1 \\[1.1ex] 3&2&-4 \end{vmatrix} \bm{= 0}$

In diesem Fall ist die Determinante äquivalent zu 0, die drei Vektoren hängen also linear voneinander ab.

Übung 3

Geben Sie für die folgenden drei Vektoren an, welche Vektorpaare linear abhängig und welche linear unabhängig sind.

$\vv{\text{u}} = (1,2,-2) \qquad \vv{\text{v}} = (2,4,-3) \qquad \vv{\text{w}} = (-4,-8,6)$

Sehen Sie sich die Lösung an

Der einfachste Weg, festzustellen, ob ein Vektorpaar linear abhängig oder unabhängig ist, besteht darin, zu prüfen, ob sie proportional sind.

Wir prüfen zunächst den Vektor

$\vv{\text{u}}$

mit dem Vektor

$\vv{\text{v}} :$

$\cfrac{1}{2} = \cfrac{2}{4} \neq \cfrac{-2}{-3} \ \longrightarrow \ \text{LI}$

Zweitens überprüfen wir den Vektor

$\vv{\text{u}}$

mit dem Vektor

$\vv{\text{w}} :$

$\cfrac{1}{-4} = \cfrac{2}{-8} \neq \cfrac{-2}{6} \ \longrightarrow \ \text{LI}$

Abschließend testen wir den Vektor

$\vv{\text{v}}$

mit dem Vektor

$\vv{\text{w}} :$

$\cfrac{2}{-4} = \cfrac{4}{-8} = \cfrac{-3}{6} = -\cfrac{1}{2} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \text{LD}$

Somit ist das einzige Vektorpaar, das linear voneinander abhängt

$\vv{\text{v}}$

Und

$\vv{\text{w}}.$

Darüber hinaus ist ihre Beziehung wie folgt:

$\vv{\text{v}}= -\cfrac{1}{2} \vv{\text{w}}$

Oder gleichwertig:

$\vv{\text{w}}= -2\vv{\text{v}}$

Die anderen Vektorpaare hingegen sind linear unabhängig.

Übung 4

Untersuchen Sie die lineare Abhängigkeit oder Unabhängigkeit der folgenden 4 Vektoren voneinander:

$\vv{\text{u}} = (0,1,2)$

$\vv{\text{v}} = (-1,-2,0)$

$\vv{\text{w}} = (4,1,-1)$

$\vv{\text{x}} = (-2,-3,2)$

Sehen Sie sich die Lösung an

Wir stellen zunächst die Linearkombinationsbedingung auf:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}+a_4\vv{\text{x}}=0$

$a_1(0,1,2)+a_2(-1,-2,0)+ a_3(4,1,-1)+a_4(-2,-3,2)=(0,0,0)$

$(0,a_1,2a_1)+(-a_2,-2a_2,0) +(4a_3,a_3,-a_3)+(-2a_4,-3a_4,2a_4)=(0,0,0)$

$(-a_2+4a_3-2a_4\ , \ a_1-2a_2+a_3-3a_4 \ , \ 2a_1-a_3+2a_4)=(0,0,0)$

In diesem Fall haben wir ein System aus 3 Gleichungen mit 4 Unbekannten:

$\left. \begin{array}{l} -a_2+4a_3-2a_4 = 0 \\[2ex] a_1-2a_2+a_3-3a_4 =0\\[2ex] 2a_1-a_3+2a_4 = 0 \end{array} \right\}$

Wir können die Determinante der gesamten Systemmatrix nicht lösen, da nur quadratische Matrizen bestimmt werden können. Wir müssen daher alle möglichen Kombinationen von 3×3 Determinanten berechnen und prüfen, ob eine davon gleich 0 ist. In diesem Fall sind die Vektoren linear abhängig. Wenn andererseits alle Determinanten von 0 verschieden sind, sind es die 4 Vektoren linear unabhängig sein.

Wir berechnen die Determinante der Koeffizienten

$a_1, a_2$

Und

$a_3:$

$\displaystyle \begin{vmatrix} 0&-1&4\\[1.1ex] 1&-2&1 \\[1.1ex] 2&0&-1 \end{vmatrix} =13\bm{\neq 0}$

Die Determinante der ersten drei Koeffizienten (oder der ersten drei Vektoren) ist von Null verschieden. Nun versuchen wir es mit der Determinante der Koeffizienten

$a_1, a_2$

Und

$a_4:$

$\displaystyle \begin{vmatrix} 0&-1&-2\\[1.1ex] 1&-2&-3 \\[1.1ex] 2&0&2 \end{vmatrix} \bm{= 0}$

Wir haben eine Nulldeterminante erhalten, daher ist es nicht notwendig, die anderen Determinanten zu berechnen, da wir bereits wissen, dass die 4 Vektoren linear abhängig sind.