Auf dieser Seite wird erklärt, was Umkehrproportionalitätsfunktionen sind und wie man sie grafisch darstellt. Darüber hinaus finden Sie alle Eigenschaften dieser Art von Funktion, die Berechnung ihres Definitionsbereichs sowie mehrere Beispiele und Übungen, die Schritt für Schritt zum Üben gelöst werden.
Was ist eine umgekehrte Proportionalitätsfunktion?
Eine umgekehrte Proportionalitätsfunktion ist eine Funktion, die zwei umgekehrt proportionale Größen in Beziehung setzt, das heißt, dass eine Größe zunimmt, wenn die andere abnimmt, und umgekehrt. Im Allgemeinen werden inverse Proportionalitätsfunktionen durch die folgende Formel definiert:
![]()
Gold
![]()
ist eine Konstante, die Proportionalitätsverhältnis genannt wird.
Umkehrproportionalitätsfunktionen bestehen also immer aus Brüchen mit einem Polynom ersten Grades im Nenner. Sie sind daher eine Art rationale Funktion.
Beispiele für umgekehrte Proportionalitätsfunktionen:
![]()
Allgemein
![]()
ist im Allgemeinen die unabhängige Variable und
![]()
die abhängige Variable, oder mit anderen Worten, die Variable
![]()
darauf ankommen
![]()
Andererseits kann das Proportionalitätsverhältnis (der Zählerterm) positiv oder negativ sein und sein Vorzeichen markiert die Zunahme oder Abnahme der Funktion:
- Wenn die Konstante

negativ ist, nimmt die Funktion zu.
- Stattdessen, wenn die Konstante

positiv ist, nimmt die Funktion ab.
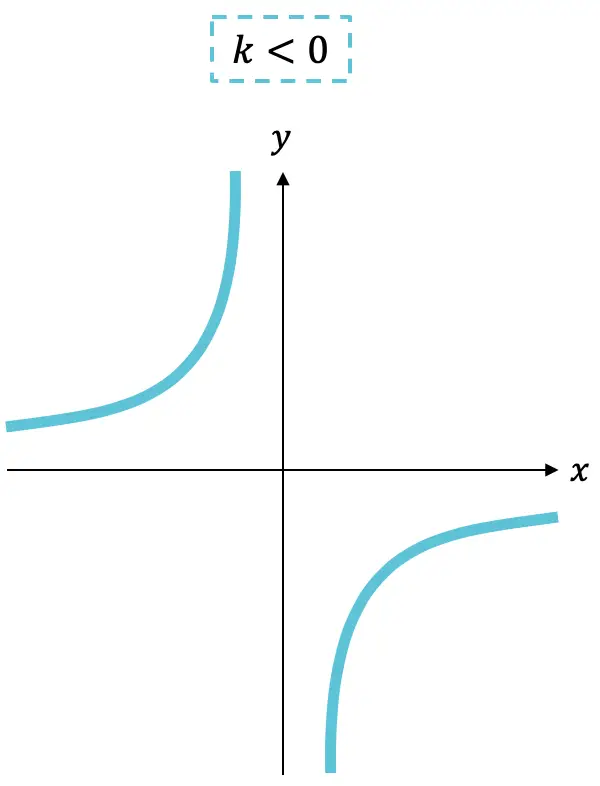
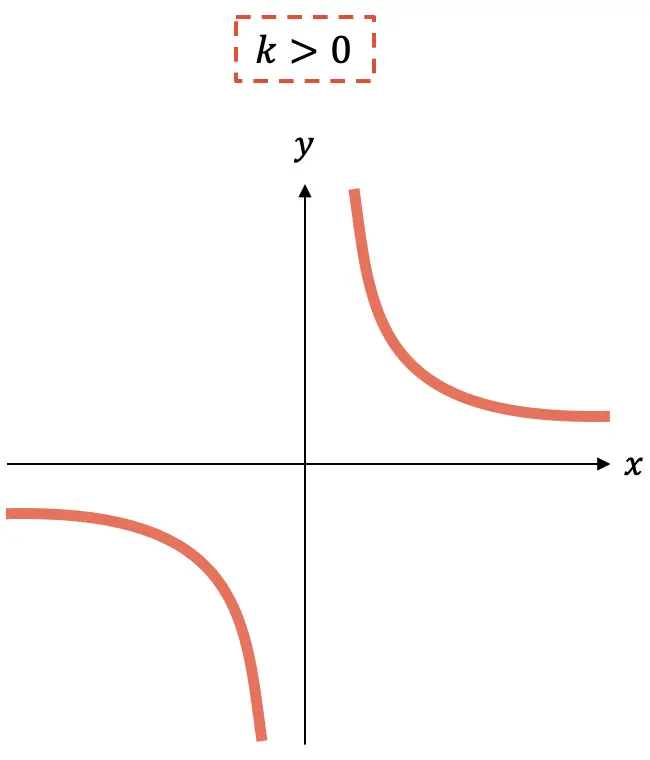
Wie Sie sehen, besteht der Graph einer Umkehrproportionalitätsfunktion immer aus zwei Hyperbeln , die je nach Vorzeichen von k in dem einen oder anderen Quadranten liegen.
Bereich einer umgekehrten Proportionalitätsfunktion
Da es sich um eine Art rationaler Funktion handelt, umfasst der Definitionsbereich einer inversen Proportionalitätsfunktion alle reellen Zahlen mit Ausnahme derjenigen, die aus dem Nenner verschwinden . Denn der Nenner kann niemals Null sein, denn das würde Unendlich ergeben.
Als Beispiel bestimmen wir den Definitionsbereich der folgenden Umkehrproportionalitätsfunktion:
![]()
Um zu wissen, wann der Nenner Null ist, müssen wir seinen Ausdruck auf 0 ausgleichen und die Gleichung lösen:
![]()
![]()
Wenn also x den Wert 1 annimmt, ist der Nenner Null und wir erhalten Unbestimmtheit. Der Definitionsbereich der Funktion ist also das Minus aller reellen Zahlen
![]()
![]()
So zeichnen Sie eine umgekehrte Proportionalitätsfunktion grafisch auf
Wir werden anhand eines Beispiels sehen, wie man eine umgekehrte Proportionalitätsfunktion grafisch darstellt.
- Wir werden die folgende Funktion in einem Diagramm darstellen:
![]()
Als Erstes müssen wir den Definitionsbereich der Funktion ermitteln. Da es sich um einen Bruch handelt, kann der Nenner niemals 0 sein, da dies dann Unendlich ergeben würde. Daher besteht die Domäne ausschließlich aus x, außer wenn der Nenner gestrichen wird.
Wir setzen daher den Nenner gleich 0, um zu sehen, welches x nicht zum Definitionsbereich gehört:
![]()
![]()
Daher umfasst der Definitionsbereich der Funktion alle Zahlen außer 2:
![]()
Sobald wir wissen, welche Zahl nicht zur Domäne gehört, erstellen wir eine Wertetabelle. Um Funktionen umgekehrter Proportionalität darzustellen, müssen 3 oder 4 Punkte links und 3 oder 4 Punkte rechts von der Zahl berechnet werden, die nicht zum Bereich (2) gehört:
![]()

Lassen Sie uns nun die Punkte in einem Diagramm darstellen :
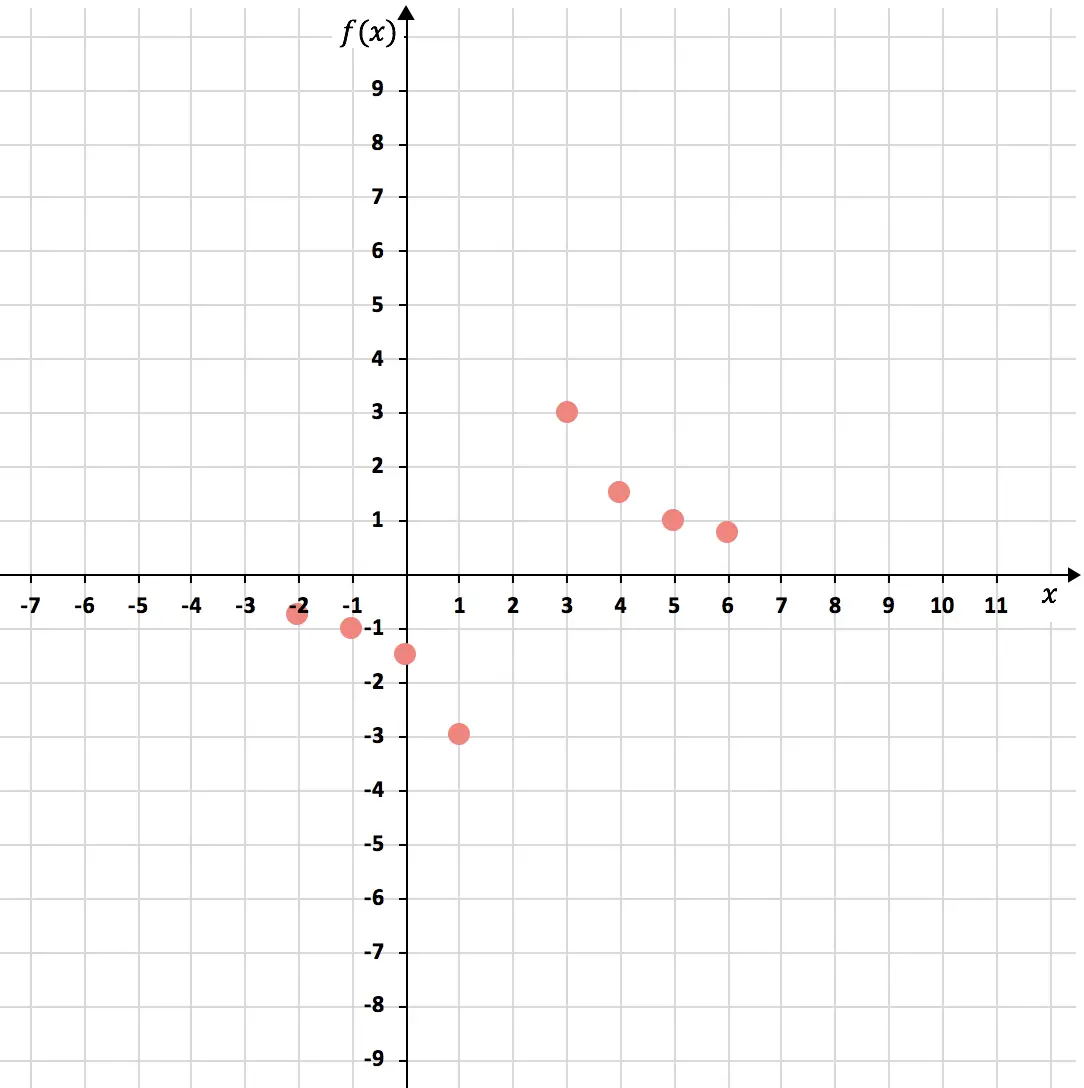
Und schließlich verbinden wir die Punkte und bilden die beiden Hyperbeln der umgekehrten Proportionalitätsfunktion. Zusätzlich verlängern wir die Zweige der Hyperbeln, um anzuzeigen, dass sie weiter wachsen:

Beachten Sie, dass die Funktion approximiert
![]()
, sowohl rechts als auch links. Allerdings kommt er nie ganz an die 2 heran, er kommt ihr sehr nahe, erreicht sie aber nie. ALSO,
![]()
es handelt sich um eine vertikale Asymptote . Es ist, weil
![]()
gehört nicht zum Bereich der Funktion und daher existiert die Funktion zu diesem Zeitpunkt nicht.
Und das Gleiche passiert mit der horizontalen X-Achse. Die Funktion nähert sich an
![]()
aber fass es niemals an. Noch,
![]()
ist eine horizontale Asymptote .
Das bedeutet, dass alle Umkehrproportionalitätsfunktionen unstetig sind, weil sie immer eine Asymptote haben.
Mehr über Asymptoten und Grenzen von Funktionen erfahren Sie auf unserer Website.
Probleme der Umkehrproportionalitätsfunktionen gelöst
Übung 1
Berechnen Sie den Definitionsbereich der folgenden Umkehrproportionalitätsfunktion:
![]()
Eine umgekehrte Proportionalitätsfunktion existiert nicht, wenn der Nenner 0 ist, da die Funktion dann ∞ ergeben würde. Daher müssen wir den Nenner der Funktion auf 0 setzen, um zu sehen, dass x den Nenner aufhebt und daher nicht zum Definitionsbereich gehört.
![]()
![]()
![]()
![]()
Übung 2
Stellen Sie die folgende Umkehrproportionalitätsfunktion grafisch dar:
![]()
Als erstes muss der Definitionsbereich der Funktion berechnet werden:
![]()
![]()
Sobald wir wissen, welche Zahl nicht zur Domäne gehört, erstellen wir ein Wertearray mit der Funktion:

Abschließend stellen wir die erhaltenen Punkte im Diagramm dar und zeichnen die Hyperbeln, wodurch wir die umgekehrte Proportionalitätsfunktion bilden:
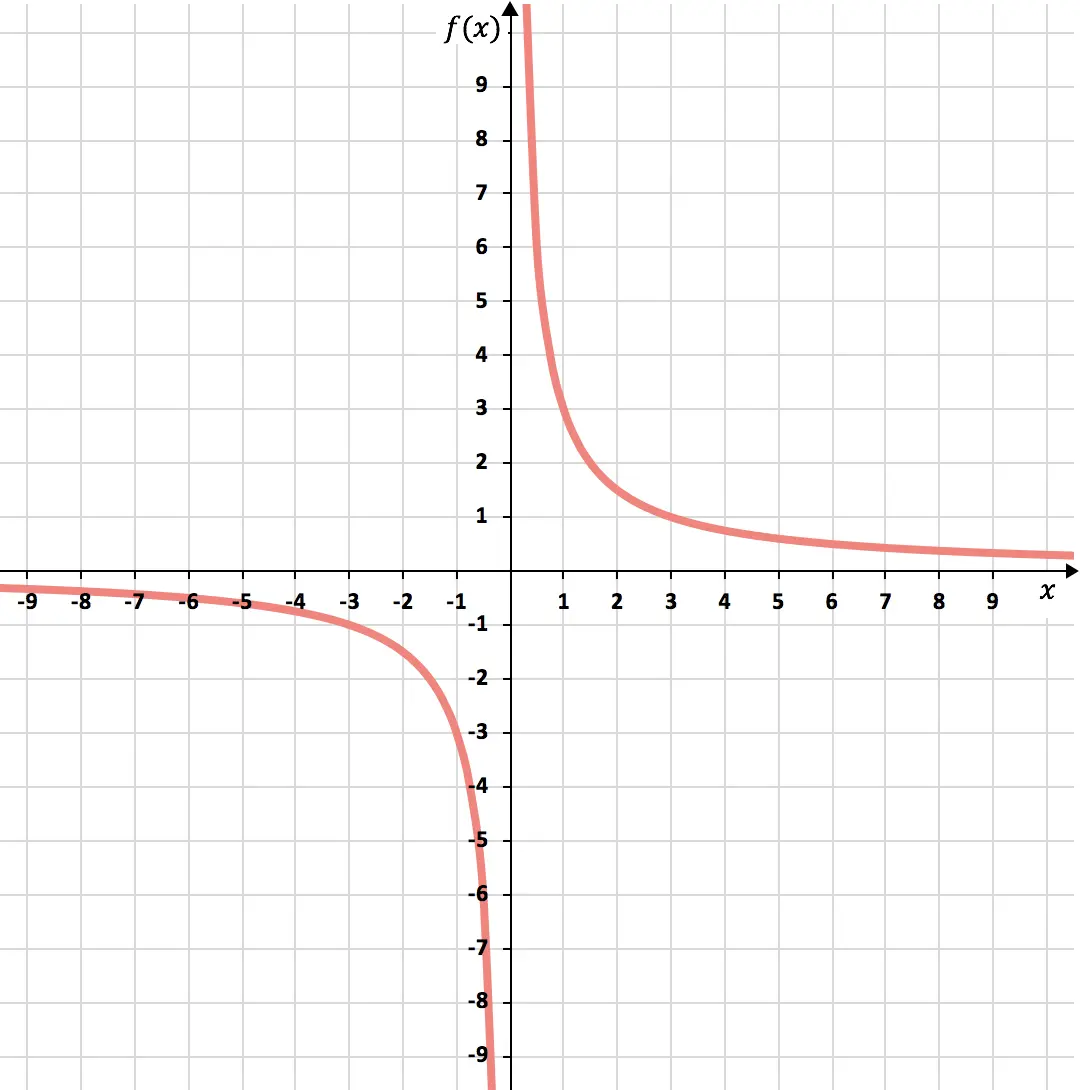
Übung 3
Stellen Sie die folgende Umkehrproportionalitätsfunktion grafisch dar:
![]()
Als erstes muss der Definitionsbereich der Funktion berechnet werden:
![]()
![]()
![]()
Sobald wir den Definitionsbereich der Funktion kennen, erstellen wir eine Wertetabelle:

Abschließend stellen wir die erhaltenen Punkte in einem Diagramm dar und zeichnen die Hyperbeln auf, wodurch wir die umgekehrte Proportionalitätsfunktion bilden:
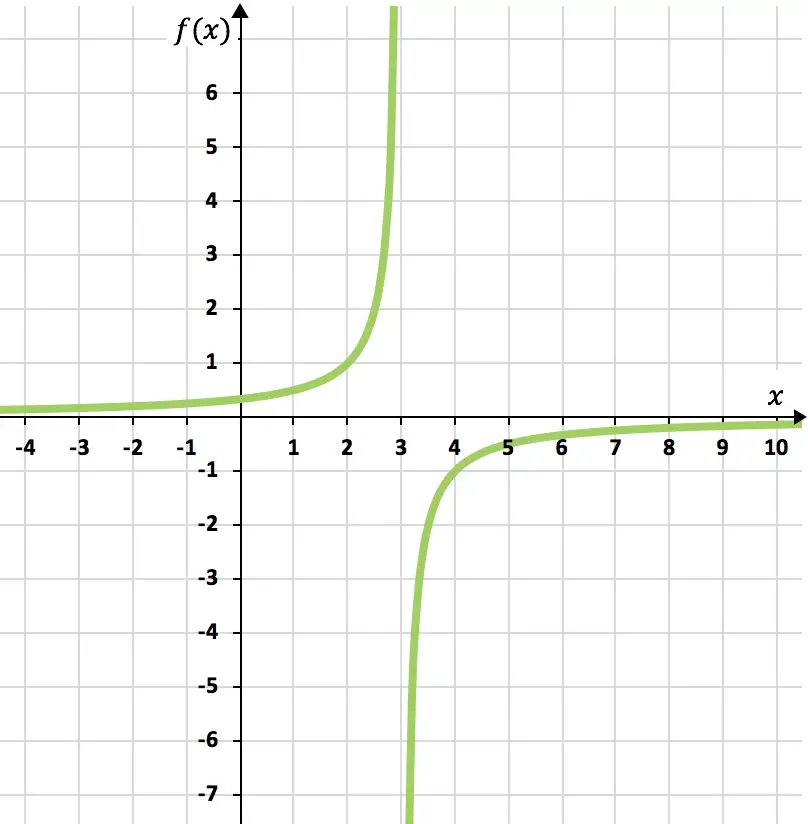
Übung 4
Stellen Sie die folgende Umkehrproportionalitätsfunktion grafisch dar:
![]()
Zuerst müssen wir den Definitionsbereich der Funktion berechnen:
![]()
![]()
![]()
![]()
Sobald wir den Bereich der Funktion kennen, erstellen wir ein Wertearray:
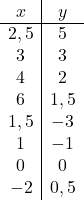
Und schließlich stellen wir die erhaltenen Punkte in einem Diagramm dar und zeichnen die Hyperbeln, wodurch wir die umgekehrte Proportionalitätsfunktion bilden:
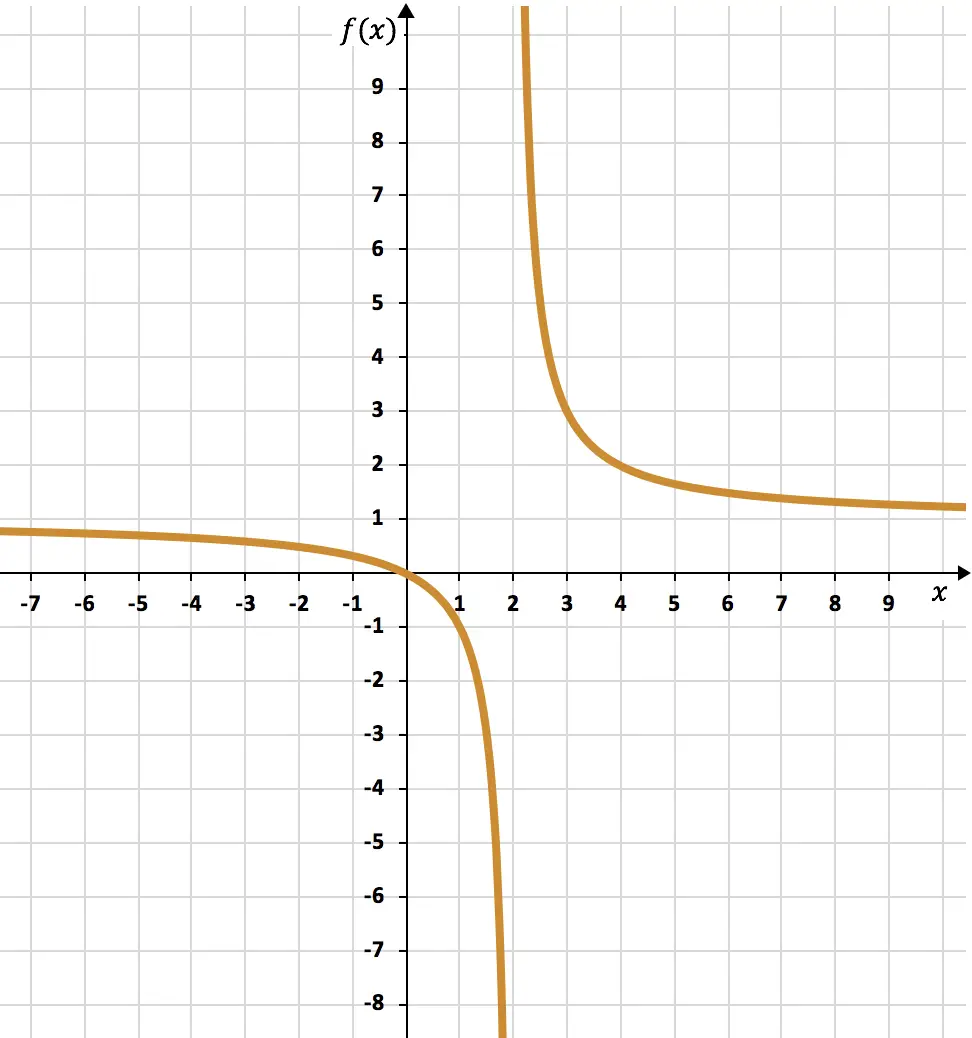
Übung 5
Stellen Sie die folgende rationale Funktion grafisch dar:
![]()
Als erstes muss der Definitionsbereich der Funktion berechnet werden:
![]()
![]()
![]()
![]()
Sobald wir den Definitionsbereich der Funktion kennen, erstellen wir eine Wertetabelle:

Zum Abschluss stellen Sie einfach die erhaltenen Punkte in einem Diagramm dar und zeichnen die Hyperbeln, um so die Bruchfunktion zu bilden:

Anwendungen der Umkehrproportionalitätsfunktion
Die Umkehrproportionalitätsfunktion kommt in vielen Fällen in der Physik und Mathematik vor.
Beispielsweise wird damit der Zusammenhang zwischen Druck und Volumen in einem idealen Gas bei konstanter Temperatur k beschrieben. Diese Funktion wird Boyle-Mariotte-Gesetz (P×V=k) genannt und ist ein Beispiel für eine umgekehrte Proportionalitätsfunktion. Offensichtlich ist der Definitionsbereich dieser Funktion nur auf den positiven Zweig beschränkt, da es keine negativen Volumina oder Drücke gibt.
Der Zusammenhang zwischen Stromstärke und elektrischem Widerstand bei konstanter Potentialdifferenz wird ebenfalls durch eine umgekehrte Proportionalitätsfunktion bestimmt. Diese Funktion ist als Ohmsches Gesetz (V=I×R) bekannt.