▷ So finden Sie die Umkehr- oder Kehrfunktion (gelöste Übungen)

In diesem Artikel erklären wir, was eine Umkehrfunktion (oder Kehrfunktion) ist und wie man die Umkehrfunktion einer Funktion berechnet. Außerdem erfahren Sie, wie Sie leicht erkennen können, ob eine Funktion eine Umkehrung hat oder nicht, und welche Eigenschaften dieser Funktionstyp hat. Abschließend können Sie mit Schritt-für-Schritt-Übungen zu Umkehrfunktionen üben.

Was ist die Umkehrfunktion?

Die Umkehrfunktion, auch Reziprokfunktion genannt, ist die Funktion, deren Bereich der Bereich einer anderen Funktion (der ursprünglichen Funktion) und deren Bereich der Bereich der ursprünglichen Funktion ist. Die Umkehrfunktion der Funktion f wird mit dem Symbol f ^-1 ausgedrückt.

Daher ist die Umkehrfunktion von f(x) die Funktion, die die folgende Bedingung erfüllt:

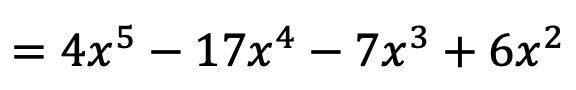
Gold

$f^{-1}$

ist die Umkehrfunktion von

$f.$

Das Konzept einer Umkehrfunktion kann auch durch Funktionskomposition definiert werden, da jede mit ihrer Umkehrfunktion zusammengesetzte Funktion gleich der Identitätsfunktion ist:

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

➤ Siehe: Was ist Funktionskomposition?

Wenn also die vorherige Gleichung erfüllt ist, bedeutet dies Folgendes

$f^{-1}$

ist die Umkehrfunktion (oder Kehrfunktion) von

$f.$

Beispiel einer Umkehrfunktion

Lassen Sie uns angesichts der Definition der Umkehrfunktion ein Beispiel lösen, um ihre Bedeutung besser zu verstehen.

Bestimmen Sie, ob die folgenden Funktionen zueinander invers sind:

$f(x)=2x+1\qquad g(x)=\cfrac{x-1}{2}$

Wenn die beiden Funktionen zueinander invers sind, sind die folgenden zwei Bedingungen erfüllt:

$(f \circ g)(x) = x \qquad \qquad (g \circ f)(x) = x$

Überprüfen wir also, ob beide Gleichungen erfüllt sind. Wir prüfen zunächst

$(f \circ g)(x) = x:$

$\begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}$

➤ Wenn Sie die Berechnung, die wir gerade durchgeführt haben, nicht verstehen, müssen Sie den Link oben für „Wie ist die Zusammensetzung von Funktionen?“ aufrufen. , erklären wir, wie man diese Art von Operation mit Funktionen löst.

So dass

$(f \circ g)(x) = x$

ja, es ist geschafft. ✅

Lassen Sie uns nun die Gleichheit überprüfen

$(g \circ f)(x) = x :$

$\begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}$

Und die Invertibilitätsbedingung

$(g \circ f)(x) = x$

es ist auch gelungen. ✅

Zusammenfassend lässt sich sagen, dass die beiden Funktionen, da beide Gleichungen gelten, invers zueinander sind.

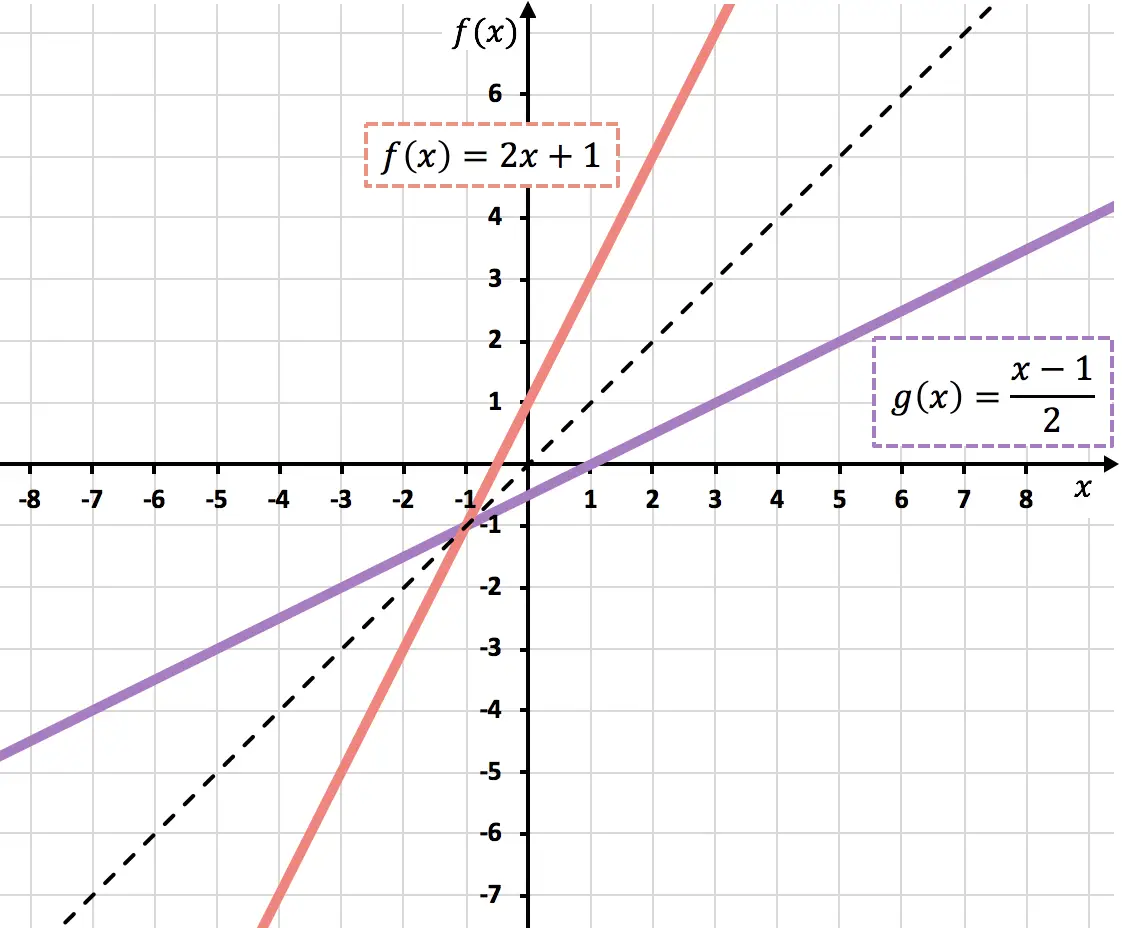
Unten sehen Sie beide Funktionen grafisch dargestellt. Beachten Sie, dass die Graphen zweier Umkehrfunktionen symmetrisch zur Winkelhalbierenden des ersten und dritten Quadranten sind :

So erkennen Sie, ob eine Funktion eine Umkehrung hat

Eine Funktion hat eine Umkehrfunktion, wenn sie eine injektive Funktion ist , das heißt, wenn jeder Wert in ihrem gesamten Definitionsbereich einem einzelnen Wert in ihrem Intervall entspricht.

Exponentialfunktion mit Umkehrfunktion

Quadratische Funktion ohne Umkehrfunktion

Beispielsweise hat die linke Exponentialfunktion eine Umkehrfunktion, da jedes x einem einzelnen Wert von f(x) entspricht. Andererseits hat die rechte quadratische Funktion keine Umkehrfunktion, da sie mehrere Werte von x hat, deren Bilder gleich sind (zum Beispiel f(1)=f(3)=2) .

Ebenso besteht eine bijektive Funktion aus einer Funktion, die sowohl injektiv als auch surjektiv ist, daher hat jede bijektive Funktion auch eine Umkehrfunktion.

Andererseits sollten Sie bedenken, dass es sich bei der Umkehrfunktion nicht um dasselbe wie die multiplikative Umkehrung einer Funktion handelt, sondern um zwei unterschiedliche Konzepte. Um die multiplikative Umkehrung einer Funktion zu finden, berechnen Sie einfach eine Entsprechung dieser Funktion.

$f^{-1}(x) \neq \cfrac{1}{f(x)}$

Im nächsten Abschnitt erfahren Sie, wie Sie die Umkehrfunktion bestimmen.

So finden Sie die Umkehrfunktion

Um die Umkehrung einer Funktion zu berechnen, müssen folgende Schritte durchgeführt werden:

Ersetzen Sie f(x) durch y .
Ändern Sie alle x in y und umgekehrt.
Löschen Sie die y- Variable.
Ersetzen Sie die Variable y durch f ^-1 (x) . Die Umkehrfunktion ist der für f ^-1 (x) gefundene Ausdruck.

Damit Sie genau sehen können, wie die Umkehrfunktion berechnet wird, ermitteln wir beispielhaft die Umkehrfunktion der folgenden Funktion:

$f(x) =4x+5$

Zunächst müssen wir ersetzen

$f(x)$

Für

$y$

$y=4x+5$

Jetzt ändern wir alles

$x$

der Funktion durch

$y$

, und umgekehrt:

$y= 4x+5 \quad \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \quad x= 4y+5$

Dann löschen wir die Variable

$y:$

$x=4y+5$

$x-5=4y$

$\cfrac{x-5}{4}=y$

$y=\cfrac{x-5}{4}$

Und schließlich die Umkehrfunktion von

$f(x)$

ist der algebraische Ausdruck, den wir durch Isolieren erhalten haben

$y:$

$\bm{f^{-1}(x) = } \cfrac{\bm{x-5}}{\bm{4}}$

Gelöste Übungen zur Umkehrfunktion

Nachfolgend haben wir einige Schritt-für-Schritt-Übungen zur Umkehrfunktion vorbereitet, damit Sie sie üben können.

👉 Denken Sie daran: Wenn Sie nicht verstehen, wie man eine Übung löst, oder wenn Sie möchten, dass wir ein Problem für Sie lösen, können Sie uns in den Kommentaren schreiben!

Übung 1

Prüfen Sie, ob die folgenden beiden Funktionen invers (oder reziprok) sind oder nicht:

$f(x)=3x-7\qquad g(x)=\cfrac{x+7}{3}$

Sehen Sie sich die Lösung an

Damit die beiden Funktionen zueinander invers sind, muss Folgendes zutreffen:

$(f \circ g)(x)=x \qquad \qquad (g \circ f)(x)=x$

Es ist daher zu prüfen, ob beide Voraussetzungen erfüllt sind. Wir prüfen zunächst

$(f \circ g)(x)=x :$

$\begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}$

Noch,

$(f \circ g)(x) = x$

ja, es ist geschafft. ✅

Schauen wir uns nun die weitere Zusammensetzung der Funktionen an

$(g \circ f)(x)=x :$

$\begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}$

Wodurch

$(g \circ f)(x) = x$

es ist auch gelungen. ✅

Wie kommt es dazu

$(f \circ g)(x)=x$

Und

$(g \circ f)(x)=x$

, die beiden Funktionen sind Umkehrungen zueinander.

Übung 2

Berechnen Sie die Umkehrfunktion (oder Kehrfunktion) der folgenden Polynomfunktion ersten Grades:

$f(x)=-2x-3$

Sehen Sie sich die Lösung an

Um die Funktion umzukehren, müssen Sie zunächst den Term ersetzen

$f(x)$

Für

$}y:$

$y=-2x-3$

Jetzt ändern wir das

$x$

von

$y$

, und umgekehrt:

$y=-2x-3 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =-2y-3$

Und dann geben wir frei

$y:$

$x =-2y-3$

$x +3=-2y$

$\cfrac{x +3}{-2}=y$

$y = \cfrac{x +3}{-2}$

Die Veröffentlichung ist uns bereits gelungen

$y$

. Daher ist die Umkehrfunktion von

$f(x)$

Ost:

$\bm{f^{-1}(x) = -} \cfrac{\bm{x+3}}{\bm{2}}$

Übung 3

Kehren Sie die folgende quadratische Polynomfunktion um:

$f(x)=x^2-1$

Sehen Sie sich die Lösung an

Um die Umkehrfunktion zu finden, folgen wir dem oben beschriebenen Verfahren. Also werden wir anrufen

$y$

zur Funktion

$f(x):$

$y=x^2-1$

Zweitens ändern wir die

$x$

für die

$y$

, und umgekehrt:

$y=x^2-1 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =y^2-1$

Und schließlich isolieren wir die Variable

$y:$

$x =y^2-1$

$x+1=y^2$

$\sqrt{x+1}=y$

$y=\pm \sqrt{x+1}$

In diesem Fall hat die erhaltene Funktion jedoch zwei Bilder für jedes Element ihrer Domäne (das positive Bild und das negative Bild). Daher gibt es keine Umkehrfunktion der Problemfunktion.

Übung 4

Bestimmen Sie die Umkehrfunktion (oder Kehrfunktion) der folgenden rationalen Funktion:

$\displaystyle f(x)=\frac{x-1}{2x+3}$

Sehen Sie sich die Lösung an

Zuerst ersetzen wir

$f(x)$

Für

$y:$

$y=\cfrac{x-1}{2x+3}$

Jetzt ändern wir das

$x$

Zähler und Nenner

$y$

, und umgekehrt:

$y=\cfrac{x-1}{2x+3} \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x=\cfrac{y-1}{2y+3}$

Und dann geben wir frei

$y:$

$x=\cfrac{y-1}{2y+3}$

Der Ausdruck

$2y +3$

dividiert die gesamte rechte Seite der Gleichung, sodass wir sie multiplizieren können, indem wir die gesamte linke Seite der Gleichung multiplizieren:

$x\cdot (2y+3)=y-1$

$2yx+3x=y-1$

Wir stellen alle Bedingungen mit

$y$

auf der einen Seite der Gleichung und die anderen Terme auf der anderen Seite:

$2yx-y=-3x-1$

Zur Klärung

$}y$

, extrahieren wir den gemeinsamen Faktor von der linken Seite der Gleichung:

$y(2x-1)=-3x-1$

Und als Postbote

$(2x-1)$

besteht darin, die gesamte linke Seite der Gleichung zu multiplizieren. Dies können wir erreichen, indem wir die gesamte rechte Seite dividieren:

$y=\cfrac{-3x-1}{2x-1}$

Die Veröffentlichung ist uns bereits gelungen

$y$

. Also die Umkehrfunktion von

$f(x)$

Ost:

$\bm{f^{-1}(x)=} \cfrac{\bm{-3x-1}}{\bm{2x-1}}$

Eigenschaften der Umkehrfunktion

Die Umkehrfunktion weist folgende Eigenschaften auf:

Die Umkehrfunktion ist eindeutig, das heißt, wenn eine Funktion invertierbar ist, gibt es für diese Funktion nur eine Umkehrfunktion.

Der Bereich der Umkehrfunktion ist der Bereich (oder Bereich) der ursprünglichen Funktion.

Ebenso entspricht der Pfad der Umkehrfunktion dem Definitionsbereich der ursprünglichen Funktion.

Jede aus ihrer Umkehrfunktion zusammengesetzte Funktion ergibt die Identitätsfunktion (x).

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

Der Graph einer Funktion und der Graph ihrer Umkehrfunktion sind symmetrisch zur Winkelhalbierenden des ersten und dritten Quadranten.

Die Umkehrung der Umkehrfunktion ist gleich der ursprünglichen Funktion:

$\left(f^{-1}\right)^{-1}=f$

Das Invertieren einer zusammengesetzten Funktion entspricht der separaten Berechnung der Umkehrung jeder Funktion und der anschließenden Zusammensetzung der Umkehrfunktionen.

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

Eine Funktion ist gleichzeitig stetig mit ihrer Umkehrfunktion, oder anders ausgedrückt: Wenn eine Funktion stetig ist, ist es auch ihre Umkehrfunktion.

Wenn eine Funktion differenzierbar ist und die Ableitung zu keinem Zeitpunkt verschwindet
$f'(x)\neq 0$

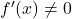
, seine Umkehrfunktion wird auch differenzierbar sein.

Darüber hinaus kann die Ableitung der Umkehrfunktion durch Anwendung des Umkehrfunktionssatzes berechnet werden, dessen Formel lautet:

$\left(f^{-1}\right)'(y)=\cfrac{1}{f'(x)}$

Inverse (oder reziproke) funktion

Was ist die Umkehrfunktion?

Beispiel einer Umkehrfunktion

So erkennen Sie, ob eine Funktion eine Umkehrung hat

So finden Sie die Umkehrfunktion

Gelöste Übungen zur Umkehrfunktion

Übung 1

Übung 2

Übung 3

Übung 4

Eigenschaften der Umkehrfunktion

Kommentar verfassen Kommentieren abbrechen