Auf dieser Seite finden Sie alles über die Umfangsgleichung: gewöhnliche Gleichung, allgemeine Gleichung, andere Arten von Umfangsgleichungen, wann die Umfangsgleichung korrekt ist, … Außerdem sehen Sie Beispiele, wie Sie die Gleichung finden eines Umfanges und Sie können mit gelösten Übungen üben.
Gewöhnliche Kreisgleichung
Bevor wir sehen, was die Umfangsgleichung ist, erinnern wir uns an den Begriff des Umfangs:
Der Umfang ist der Ort der Punkte auf der Ebene, die von einem festen Punkt, dem Mittelpunkt, gleich weit entfernt sind.
Daher haben alle Punkte auf einem Kreis den gleichen Abstand von seinem Mittelpunkt.
Darüber hinaus ist der Kreis neben Ellipse, Parabel und Hyperbel einer der vier Kegelschnitte. Das heißt, ein Kreis kann durch Schneiden eines Kegels mit einer Ebene parallel zu seiner Basis erhalten werden.
Der einfachste Weg, einen Kreis in der kartesischen Ebene zu beschreiben, ist seine gewöhnliche Gleichung. Die Formel für die gewöhnliche Umfangsgleichung lautet also wie folgt:
Die gewöhnliche Kreisgleichung lautet:
Gold:
-
ist der Radius des Kreises.
-
Und
sind die Koordinaten des Kreismittelpunkts:
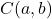
Obwohl wir es nicht demonstrieren werden, weil es etwas mühsam ist, kann diese Gleichung aus dem Satz des Pythagoras abgeleitet werden.
Sehen wir uns anhand eines Beispiels an, wie die gewöhnliche Kreisgleichung berechnet wird:
- Bestimmen Sie die gewöhnliche Gleichung des Kreises mit dem Radius 5, dessen Mittelpunkt der Punkt ist
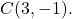
Die Formel für die gewöhnliche Kreisgleichung lautet:
Deshalb müssen wir nur das Unbekannte ersetzen
durch den Wert des Radius und die Unbekannten
Und
durch die Koordinaten X bzw. Y des Kreismittelpunkts:
Die gewöhnliche Kreisgleichung lautet also:
Allgemeine Kreisgleichung
Eine andere Art der Umfangsgleichung ist die allgemeine Gleichung, die tatsächlich am häufigsten verwendet wird. Wir werden dann sehen, wie man die allgemeine Gleichung eines beliebigen Umfangs aus seiner gewöhnlichen Gleichung erhält.
Betrachten Sie die gewöhnliche Kreisgleichung:
Wenn wir die bemerkenswerten Gleichheiten (oder bemerkenswerten Produkte) entwickeln:
Jetzt nehmen wir 3 Variablenänderungen vor:
Und schließlich erhalten wir die allgemeine Gleichung des Umfangs:
Die Formel für die allgemeine Umfangsgleichung lautet daher:
wobei der Mittelpunkt des Kreises ist:
Und der Radius des Kreises ist:
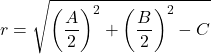
Diese Umfangsgleichung ergibt sich also immer aus der gewöhnlichen Gleichung. Hier ist ein Beispiel, um zu sehen, wie es gemacht wird:
- Bestimmen Sie die allgemeine Gleichung des Kreises mit dem Radius 6, dessen Mittelpunkt der Punkt ist
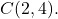
Zuerst müssen wir die gewöhnliche Kreisgleichung finden. Dazu verwenden wir seine Formel:
Und nun operieren wir so lange, bis wir die allgemeine Gleichung des Umfangs gefunden haben, das heißt bis wir nicht mehr vereinfachen können:
Die allgemeine Kreisgleichung lautet also:
Obwohl das Problem dies nicht erforderte, können wir jetzt den Mittelpunkt und den Radius der gefundenen Gleichung berechnen, um zu überprüfen, ob sie korrekt ist.
Um den Mittelpunkt des Kreises zu bestimmen, verwenden wir seine Formel:
Tatsächlich stimmt der Mittelpunkt des Kreises mit dem der Aussage überein.
Wir überprüfen auch den Radius des Umfangs mit seiner Formel:
![\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04dc99d462a8ceb5e6dca936999a4ce8_l3.png "Rendered by QuickLaTeX.com")
Und der Radius ist auch gleich dem der Aussage. Daher ist die berechnete Umfangsgleichung korrekt.
Existenz eines Umfangs
Alle Gleichungen in Form von
entsprechen einem Kreis. Damit diese Art von Ausdruck wirklich die Gleichung eines Kreises ist, müssen die folgenden drei Bedingungen erfüllt sein:
- Die Koeffizienten von
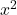
und von
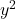
Sie müssen gleich 1 sein. Bedenken Sie, dass die gesamte Gleichung durch diese Zahl dividiert werden könnte, wenn beiden Variablen eine andere Zahl als eins vorangestellt wäre, sie aber beide dieselbe Zahl hätten, sodass ihre Koeffizienten 1 wären.
- Die Gleichung kann keinen Term haben
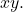
- Der folgende Ausdruck muss positiv sein:
Andere Arten von Kreisgleichungen
Die beiden Kreisgleichungen, die wir gesehen haben, die gewöhnliche Gleichung und die allgemeine Gleichung, werden am häufigsten verwendet, um einen Kreis in der Ebene (im R2) mathematisch auszudrücken. Es gibt jedoch mehrere Arten von Gleichungen zur Beschreibung dieses geometrischen Objekts. Nachfolgend finden Sie eine Erklärung zu jeder dieser Gleichungen.
Kanonische Gleichung des Kreises
Die kanonische Gleichung oder reduzierte Gleichung eines Kreises wird verwendet, um jeden Kreis zu beschreiben, dessen Mittelpunkt im Koordinatenursprung liegt , also im Punkt (0,0). Diese Gleichung lautet wie folgt:
Wenn zusätzlich der Radius der Einheit (1) äquivalent wäre, wäre die Gleichung des Umfangs:
Diese letzte Gleichung entspricht dem goniometrischen Umfang, auch Einheitsumfang oder Einheitskreis genannt. Es ist der Kreis mit dem Radius 1, der im Koordinatenursprung zentriert ist.
Gleichungen zweier konzentrischer Kreise
Zwei konzentrische Gleichungen sind solche, deren Mittelpunkt im selben Punkt liegt. Und der einzige Unterschied zwischen zwei konzentrischen Kreisen ist der Radius.
Damit diese Bedingung erfüllt ist, sind die Gleichungen zweier konzentrischer Kreise bis auf ihre unabhängigen Terme, die unterschiedlich sein müssen, genau gleich.
Beispielsweise sind die folgenden zwei Kreise konzentrisch, da alle ihre Koeffizienten bis auf die unabhängigen Terme identisch sind:
Parametrische Gleichung des Kreises
Wie die Gerade lässt sich auch die Kreisgleichung mit den trigonometrischen Funktionen Sinus und Cosinus parametrisieren. Somit lauten die parametrischen Gleichungen des Kreises:
![\diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)](https://mathority.org/wp-content/ql-cache/quicklatex.com-72dae5b3c5f775661ecb102945bb3fbd_l3.png "Rendered by QuickLaTeX.com")
wo der Punkt
ist der Mittelpunkt des Kreises und
Das ist Ihre Abteilung.
Probleme der Kreisgleichung gelöst
Übung 1
Berechnen Sie die allgemeine Gleichung des Kreises mit dem Radius 5, dessen Mittelpunkt in diesem Punkt liegt
Um die allgemeine Gleichung des Kreises zu finden, müssen wir zunächst seine gewöhnliche Gleichung finden. Dazu verwenden wir die Formel für die gewöhnliche Kreisgleichung:
Sobald wir die gewöhnliche Gleichung kennen, arbeiten wir, bis wir die allgemeine Gleichung des Kreises finden:
Die allgemeine Kreisgleichung lautet also:
Übung 2
Ermitteln Sie für jeden der folgenden Kreise die Koordinaten seines Mittelpunkts und die Länge seines Radius.
Umfang A)
Der Umfang wird in Form einer gewöhnlichen Gleichung ausgedrückt, deren Formel lautet:
Daher sind die Koordinaten des Kreismittelpunkts:
Und sein Radius ist:
Umfang B)
Dieser Umfang wird in Form einer allgemeinen Gleichung ausgedrückt. Um die Koordinaten seines Mittelpunkts zu berechnen, müssen Sie daher die folgende Formel verwenden:
Andererseits lautet die Formel zum Ermitteln des Kreisradius:
![\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0cdc38937e6c36bb9e6d2ca0814a650_l3.png "Rendered by QuickLaTeX.com")
Umfang C)
Der Umfang wird in Form einer gewöhnlichen Gleichung ausgedrückt, deren Formel lautet:
Daher sind die Koordinaten des Kreismittelpunkts:
In diesem Fall hat die Gleichung keinen Term.
weder
es ist daher auf den Koordinatenursprung zentriert:
Und sein Radius ist:
Übung 3
Welche der folgenden Gleichungen ist die Kreisgleichung?
Damit ein Ausdruck die Gleichung eines Kreises ist, müssen die folgenden Bedingungen erfüllt sein:
1. Die Koeffizienten von
und von
Sie müssen gleich 1 sein.
2. Die Gleichung darf keinen Term haben
3.
Wir müssen daher überprüfen, ob die drei Bedingungen für jede Gleichung erfüllt sind.
Gleichung A)
Die Koeffizienten von
Und
sind 1 und die Gleichung hat keinen Term
Es reicht daher aus, die dritte Bedingung zu überprüfen:
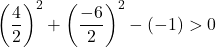
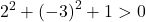
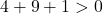
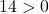Die Gleichung erfüllt die drei Bedingungen, es handelt sich also um die Gleichung eines Kreises.
Gleichung B)
Die Gleichung hat einen Term mit
womit die Gleichung keinem Kreis entspricht.
Gleichung C)
Die Koeffizienten von
Und
sind nicht 1, aber wir können die Gleichung umwandeln, indem wir alle Terme dividieren:
Auf diese Weise sind nun die Koeffizienten von
Und
Ja, sie sind 1 und außerdem hat die Gleichung keinen Term
Wir müssen daher nur die dritte Bedingung bestätigen:
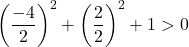
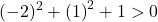
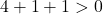
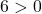Die Gleichung erfüllt die drei Bedingungen, es handelt sich also um die Gleichung eines Kreises.
Gleichung D)
Die Koeffizienten von
Und
sind 1 und die Gleichung hat keinen Term
Es reicht daher aus, die dritte Bedingung zu überprüfen:
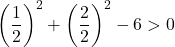
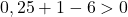
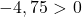Die Gleichung erfüllt die letzte Bedingung nicht, es handelt sich also nicht um die Gleichung eines Kreises .
Übung 4
Bestimmen Sie die Gleichung des Kreises, der durch die folgenden drei Punkte verläuft:
Die allgemeine Gleichung eines beliebigen Kreises lautet:
Daher müssen wir die Koordinaten der Punkte in die Kreisgleichung einsetzen, um die Parameter zu finden
Und
Mit dem ersten Punkt ermitteln wir den Koeffizienten
Mit dem zweiten Punkt ermitteln wir den Koeffizienten
![\begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-12719654d98ba81f0a7d45e587478e6d_l3.png "Rendered by QuickLaTeX.com")
Und ab dem dritten Punkt finden wir den Koeffizienten
![\begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f1e69c28996a8fbfa14189c48a295095_l3.png "Rendered by QuickLaTeX.com")
Zusammenfassend lautet die allgemeine Gleichung für den Umfang:
Übung 5
Wenn die gegenüberliegenden Enden eines Kreises die folgenden zwei Punkte sind:
Wie lautet die gewöhnliche Kreisgleichung?
Wenn die beiden Punkte die Enden des Kreises sind, ist sein Mittelpunkt der Mittelpunkt zwischen diesen beiden Punkten:
Andererseits ist der Durchmesser des Kreises der Abstand zwischen den beiden Punkten, der anhand der Größe des Vektors berechnet werden kann, den die beiden Punkte bilden:
Und der Radius des Kreises ist halb so groß wie der Durchmesser:
Die gewöhnliche Kreisgleichung lautet daher:
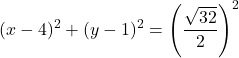
Wenn dieser Artikel für Sie hilfreich war, werden Sie sicherlich auch an unseren Seiten zu Hyperbeln (Mathematik) und Parabeln (Mathematik) interessiert sein. Sie finden eine detaillierte Erklärung, was die Hyperbel und die Parabel sind, ihre Gleichungen, ihre Eigenschaften, Beispiele, gelöste Übungen …