Bereich eines arrays basierend auf einem parameter

Auf dieser Seite erfahren Sie, wie Sie den Rang einer Tabelle anhand eines Parameters berechnen. Außerdem finden Sie Schritt-für-Schritt-Beispiele und gelöste Übungen, wie Sie den Bereich einer Matrix anhand eines Parameters ermitteln.

Um das Verfahren zur Untersuchung des Rangs von Matrizen mit Parametern vollständig zu verstehen, ist es wichtig, dass Sie bereits wissen , wie der Rang einer Matrix anhand von Determinanten berechnet wird . Daher empfehlen wir Ihnen, sich zunächst mit diesen beiden Dingen vertraut zu machen, bevor Sie mit dem Lesen fortfahren.

So berechnen Sie den Bereich eines Arrays basierend auf einem Parameter. Beispiel:

  • Bestimmt den Bereich der Matrix A basierend auf verschiedenen Parameterwerten

    \displaystyle a :

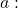
\displaystyle A= \begin{pmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{pmatrix}

Matrix A hat höchstens Rang 3, da es sich um eine Matrix der Ordnung 3 handelt. Daher müssen wir zunächst die Determinante der gesamten 3×3-Matrix mit der Sarrus-Regel lösen, um zu sehen, ob sie Rang 3 erreichen kann:

\displaystyle \begin{aligned} \begin{vmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{vmatrix} & =-a(a+1)+0+0+a+1-0-0 \\ & =-a^2-a+a+1 \\[1.5ex] & =-a^2+1 \end{aligned}

Das Ergebnis der Determinante ist eine Funktion des Parameters

\displaystyle a

. Daher setzen wir das Ergebnis auf 0, um zu sehen, wann die Tabelle Rang 2 und wann Rang 3 hat:

\displaystyle -a^2+1 = 0

Und wir lösen die resultierende Gleichung:

\displaystyle a^2 = 1

\displaystyle \sqrt{a^2} = \sqrt{1}

\displaystyle \bm{a = \pm 1}

Deshalb wann

\displaystyle a

Unabhängig davon, ob es +1 oder -1 ist, ist die 3×3-Determinante 0 und daher ist der Rang der Matrix nicht 3. Andererseits, wann

\displaystyle a

von +1 und -1 verschieden ist, unterscheidet sich die Determinante von 0 und daher hat die Matrix den Rang 3.

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }

Nun wollen wir sehen, was wann passiert

\displaystyle \bm{a=+1} :

\displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & -1 & 2 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & 1 \end{pmatrix}

Wie wir zuvor gesehen haben, wann

\displaystyle a

Ist 1, ist die Determinante der Matrix 0. Sie kann daher nicht den Rang 3 haben. Wir versuchen nun, eine von 0 verschiedene 2×2-Determinante innerhalb der Matrix zu berechnen, zum Beispiel die der oberen linken Ecke:

\displaystyle \begin{vmatrix} 2 & -1 \\[1.1ex] 0 & -1 \end{vmatrix} =-2-0= -2 \neq 0

Die Determinante der Ordnung 2 ist von 0 verschieden. Wenn also der Parameter

\displaystyle a

oder +1, der Rang der Matrix ist 2:

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }

Sobald wir den Bereich der Matrix sehen, wann

\displaystyle a \neq +1,-1

und wann

\displaystyle a=+1

Mal sehen, was wann passiert

\displaystyle \bm{a = -1} :

\displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 0 & -1 & 0 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & -1 \end{pmatrix}

Wie wir am Anfang gesehen haben, wann

\displaystyle a

es -1 und die Determinante der Matrix ist 0. Daher kann sie nicht auf Rang 3 gesetzt werden. Daher sollten wir versuchen, in der Matrix auf eine Determinante von 2×2 zu stoßen, die sich von 0 unterscheidet, beispielsweise die niedrigere Teil der Matrix. LINKS:

\displaystyle \begin{vmatrix} 0 & -1 \\[1.1ex] 1 & -2 \end{vmatrix} = 0-(-1)= 1\neq 0

Die Determinante der Dimension 2 ist von 0 verschieden. Wenn also der Parameter

\displaystyle a

oder -1, der Rang der Tabelle ist 2:

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }

Wir haben daher drei verschiedene Fälle gefunden, in denen der Rang der Matrix A vom Wert abhängt, den der Parameter annimmt

\displaystyle a.

Hier ist die Zusammenfassung :

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \\ & \end{array} }

Nachdem Sie nun wissen, wie Sie den Bereich der parameterabhängigen Matrizen besprechen, können Sie die folgenden Schritt-für-Schritt-Übungen üben. Um sie zu lösen, werden Ihnen sicherlich die Eigenschaften der Determinatoren helfen. Wenn Sie sich also nicht ganz im Klaren darüber sind, empfehle ich Ihnen, zunächst einen Blick auf die verlinkte Seite zu werfen, wo jeder von ihnen anhand von Beispielen erklärt wird.

Probleme mit dem Parameter-basierten Matrixbereich behoben

Übung 1

Studieren Sie den Bereich der folgenden Tabelle basierend auf dem Parameterwert

\displaystyle a :

\displaystyle A=\begin{pmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}

Matrix A wird höchstens Rang 3 haben, da es sich um eine 3×3-Matrix handelt. Daher müssen wir zunächst die Determinante der gesamten Matrix (mit der Sarrus-Regel) lösen, um zu sehen, ob sie Rang 3 haben kann:

\displaystyle \begin{vmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix} =0-8+2a-4a+12-0 =-2a+4

Wir setzen das Ergebnis auf 0, um zu sehen, wann das Array Rang 2 und wann Rang 3 hat:

\displaystyle -2a+4=0

\displaystyle -2a=-4

\displaystyle a=\cfrac{-4}{-2} = 2

Deshalb wann

\displaystyle a

von 2 verschieden ist, wird die Determinante 3×3 von 0 verschieden sein und daher wird der Rang der Matrix 3 sein.

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq 2 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }

Nun wollen wir sehen, was wann passiert

\displaystyle a=2 :

\displaystyle a = 2 \longrightarrow A= \begin{pmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}

\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix}= 0

\displaystyle \begin{vmatrix} 3 & 1 \\[1.1ex] 2 & 2 \end{vmatrix} = 6-2 = 4 \neq 0

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = 2 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }

Wir haben daher zwei Fälle gefunden, in denen der Bereich der Matrix A mit dem Wert variiert, den der Parameter annimmt:

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 2 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 2\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }

Übung 2

Finden Sie den Bereich der folgenden Tabelle basierend auf dem Parameterwert

\displaystyle a :

\displaystyle A=\begin{pmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{pmatrix}

Matrix A wird höchstens Rang 3 haben, da es sich um eine 3×3-Matrix handelt. Daher müssen wir zunächst die Determinante der gesamten Matrix (mit der Sarrus-Regel) lösen, um zu sehen, ob sie Rang 3 haben kann:

\displaystyle \begin{aligned} \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{vmatrix} & =2a-12-2a+2+12-2a^2 \\ &=2-2a^2\end{aligned}

Wir setzen das Ergebnis auf 0, um zu sehen, wann das Array Rang 2 und wann Rang 3 hat:

\displaystyle 2-2a^2=0

\displaystyle -2a^2=-2

\displaystyle a^2=\cfrac{-2}{-2}

\displaystyle a^2=1

\displaystyle a=\pm 1

Deshalb wann

\displaystyle a

von +1 und -1 verschieden ist, unterscheidet sich die 3×3-Determinante von 0 und daher beträgt der Rang der Matrix 3.

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq +1, -1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }

Nun wollen wir sehen, was wann passiert

\displaystyle a=+1 :

\displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{pmatrix}

\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{vmatrix}= 0

\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 1 & 3 \end{vmatrix} = 6-1 = 5 \neq 0

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }

Nun wollen wir sehen, was wann passiert

\displaystyle a=-1 :

\displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}

\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{vmatrix}= 0

\displaystyle \begin{vmatrix} 2 & 2 \\[1.1ex] -1 & 1 \end{vmatrix} =2-(-2) = 4 \neq 0

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }

Wir haben daher drei Fälle gefunden, in denen der Bereich der Matrix A je nach dem Wert variiert, den der Parameter annimmt:

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }

Übung 3

Berechnet den Bereich der folgenden Tabelle basierend auf dem Parameterwert

\displaystyle a :

\displaystyle A=\begin{pmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{pmatrix}

Matrix A wird höchstens Rang 3 haben, da es sich um eine 3×3-Matrix handelt. Daher müssen wir zunächst die Determinante der gesamten Matrix (mit der Sarrus-Regel) lösen, um zu sehen, ob sie Rang 3 haben kann:

\displaystyle \begin{aligned} \begin{vmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{vmatrix} & =(a+1)(a-3) +2+0-5+6(a+1)-0 \\ & = a^2-3a+a-3 +2-5+6a+6 \\[1.5ex] & =a^2+4a\end{aligned}

Wir setzen das Ergebnis auf 0, um zu sehen, wann das Array Rang 2 und wann Rang 3 hat:

\displaystyle a^2+4a=0

Da es sich um eine unvollständige quadratische Gleichung handelt, extrahieren wir einen gemeinsamen Faktor:

\displaystyle a(a+4)=0

Und wir setzen jeden Term gleich 0:

\displaystyle a(a+4)=0 \longrightarrow \begin{cases} \bm{a = 0} \\[2ex] a+4=0 \ \longrightarrow \ \bm{a=-4}\end{cases}

Als Lösungen haben wir 0 und -4 erhalten. Deshalb wann

\displaystyle a

von 0 und -4 verschieden ist, unterscheidet sich die 3×3-Determinante von 0 und daher beträgt der Rang der Matrix 3.

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq 0, -4 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }

Nun wollen wir sehen, was wann passiert

\displaystyle a=0 :

\displaystyle a = 0 \longrightarrow A= \begin{pmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{pmatrix}

\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{vmatrix}= 0

\displaystyle \begin{vmatrix} 1 & 1 \\[1.1ex] 0 & 1 \end{vmatrix} = 1-0 = 1 \neq 0

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = 0 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }

Nun wollen wir sehen, was wann passiert

\displaystyle a=-4 :

\displaystyle a = -4 \longrightarrow A= \begin{pmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{pmatrix}

\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{vmatrix}= 0

\displaystyle \begin{vmatrix} -3 & 1 \\[1.1ex] 0 & 1\end{vmatrix} =-3-0 = -3 \neq 0

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -4 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }

Wir haben daher drei Fälle gefunden, in denen der Bereich der Matrix A je nach dem Wert variiert, den der Parameter annimmt:

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 0,-4 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 0\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -4\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }

Übung 4

Finden Sie die Ausdehnung der folgenden Matrix der Dimension 3×4 entsprechend dem Wert des Parameters

\displaystyle a :

\displaystyle A=\begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&a \end{pmatrix}

Die Matrix A wird höchstens Rang 3 haben, da wir keine 4×4-Determinante berechnen können. Deshalb müssen wir zunächst alle möglichen Determinanten der Ordnung 3 (mit der Regel von Sarrus) auflösen, um zu sehen, ob sie von der Ordnung 3 sein können:

\displaystyle \begin{aligned} \begin{vmatrix} -1&-3&-2\\[1.1ex] 4&12&8\\[1.1ex] 2&6&4 \end{vmatrix} & =-48-48-48+48+48+48 =\bm{0}\end{aligned}

\displaystyle \begin{aligned} \begin{vmatrix} -1&-3&1\\[1.1ex] 4&12&-4\\[1.1ex] 2&6&a \end{vmatrix} & =-12a+24+24-24-24+12a=\bm{0}\end{aligned}

\displaystyle \begin{aligned} \begin{vmatrix} -1&-2&1\\[1.1ex] 4&8&-4\\[1.1ex] 2&4&a \end{vmatrix} & =-8a+16+16-16-16+8a=\bm{0}\end{aligned}

\displaystyle \begin{aligned} \begin{vmatrix} -3&-2&1\\[1.1ex] 12&8&-4\\[1.1ex] 6&4&a \end{vmatrix} & =-24a+48+48-48-48+24a=\bm{0}\end{aligned}

Die Ergebnisse aller möglichen Determinanten der Ordnung 3 sind 0, unabhängig vom Wert

\displaystyle a

. Daher wird die Matrix niemals den Rang 3 haben, da es egal ist, welchen Wert sie annimmt

\displaystyle a

dass es niemals eine andere 3×3-Determinante als 0 geben wird.

Nun versuchen wir es mit Determinanten der Dimension 2 × 2. Allerdings ergeben alle Determinanten der Ordnung 2 ebenfalls 0, mit Ausnahme der folgenden:

\displaystyle \begin{aligned} \begin{vmatrix} 8&-4\\[1.1ex] 4&a \end{vmatrix} & =8a+16 \end{aligned}

Nun setzen wir das Ergebnis gleich 0 und lösen die Gleichung:

\displaystyle 8a+16=0

\displaystyle 8a=-16

\displaystyle a=\cfrac{-16}{8} =-2

Deshalb wann

\displaystyle a

von -2 verschieden ist, wird die Determinante 2×2 von 0 verschieden sein und daher wird der Rang der Matrix 2 sein.

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq -2 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }

Nun wollen wir sehen, was wann passiert

\displaystyle a=-2 :

\displaystyle a = -2 \longrightarrow A= \begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&-2 \end{pmatrix}

Wie wir zuvor gesehen haben, wann

\displaystyle a

ist -2, alle Determinanten der Ordnung 2 sind 0. Sie kann daher nicht vom Rang 2 sein. Und da es mindestens eine 1×1-Determinante gibt, die sich von 0 unterscheidet, ist in diesem Fall der Rang der Matrix 1:

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -2 \ \longrightarrow \ Rg(A)=1} \phantom{33} \\[-2ex] & \end{array} }

Wir haben daher zwei Fälle gefunden, in denen der Bereich der Matrix A mit dem Wert variiert, den der Parameter annimmt:

\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq -2 \longrightarrow \ Rg(A)=2} \phantom{33} \\[3ex] \color{black} \bm{a = -2\ \longrightarrow \ Rg(A)=1} \\ & \end{array} }

Kommentar verfassen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

Nach oben scrollen