Trigonometrische Winkelverhältnisse sind die Verhältnisse, die man aus den drei Seiten eines rechtwinkligen Dreiecks erhält. Mit anderen Worten: Dies sind die Werte, die sich aus dem Vergleich seiner drei Seiten mittels Quotienten (Divisionen) ergeben. Allerdings ist zu beachten, dass diese Gründe nur bei rechtwinkligen Dreiecken (Dreiecken mit einem Winkel von 90°) vorliegen.
Trigonometrische Verhältnisse in einem rechtwinkligen Dreieck
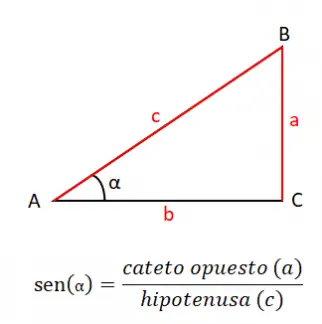
Die sechs wichtigsten trigonometrischen Verhältnisse sind: Sinus, Cosinus, Tangens, Kosekans, Sekante und Kotangens. Als nächstes werden wir im Detail erklären, wie jeder dieser Gründe definiert ist, und wir werden über die Formel sprechen, die sie charakterisiert. Um die folgenden Erklärungen zu verstehen, berücksichtigen wir das folgende rechtwinklige Dreieck:

Brust
Der Sinus eines Winkels (sin oder sin) ist gleich dem Quotienten des Gegenkatheten (a) zwischen der Hypotenuse (c), daher lautet die Sinusformel: sin (α) = a / c . Es ist sehr wichtig, diese Definition des Sinus zu kennen, da sie neben den anderen Gründen, die wir in diesem Abschnitt behandeln werden, die Grundlage aller Trigonometrie ist.
Trav Mit dem Sinussatz können wir jede Seite des Dreiecks berechnen, indem wir die Quotienten eines bestimmten Winkels zwischen den entsprechenden Seiten verbinden. Wenn wir beispielsweise die Seite a berechnen möchten und die Seitenwerte der Winkel A und B haben, können wir dies mit der Formel tun: a / sin (A) = b / sin (B) . Durch Lösen dieser einfachen Gleichung erhalten wir den Wert, der der Variablen entspricht, die wir berechnen möchten.
Kosinus
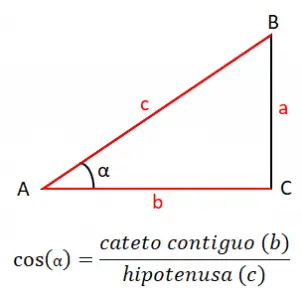
Der Kosinus eines Winkels (cos) ist gleich dem Quotienten des benachbarten Schenkels (b) zwischen der Hypotenuse (c), daher lautet die Kosinusformel: cos (α) = b / c . In diesem Fall besteht die Formel aus den beiden Seiten des Dreiecks, die mit dem Winkel in Kontakt stehen, den wir untersuchen möchten, in diesem Beispiel dem Winkel A oder α.
Mit dem Kosinus haben wir auch eine Möglichkeit, die Seiten des Dreiecks zu berechnen, die aus dem Kosinussatz stammt. Dadurch können wir die Seiten mit den Winkeln verbinden und erhalten die folgenden drei Ausdrücke:
a² = b² + c² – 2bc cos (A)
b² = a² + c² – 2ac cos (B)
c² = a² + b² – 2ab cos (C)
Tangente
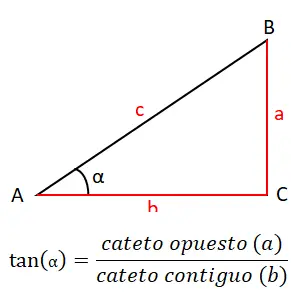
Der drittwichtigste Grund, mit dem wir die Menge der ursprünglichen Gründe abschließen, ist der Tangens (tan oder tg). Dies wird durch Division zwischen dem gegenüberliegenden Bein (a) und dem benachbarten Bein (b) berechnet, daher lautet die Tangensformel: tan (α) = a / b . Sie können es unten grafisch sehen:
Für die Tangente gibt es auch einen eigenen Satz, den sogenannten Tangentensatz. Dadurch können wir die Längen zweier Seiten eines Dreiecks mit den Tangenten der Winkel in Beziehung setzen. Die Aussage lautet wie folgt: „Der Quotient der Summe zweier Seiten zwischen ihrer Subtraktion ist gleich dem Quotienten zwischen dem Tangens des Durchschnitts der beiden Winkel, die diesen Seiten gegenüberliegen, und dem Tangens der halben Differenz dieser Seiten.“
Abgeleitete trigonometrische Verhältnisse
Aus den drei trigonometrischen Verhältnissen, die wir gerade besprochen haben, können wir andere abgeleitete trigonometrische Verhältnisse erhalten. Diese erhält man, indem man das umgekehrte Verhältnis zu Sinus, Cosinus und Tangens bildet.
- Kosekans: ist das Umkehrverhältnis des Sinus und wird mit den Formeln berechnet: cosec (α) = c / a und cosec (α) = 1 / sin (α).
- Sekante: ist das inverse Verhältnis des Kosinus und wird mit den Formeln berechnet: sec (α) = c / b und sec (α) = 1 / cos (α).
- Kotangens: ist das inverse Verhältnis des Tangens und wird mit den Formeln berechnet: cotg (α) = b / a und cotg (α) = 1 / tan (α).
Tabelle der trigonometrischen Verhältnisse
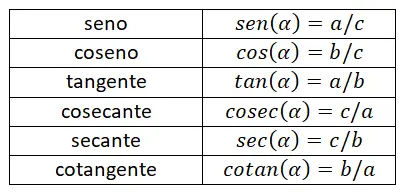
Unten sehen Sie eine Tabelle, die alle bisher erläuterten Gründe zusammenfasst. Mit dieser Tabelle können Sie sich alle Formeln effektiv merken, da Sie so die Unterschiede zwischen den einzelnen mathematischen Ausdrücken leicht unterscheiden können.
Trigonometrische Verhältnisse im Kreis
Eine andere Möglichkeit, die Trigonometrie zu studieren, ist der goniometrische Umfang oder Einheitskreis . Dieser Umfang hat einen Radius gleich 1 und sein Ursprung ist der Punkt (0, 0). Die Zeichnung besteht aus einem Kreis und einem im Kreis dargestellten rechtwinkligen Dreieck. Genauer gesagt muss der Winkel, den wir untersuchen, den ursprünglichen Punkt berühren.
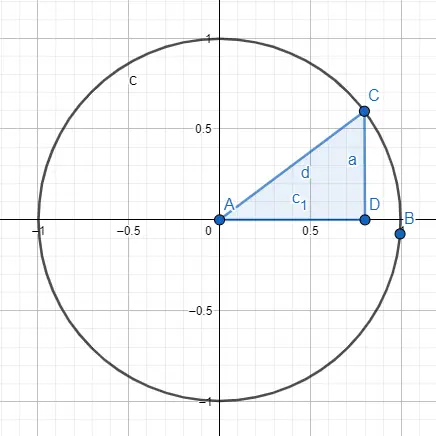
Wenn wir dieses Bild haben, wissen wir, dass der Radius gleich der Hypotenuse ist, die gleich 1 ist. Wenn wir also Sinus und Cosinus berechnen wollen, verwenden wir den Wert des Radius und den Wert der anderen Seiten von das Dreieck. Um den Sinus zu berechnen, führen wir die folgende Berechnung durch: sin (A) = CD / AC = CD / Radius = CD / 1 = CD , also ist der Sinus von A a. Um andererseits den Kosinus zu berechnen, führen wir die Berechnung durch: cos (A) = AD / AC = AD / Radius = AD / 1 = AD , daher ist der Kosinus von A c1.
Es ist sehr wichtig, zwei Dinge im Auge zu behalten. Das erste ist, dass die Verwendung dieses Kreises bei der Untersuchung trigonometrischer Verhältnisse auf die Notwendigkeit zurückzuführen ist, mit Winkeln umzugehen, die größer sind als diejenigen, die mit dem Dreieck untersucht werden können. Beispielsweise kann der Winkel von 150° nicht durch ein einfaches Dreieck untersucht werden, da er zu groß ist. Und zweitens ist zu beachten, dass Sinus und Cosinus niemals Werte größer als 1 und kleiner als -1 annehmen können.
Zeichen trigonometrischer Verhältnisse
Wie bereits erwähnt, verwenden wir für den Umgang mit Winkeln, die größer sind als ein Dreieck, den goniometrischen Umfang. Dazu stellen wir ein Dreieck innerhalb des Kreises genau in einem der vier Quadranten dar, die den Umfang teilen. Im folgenden Bild sehen Sie die dargestellten vier Quadranten.
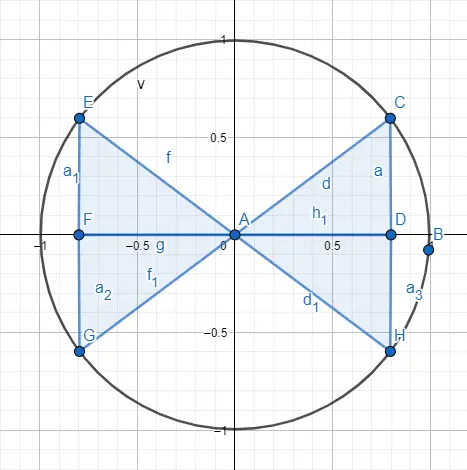
Also, um zwischen einem Winkel von 30 und einem Winkel von 210 zu unterscheiden, die gleich werden bezüglich der Verteilung innerhalb des Dreiecks verwenden wir eine Vorzeichenverteilung entsprechend dem Quadranten, in dem sich das Dreieck befindet. Unten sehen Sie die Schilder für jeden Quadranten und ein gezeichnetes Beispiel.
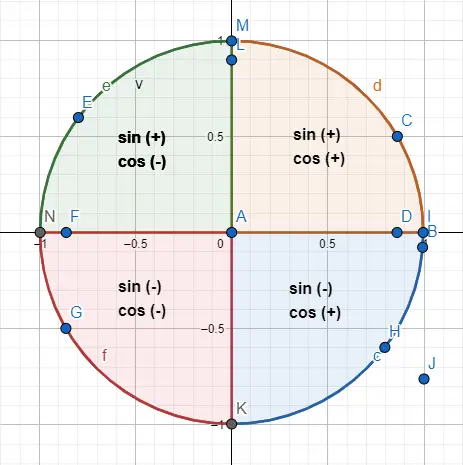
Beispielsweise haben die Winkel 30° und 210° denselben numerischen Wert , aber ihr Sinus und Cosinus haben entgegengesetzte Vorzeichen. Also: sin(30) = 1/2 und cos(30) = √3/2, während sin(210) = -1/2 und cos(210) = -√3/2. Um dieses Ergebnis zu erzielen, stellen wir die beiden Winkel auf dem Umfang dar (Bild unten) und folgen den Hinweisen der Schilder.
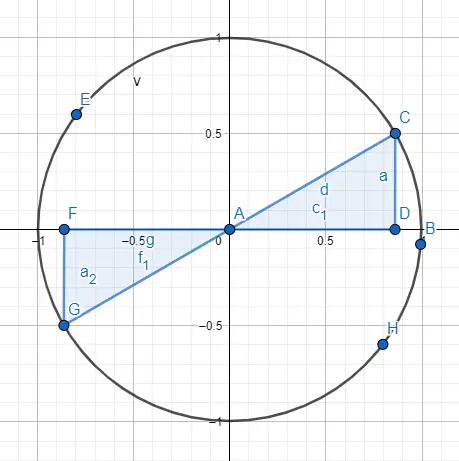
Schließlich, wie es möglich ist , Winkel größer als 360° zu haben, obwohl es vielleicht nicht so aussieht, weil der Umfang nur 360° beträgt. Wenn wir jedoch nach einem Winkel von 750° auflösen wollen, können wir auf einen Winkel zwischen 0° und 360° reduzieren. Wir dividieren einfach 750 durch 360 und der Rest ist der verbleibende Winkel, im Fall von 750° erhalten wir einen Winkel von 30°.
Winkelarten je nach Quadrant
Es gibt Beziehungen zwischen verschiedenen Winkeln, die es uns ermöglichen, die Verhältnisse zu berechnen trigonometrische Werte aller zum Kreis gehörenden Winkel. Lassen Sie uns diese Gründe herausfinden der Reduktion auf den ersten Quadranten . Das bedeutet, dass wir von einem bestimmten Winkel aus eine Vereinfachung zum ersten Quadranten vornehmen und dann die entsprechenden Vorzeichen anbringen. Nachfolgend finden Sie die Erläuterungen zu den unterschiedlichen Vorgehensweisen (abhängig vom Quadranten):
erster Quadrant
In diesem ersten Quadranten (0° – 90°) müssen wir lediglich das trigonometrische Verhältnis mit dem uns vorgegebenen Winkel lösen. Und wenn wir uns das Bild ansehen, das wir zuvor über Symbole erklärt haben, haben Sinus und Cosinus ein Pluszeichen vor sich (das Ergebnis, das wir erhalten, wird durch das Vorzeichen nicht beeinflusst).
Reduktion vom zweiten Quadranten zum ersten
Im zweiten Quadranten (90° – 180°) haben wir es mit Ergänzungswinkeln zu tun, das heißt die beiden Winkel addieren sich zu 180°. Daher müssen wir eine Reduktion vom zweiten Quadranten zum ersten vornehmen und tun dies mit der Formel 180 – α = β , wobei α der Winkel des ersten Quadranten und β der ursprüngliche Winkel ist.
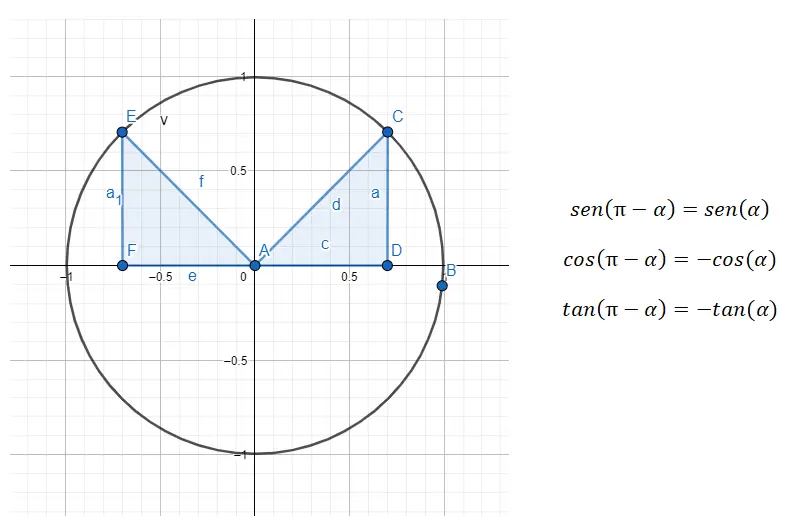
Wenn wir beispielsweise den Winkel 135° erhalten (der zum zweiten Quadranten gehört), müssen wir den Winkel vom ersten Quadranten finden, der mit diesem ersten Quadranten zusammenhängt. In diesem Beispiel beträgt der gesuchte Winkel (α) 45°, da 180 – 45 = 135. Es gilt also: sin (135) = sin (180 – 45) = sin (45), cos (135). ) = cos (180 – 45) = -cos (45) und tan (135) = tan (180 – 45) = -tan (45).
Reduzierung des dritten Quadranten auf den ersten
Im dritten Quadranten (180° – 270°) haben wir es mit Winkeln zu tun, die sich um 80° unterscheiden, was bedeutet, dass die Winkel 180° voneinander entfernt sind. Wenn wir also vom dritten Quadranten zum ersten reduzieren wollen, müssen wir die Formel 180 + α = β verwenden, wobei α der Winkel des ersten Quadranten und β der ursprüngliche Winkel ist.
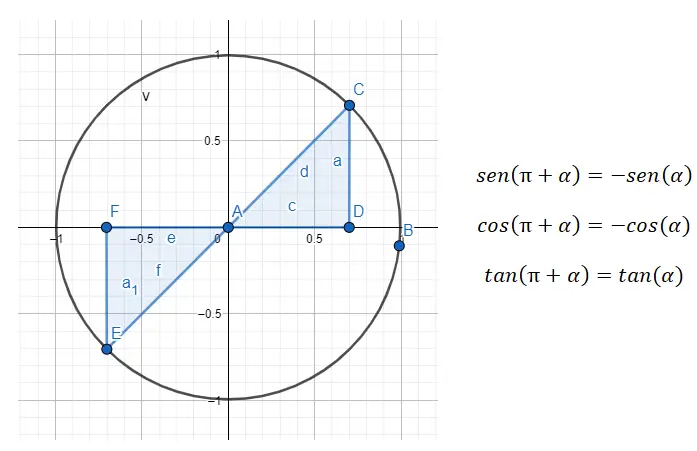
Wenn uns beispielsweise der Winkel 225° gegeben wird (der zum dritten Quadranten gehört), müssen wir den Winkel des ersten Quadranten finden, der ihm entspricht. Im Fall von 225º beträgt der gesuchte Winkel (α) wiederum 45º, da 180 + 45 = 225. Also ist sin (225) = sin (180 + 45) = -sin (45), cos (225) = cos (180 + 45) = -cos (45) und tan (225) = tan (180 + 45) = tan (45) erfüllt sein. ).
Reduzierung des vierten Quadranten auf den ersten
Im vierten Quadranten (270º – 360º) haben wir es mit entgegengesetzten Winkeln zu tun, Das bedeutet, dass die Winkel numerisch gleich sind, aber entgegengesetzte Vorzeichen haben , wie 30° und -30° (entspricht 330°, da 360° – 30° = 330°) . Es ist wichtig zu bedenken, dass entgegengesetzte Winkel als positiver Winkel und negativer Winkel oder als zwei positive Winkel geschrieben werden können (in dem Beispiel, das wir gerade besprochen haben, haben wir den Unterschied erklärt).
Wenn wir also eine Reduktion vom vierten Quadranten zum ersten durchführen wollen, müssen wir die Formel 360 – α = β verwenden, wobei α der Winkel des ersten Quadranten und β der ursprüngliche Winkel ist.
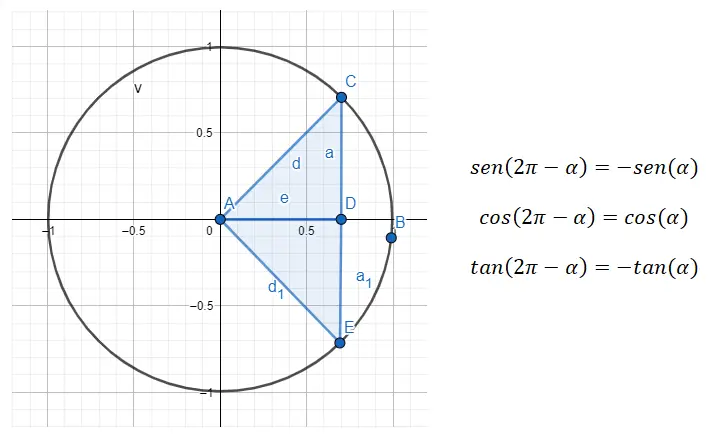
Wenn wir beispielsweise den Winkel 315° erhalten (der zum vierten Quadranten gehört), müssen wir den Winkel des ersten Quadranten finden, der mit diesem ersten Quadranten zusammenhängt. Im Fall des gesuchten Winkels (α) beträgt er immer noch 45°, da 360 – 45 = 315. Also ist sin (315) = sin (360 – 45) = -sin (45), cos ( 315 ) = cos (360 – 45) = cos (45) und tan (315) = tan (360 – 45) = -tan (45). Zusammenfassend haben wir die aus 45° abgeleiteten Winkel aller Quadranten gesehen.
Trigonometrische Verhältnisse der wichtigsten Winkel
Es gibt eine Reihe von Winkeln, sogenannte bemerkenswerte Winkel , die in der Trigonometrie am häufigsten vorkommen. Es wird dringend empfohlen, Ihre trigonometrischen Verhältnisse auswendig zu kennen. Deshalb haben wir unten eine Tabelle erstellt, die die trigonometrischen Verhältnisse dieser Winkel und ihrer Ableitungen (gleiche Winkel, aber mit einem Unterschied von 90, 180 oder 270 Grad) enthält:
| Winkel (°) | Winkel (rad) | Brust | Kosinus | Tangente |
| 0º | 0 rad | 0 | 1 | 0 |
| 30º | 1/6 πrad | 1/2 | √3/2 | √3/3 |
| 45º | 1/4 πrad | √2/2 | √2/2 | 1 |
| 60º | 1/3 πrad | √3/2 | 1/2 | √3 |
| 90º | 1/2πrad | 1 | 0 | ∞ |
| 120º | 5/8πrad | √3/2 | -1/2 | -√3 |
| 135º | 3/4 πrad | √2/2 | -√2/2 | -1 |
| 150º | 5/8πrad | 1/2 | -√3/2 | -√3/3 |
| 180º | πrad | 0 | -1 | 0 |
| 225º | 5/4 πrad | -√2/2 | -√2/2 | 1 |
| 270º | 3/2πrad | -1 | 0 | ∞ |
| 315º | 7/4 πrad | -√2/2 | √2/2 | -1 |
Zusammenhang zwischen trigonometrischen Verhältnissen
Es gibt verschiedene Möglichkeiten, die verschiedenen trigonometrischen Verhältnisse in Beziehung zu setzen. Aus diesen Beziehungen erhalten wir eine Art Gleichheiten zwischen den verschiedenen trigonometrischen Funktionen, die wir trigonometrische Identitäten nennen. Dank dieser Art von Identitäten können wir ein Verhältnis basierend auf jedem anderen berechnen. Es ist zu beachten, dass es viele verschiedene Arten trigonometrischer Identitäten gibt, die auf der Grundlage der Art der Beziehung klassifiziert werden, die den Ausdruck selbst unterstützt.
Trigonometrische Verhältnisse gelöste Probleme
Als nächstes bieten wir Ihnen eine Reihe von Übungen an, mit denen Sie die gesamte in diesem Artikel erläuterte Theorie in die Praxis umsetzen können. Denken Sie daran, dass Sie den Artikel jederzeit noch einmal lesen können, wenn Sie nicht weiterkommen oder Fragen haben. Bei einer zweiten Lektüre werden Sie sicherlich alles viel besser verstehen. Das heißt, Sie können mit dem Üben beginnen:
Übung 1
Berechnen Sie die sechs trigonometrischen Verhältnisse des Winkels 225º:
Wir beginnen mit der Berechnung des Winkels (α), der gleich ist: 180 + α = 225º, also α = 45º.
sin(225) = sin(180 + 45) = -sin(45) = -√2/2
cos(225) = cos(180 + 45) = -cos(45) = -√2/2
tan(225) = tan(180 + 45) = tan(45) = 1
Übung 2
Berechnen Sie die sechs trigonometrischen Verhältnisse des Winkels 120º:
Wir beginnen mit der Berechnung des Winkels (α), der gleich ist: 180 – α = 120º, also α = 60º.
sin(120) = sin(180 – 60) = sin(60) = √3/2
cos(120) = cos(180 – 60) = -cos(60) = -1/2
tan(120) = tan(180 – 60) = -tan(60) = -√3
Übung 3
Berechnen Sie die sechs trigonometrischen Verhältnisse des Winkels 510º:
Bevor Sie beginnen, müssen Sie die Winkelreduzierung vornehmen: 510 / 360 = 1 Umdrehung und ein verbleibender Winkel von 150. Als nächstes berechnen wir den Winkel (α), der gleich ist: 180 – α = 150, also α = 30°.
sin(150) = sin(180 – 30) = sin(30) = 1/2
cos(150) = cos(180 – 30) = -cos(30) = -√3/2
tan(150) = tan(180 – 30) = -tan(30) = -√3/3