Hier erfahren Sie, wie Sie trigonometrische Grenzwerte lösen. Sie können mehrere Beispiele für Grenzen trigonometrischer Funktionen sehen und sogar mit gelösten Schritt-für-Schritt-Übungen zu trigonometrischen Grenzen üben.
Was sind trigonometrische Grenzen?
Trigonometrische Grenzwerte sind Grenzwerte, die anhand trigonometrischer Funktionen berechnet werden. Um trigonometrische Grenzen zu lösen, muss ein Vorverfahren angewendet werden, da sie im Allgemeinen zu Unbestimmtheiten führen.
Darüber hinaus gibt es keine unendlichen Grenzen trigonometrischer Funktionen, da es sich um periodische Funktionen handelt. Das heißt, seine Diagramme werden ständig periodisch wiederholt, ohne auf einen bestimmten Wert zu tendieren.
Formeln für trigonometrische Grenzwerte
Alle trigonometrischen Grenzen werden anhand der folgenden zwei Formeln berechnet:
![]()
Wenn wir versuchen, den Grenzwert durch Substitution zu berechnen, erhalten wir die Nullunbestimmtheit zwischen Null:
![]()
Aber diese trigonometrische Formel kann durch die Berechnung von Werten der näheren Funktion und näher an x=0 (Winkel im Bogenmaß) demonstriert werden.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(-1)=\cfrac{\text{sen}(-1)}{-1}=0,84147\\[3ex]f(-0,1)=\cfrac{\text{sen}(-0,1)}{-0,1}=0,99833\\[3ex]f(-0,01)=\cfrac{\text{sen}(-0,01)}{-0,01}=0,99998\\[3ex]f(-0,001)=\cfrac{\text{sen}(-0,001)}{-0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ccd668acef73b9140a0cbbb9c1d53ad3_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(1)=\cfrac{\text{sen}(1)}{1}=0,84147\\[3ex]f(0,1)=\cfrac{\text{sen}(0,1)}{0,1}=0,99833\\[3ex]f(0,01)=\cfrac{\text{sen}(0,01)}{0,01}=0,99998\\[3ex]f(0,001)=\cfrac{\text{sen}(0,001)}{0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-66152efc3ce1fa761186a65db677af27_l3.png)
Die beiden seitlichen Grenzen der trigonometrischen Funktion ergeben 1, also ist der Grenzwert am Punkt x=0 1:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\\[3ex]\color{orange}\bm{\downarrow}\\[2ex]\lim_{x\to 0}\displaystyle\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8af649189957b154866097e315f7cb92_l3.png)
Somit ist der trigonometrische Grenzwert des Sinus von x dividiert durch x, wenn x gegen 0 tendiert, gleich 1.
Diese Formel kann auch für mehrere Winkel angewendet werden:
![]()
![]()
Wenn wir versuchen, den Grenzwert durch direkte Substitution zu finden, erhalten wir die unbestimmte Form Null zwischen Null:
![]()
Aber wir können die Gleichheit anhand der obigen Formel überprüfen. Dazu müssen Sie zunächst Zähler und Nenner des Bruchs mit 1 plus dem Kosinus von x multiplizieren:
![]()
Wir haben jetzt eine bemerkenswerte Identität im Zähler des Bruchs, sodass wir ihn vereinfachen können:
![]()
![]()
Ausgehend von der grundlegenden trigonometrischen Identität schreiben wir den Zähler um:
![]()
![]()
Wir können den Bruch daher in ein Produkt von Brüchen umwandeln:
![]()
![]()
Mithilfe der Eigenschaften von Grenzwerten können wir den obigen Ausdruck in ein Produkt von Grenzwerten umwandeln:
![]()
Mit der oben gezeigten Formel können wir den trigonometrischen Grenzwert leicht vereinfachen:
![]()
![]()
![]()
Und schließlich berechnen wir den resultierenden Grenzwert:
![]()
Daher wird die trigonometrische Grenzformel überprüft:
![]()
Wie die andere Formel kann sie auch für mehrere Winkel verwendet werden:
![]()
Um trigonometrische Grenzen zu lösen, müssen wir daher Arithmetik verwenden, um die Funktionen umzuwandeln und ähnliche Ausdrücke zu erhalten. Auf diese Weise können wir eine der beiden Formeln verwenden und den Wert des Grenzwerts ermitteln.
Andererseits müssen wir manchmal bestimmte trigonometrische Identitäten anwenden, daher überlassen wir alle unten aufgeführten Formeln Ihnen
Formel, die die drei wichtigsten trigonometrischen Verhältnisse verknüpft:
![]()
Grundlegende trigonometrische Identität:
![]()
Aus der Grundregel abgeleitete trigonometrische Beziehungen:
![]()
![]()
Gegensätzliche Winkel:
![]()
![]()
![]()
Summe zweier Winkel:
![]()
![]()
![]()
Differenz zweier Winkel:
![]()
![]()
![]()
Doppelwinkel:
![]()
![]()
![]()
Halber Winkel:
![]()
![]()
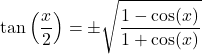
Addition und Subtraktion von Sinus und Cosinus:
![]()
![]()
![]()
![]()
Produkt aus Sinus und Cosinus:
![]()
![]()
![]()
Damit Sie genau sehen können, wie trigonometrische Grenzen berechnet werden, haben wir im Folgenden ein Schritt-für-Schritt-Beispiel zusammengestellt.
Beispiel einer trigonometrischen Grenze
Sehen wir uns anhand des folgenden Beispiels an, wie ein trigonometrischer Grenzwert gelöst wird:
![]()
Beim Versuch, den trigonometrischen Grenzwert zu berechnen, erhalten wir die Unbestimmtheit von Null zwischen Null:
![]()
➤ Siehe: Nullgrenzen zwischen Null
Daher ist es notwendig, die trigonometrische Funktion zu transformieren, um den Grenzwert zu lösen. Die Tangensfunktion ist gleich dem Sinus dividiert durch den Kosinus, also:
![]()
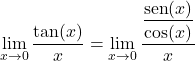
Wir können die Funktion nun als Produkt ausdrücken, indem wir die Eigenschaften von Brüchen anwenden:
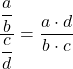
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{\displaystyle\frac{x}{1}}=\lim_{x\to 0}{\frac{\text{sen}(x)\cdot 1}{\text{cos}(x) \cdot x}=\\[6ex]\displaystyle =\lim_{x\to 0}{\frac{\text{sen}(x)}{x\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{1}{\text{cos}(x)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dd10c321c3b7dc40698b318c7187a3c4_l3.png)
Mithilfe der Eigenschaften von Grenzwerten können wir den Grenzwert zweier multiplizierter Funktionen in das Produkt zweier Grenzwerte umwandeln:
![]()
Wie wir oben gezeigt haben, ergibt der erste trigonometrische Grenzwert 1:
![]()
![]()
Führen Sie also einfach die folgende Rechnung durch:
![]()
Gelöste Übungen zu trigonometrischen Grenzen
Übung 1
Lösen Sie den folgenden trigonometrischen Grenzwert:
![]()
Zunächst versuchen wir, den trigonometrischen Grenzwert durch direkte Auswertung zu berechnen:
![]()
Aber wir erhalten eine Null-über-Null-Unbestimmtheit. Wir müssen also Transformationen auf die Funktion anwenden.
Zuerst belassen wir einfach das x im Nenner, indem wir wie folgt vorgehen:
![]()
Jetzt multiplizieren und dividieren wir den Bruch durch 4, um einen Ausdruck zu erhalten, mit dem die erste Formel für trigonometrische Grenzen angewendet werden kann:
![]()
Schließlich wenden wir die eingangs gezeigte Formel an und lösen den trigonometrischen Grenzwert:
![]()
![]()
Übung 2
Berechnen Sie den folgenden trigonometrischen Grenzwert:
![]()
Zuerst versuchen wir, den trigonometrischen Grenzwert zu finden:
![]()
Aber die unbestimmte Form Null entspricht dem Erreichen von Null.
Dann wandeln wir den Tangens in einen Quotienten aus Sinus und Cosinus um:
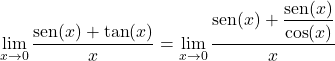
Wir multiplizieren und dividieren mit dem Kosinus von x:
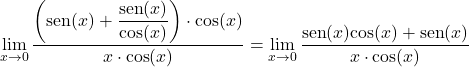
Wir nehmen einen gemeinsamen Faktor im Zähler und teilen den trigonometrischen Grenzwert in zwei Teile:
![]()
Und schließlich finden wir das Ergebnis des trigonometrischen Grenzwerts:
![]()
Übung 3
Lösen Sie den Grenzwert der folgenden trigonometrischen Funktion, wenn x gegen Null geht:
![]()
Durch die direkte Berechnung erhalten wir den unbestimmten Grenzwert 0 zwischen 0:
![]()
Daher vereinfachen wir den Grenzwert, indem wir jeden Term durch den Tangens von x dividieren:
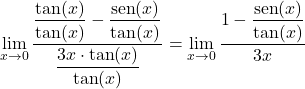
Zweitens können wir aus der grundlegenden trigonometrischen Identität ableiten, dass der Bruchteil des Zählers dem Kosinus von x entspricht:
![]()
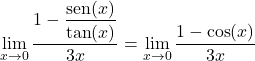
Und indem wir die zweite Formel anwenden, die in der Theorie der trigonometrischen Grenzwerte gezeigt wird, können wir den Grenzwert leicht lösen:
![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}=\lim_{x\to 0}\frac{1}{3}\cdot \frac{1-\text{cos}(x)}{x}=\\[4ex]\displaystyle =\frac{1}{3}\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=\frac{1}{3}\cdot 0=\bm{0}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1ee20bc86ad7559fcda3d6bad3c9b27_l3.png)
Übung 4
Bestimmen Sie die Lösung des folgenden trigonometrischen Grenzwerts am Punkt x=0:
![]()
Wenn wir versuchen, den Grenzwert zu lösen, finden wir die unbestimmte Form 0/0:
![]()
Der algebraische Ausdruck für den Zähler kann unter Verwendung der trigonometrischen Identität des Sinus eines Doppelwinkels umgeschrieben werden:
![]()
![]()
Lassen Sie uns nun den Grenzwert der trigonometrischen Funktion in ein Produkt aufteilen:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)\cdot \text{sen}(5x)}{x\cdot x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc650634075435b782f1e7b921b77c02_l3.png)
Und schließlich lösen wir den trigonometrischen Grenzwert, indem wir die Eigenschaften von Grenzwerten anwenden:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =2\cdot \lim_{x\to 0}\frac{\text{sen}(2x)}{2x}\cdot 5\cdot \lim_{x\to 0}\frac{\text{sen}(5x)}{5x}=\\[4ex]\displaystyle =2\cdot 1\cdot 5\cdot 1=\bm{10}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c26ba3032828541e69e4bd976ac4f96_l3.png)