Hier finden Sie die Erklärung, was sie sind und wie sie alle Teile eines Polynoms (Grad, Variablen, unabhängiger Term usw.) heißen. Darüber hinaus können Sie mehrere Beispiele sehen und Teile eines Polynoms mit gelösten Aufgaben üben.
Aber bevor wir sehen, was alle Teile eines Polynoms sind, schauen wir uns kurz seine mathematische Definition an, um das Konzept vollständig zu verstehen: Ein Polynom ist ein algebraischer Ausdruck, der durch Addition oder Subtraktion von Monomen unterschiedlichen Grades gebildet wird.
Aus welchen Teilen besteht ein Polynom?
Die Teile eines Polynoms sind:
- Begriffe : jeder Monomteil des Polynoms.
- Koeffizienten : die Zahlen, die jeden Term des Polynoms begleiten.
- Grad : Der größte Exponent, auf den die Polynomvariable angehoben wird.
- Variable : ist der Buchstabe, den das Polynom hat.
- Hauptterm : ist der Term höchsten Grades des Polynoms.
- Unabhängiger Term : Term des Polynoms, der keine Variable enthält.
- Dominanter Koeffizient : Koeffizient des dominanten Termes des Polynoms.
Wenn das Polynom nur eine Variable hat, ist sein Grad gleich dem größten Exponenten seiner Terme. Wenn das Polynom jedoch zwei oder mehr Variablen hat, ist es schwieriger, seinen Grad zu ermitteln, da eine Operation durchgeführt werden muss. Erfahren Sie, wie das geht, indem Sie auf den folgenden Link für den Grad eines Polynoms aus zwei (oder mehr) Variablen klicken.
So identifizieren Sie die Teile eines Polynoms
Die Teile oder Elemente eines Polynoms können visuell leicht gefunden werden. Sehen Sie im folgenden Diagramm, wie das geht:
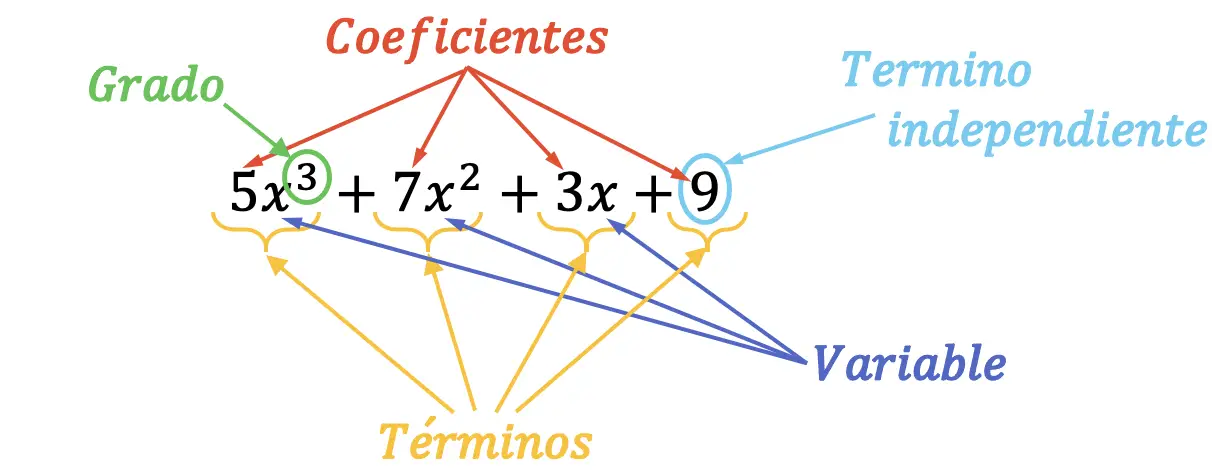
Beim vorherigen Polynom dritten Grades sind alle Teile markiert. Darüber hinaus beträgt der Hauptterm dieses Polynoms ungefähr 5x 3 , da es sich um das Monom höchsten Grades handelt. Ebenso ist der führende Koeffizient des Polynoms 5, da es sich um den Koeffizienten des führenden Termes handelt.
In diesem Fall hat das Polynom eine einzige Variable und daher nur einen Gradtyp. Aber Sie sollten wissen, dass Sie, wenn das Polynom multivariabel ist, zwischen dem absoluten Grad und dem relativen Grad einer Variablen unterscheiden müssen. Sie können sehen, woraus jeder von ihnen besteht, in dem Link, den ich Ihnen oben hinterlassen habe ⬆⬆ ( Grad eines Polynoms zweier Variablen ).
Beispiele für Teile eines Polynoms
Um die Bedeutung der Teile eines Polynoms und die Funktion, die sie erfüllen, vollständig zu verstehen, sehen wir uns einige Beispiele für die Bestimmung der Teile eines beliebigen Polynomtyps an:
Beispiel 1
Identifizieren Sie die Teile des folgenden quadratischen Polynoms (Grad 2):
![]()
- Begriffe: 4x 2 , -8x, 1
- Koeffizienten: 4, -8, 1
- 2. Jahr
- Variable: x
- Hauptbegriff: 4x 2
- Unabhängiges Mandat: 1
- Lenkkoeffizient: 4
Andererseits ist zu beachten, dass das Polynom in diesem Beispiel als Trinom bezeichnet wird. Sie können anhand von Beispielen für Trinome sehen, was dieser Polynomtyp ist. Darüber hinaus könnten Sie auch an einer anderen Art von Polynom namens Binomial interessiert sein (es ist einfacher, einige Operationen damit durchzuführen). Was das Besondere daran ist, können Sie in Binomialbeispielen sehen.
Beispiel 2
Finden Sie die Teile des folgenden Polynoms:
![]()
- Begriffe: y 3 , 9y 2 , -5y, 3
- Koeffizienten: 1, 9, -5, 3
- 3. Jahr
- Variablen: und
- Hauptbegriff: und 3
- Unabhängiges Mandat: 3
- Lenkkoeffizient: 1
Wie Sie in diesem Beispiel sehen können, bedeutet dies, dass der Koeffizient eins ist, wenn vor einem Monom keine Zahl steht. Der führende Koeffizient dieses Polynoms ist also gleich 1.
Gelöste Aufgaben zu den Teilen eines Polynoms
Damit Sie sich die Namen aller Teile eines Polynoms besser merken können, haben wir mehrere gelöste Übungen für Sie vorbereitet. Alle Ihre Fragen dazu können Sie uns in den Kommentaren stellen. ⬇⬇
Übung 1
Finden Sie alle Teile des folgenden Polynoms:
![]()
Das Polynom in dieser Übung hat keinen unabhängigen Term, da alle Terme durch mindestens eine Variable (oder einen Buchstaben) gebildet werden.
Begriffe: 2×4 , 6×2 , x
Koeffizienten: 2, 6, 1
Level 4
Variable: x
Hauptbegriff: 2×4
Unabhängiger Begriff: nicht
Lenkkoeffizient: 2
Übung 2
Finden Sie alle Teile des folgenden Polynoms:
![]()
Das Polynom in diesem Problem besteht aus zwei Variablen: x und y. Noch:
Begriffe: -7x 4 y 2 , 3x 4 , -5y 2 , xy, -10
Koeffizienten: -7, 3, -5, 1, -10
6. Jahr
Variablen: x, y
Hauptbegriff: -7x 4 und 2
Unabhängiges Mandat: -10
Lenkkoeffizient: -7
Wie Sie sehen, müssen Sie zum Lösen solcher Polynome wissen, wie der Grad eines Polynoms mit mehr als einer Variablen berechnet wird. Wenn Sie immer noch nicht sicher sind, wie das geht, empfehle ich Ihnen, den Link oben im Abschnitt „Was sind die Teile eines Polynoms?“ zu lesen. ( Grad eines Polynoms zweier Variablen ). ⬆⬆ Hier finden Sie die Schritt-für-Schritt-Erklärung sowie mehrere Beispiele.
Obwohl es sich um ein völlig anderes Konzept handelt, werden Sie, wenn Sie bis hierher gekommen sind, sicherlich auch daran interessiert sein, den Polynomausdruck einer Zahl zu kennen. Das ist etwas, was nicht viele Leute wissen, aber tatsächlich sehr nützlich ist.