Tartaglias (oder pascals) dreieck

Auf dieser Seite erklären wir, was das Tartaglia-Dreieck, auch Pascal-Dreieck genannt, ist. Wir lernen, wie man das Tartaglia-Dreieck (oder Pascal-Dreieck) mathematisch konstruiert, wofür es verwendet wird und welche Eigenschaften es hat. Abschließend zeigen wir, wie und wann dieses sehr wichtige Dreieck entstand.

Was ist das Dreieck von Tartaglia (oder Pascal)?

Das Tartaglia-Dreieck , auch Pascalsches Dreieck genannt, ist eine mathematische Darstellung geordneter ganzer Zahlen in Form eines Dreiecks. Das Tartaglia-Dreieck (oder Pascal-Dreieck) wird für mathematische Berechnungen verwendet.

Dies ist die Definition des Tartaglia- oder Pascal-Dreiecks, aber Sie verstehen das Konzept sicherlich besser, wenn Sie sich ein Bild des Dreiecks ansehen:

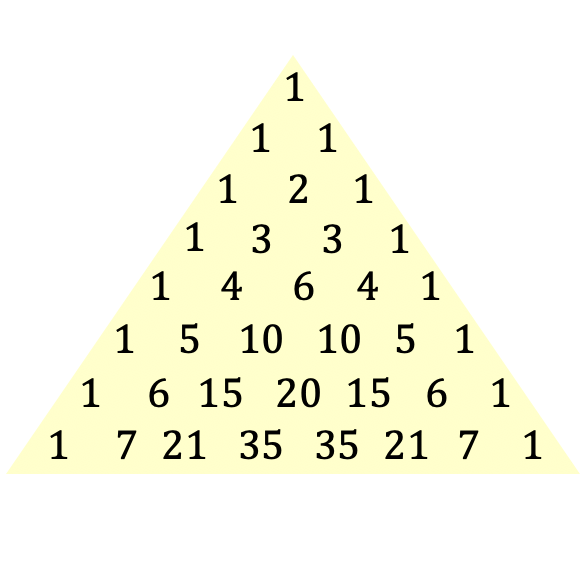
Das Tartaglia-Dreieck wird nach dem französischen Philosophen und Mathematiker Blaise Pascal, der diesen Dreiecksausdruck 1654 einführte, auch Pascal-Dreieck genannt, obwohl dieses Dreieck bereits seit der Antike bekannt ist. Im Folgenden befassen wir uns mit der Geschichte dieses besonderen Dreiecks.

Wie ist das Dreieck von Tartaglia oder Pascal aufgebaut?

Wie Sie in Pascals Dreieck (oder Tartaglia) gesehen haben, gibt es viele Zahlen, aber das bedeutet nicht, dass wir sie auswendig können müssen (Gott sei Dank). Es gibt eine Formel, mit der Sie ganz einfach alle Zahlen im Pascal- oder Tartaglia-Dreieck finden können. Sie müssen lediglich einfache Summen lösen.

Um das Tartaglia- oder Pascal-Dreieck zu konstruieren, beginnen Sie am oberen Ende des Dreiecks, das immer eine 1 ist, und berechnen dann die Linien darunter. Jede Zahl in den folgenden Zeilen ist die Summe der beiden Zahlen direkt darüber, mit Ausnahme der Enden der Zeilen, die immer 1 sind.

Daher können Sie beliebig viele Linien des Tartaglia-Dreiecks berechnen, da Sie durch Addition der Zahlen nacheinander Linien hinzufügen können.

Wofür wird das Dreieck von Tartaglia oder Pascal verwendet?

Zu wissen, wie man das Tartaglia-Dreieck konstruiert, ist sehr gut, aber… wofür wird dieses arithmetische Dreieck verwendet? Nun, das Dreieck von Tartaglia (oder Pascal) hat viele Anwendungen in der Mathematik, insbesondere im Bereich der Algebra.

kombinatorische Zahlen

Zunächst dient das Tartaglia-Dreieck zur direkten Berechnung kombinatorischer Zahlen , auch Binomialkoeffizienten genannt. Wenn Sie nicht wissen, was diese Art von Vorgängen sind, können Sie auf unserer Website danach suchen (wir haben oben rechts eine Suchmaschine), denn wir haben einen ausführlichen Artikel geschrieben, in dem wir Ihnen erklären, wie sie gelöst werden Außerdem finden Sie Beispiele und Übungen, die Schritt für Schritt gelöst werden. Aber zusammenfassend lautet der algebraische Ausdruck für eine kombinatorische Zahl wie folgt:

Nun, alle kombinatorischen Zahlen lassen sich leicht mit dem Tartaglia-Dreieck bestimmen, da die Lösung jedes Binomialkoeffizienten einer Zahl dieses Dreiecksausdrucks entspricht, wie in der folgenden Abbildung dargestellt:

Zum Beispiel die kombinatorische Zahl

gibt 6 zurück, da im Tartaglia-Dreieck stattdessen eine 6 steht.

Wenn Sie also wissen, wie man das Dreieck von Tartaglia oder Pascal konstruiert, können Sie jede kombinatorische Zahl schnell und ohne Verwendung ihrer Formel berechnen.

Newtons Binomial

Eine weitere Verwendung des Tartaglia-Dreiecks (oder Pascal-Dreiecks) besteht darin, Potenzen von Binomialen berechnen zu können (klicken Sie auf diesen Link, um herauszufinden, was ein Binomial ist).

Ein Beispiel für die Potenzierung eines Binomials sind bemerkenswerte Identitäten wie:

Bemerkenswerte Identitäten sind für die Mathematik sehr wichtig, da sie es uns ermöglichen, viele Berechnungen einzusparen und komplizierte Operationen direkt und schnell zu lösen. Deshalb empfehlen wir Ihnen, den folgenden Link zu lesen, wenn Sie noch nicht wissen , was Notable Identities sind .

Wie Sie im vorherigen Link gesehen haben, können bemerkenswerte Produkte direkt mit ihren Formeln gelöst werden. Aber… was passiert, wenn das Paar auf den Würfel oder auf einen höheren Grad angehoben wird?

Nun, diese Binome können mit dem Tartaglia-Dreieck dank des Binomialsatzes (oder Newtons Binomial) auf sehr einfache Weise berechnet werden. Sobald Sie die Methode beherrschen, lässt sie sich schnell anwenden. Um sie gut zu erklären, benötigen Sie eine ganze Seite. Wenn Sie also mehr daran interessiert sind, wie man diese Art von Binomialen löst, klicken Sie auf die verlinkte Seite und Sie können sehen, wie es geht.

Kombinatorik

Auch das Tartaglia-Dreieck oder Pascal-Dreieck kann zur Bestimmung von Kombinationen und Wahrscheinlichkeiten verwendet werden.

Wenn wir jemals auf ein Problem stoßen, bei dem wir bestimmen müssen, wie viele verschiedene Gruppen unabhängig von der Reihenfolge aus einer Gruppe gebildet werden können, können wir das Tartaglia-Dreieck verwenden.

Wenn wir beispielsweise 5 Karten haben, gehen Sie einfach zur dritten Spalte (die erste Spalte ist Null) der fünften Reihe (die erste Reihe ist auch Reihe 0) des Tartaglia-Dreiecks, um zu erfahren, auf wie viele Arten wir 3 auswählen können. Die Zahl an dieser Stelle (10) entspricht der Anzahl der Möglichkeiten, 3 Karten auszuwählen.

So können aus 5 Karten 10 verschiedene Dreiergruppen gebildet werden.

Eigenschaften des Tartaglia- oder Pascal-Dreiecks

Das Tartaglia-Dreieck, auch Pascal-Dreieck genannt, weist folgende Eigenschaften auf:

• Das Tartaglia-Dreieck (oder Pascal-Dreieck) ist symmetrisch, das heißt, die vertikale Linie, die das gesamte Dreieck in zwei gleiche gleichseitige Dreiecke teilt, ist eine Symmetrieachse.

• Die horizontale Summe aller Zahlen in jeder Geraden des Pascalschen Dreiecks entspricht einer Potenz von 2.

• Wichtig sind auch die Diagonalen des Tartaglia-Dreiecks: Die Zahlen auf der ersten Diagonale (Außendiagonale) sind Einsen, die zweite Diagonale wird durch die Folge aller natürlichen Zahlen gebildet, die dritte Diagonale entspricht Dreieckszahlen und die vierte Diagonale ist zusammengesetzt von tetragonalen (oder tetraedrischen) Zahlen.

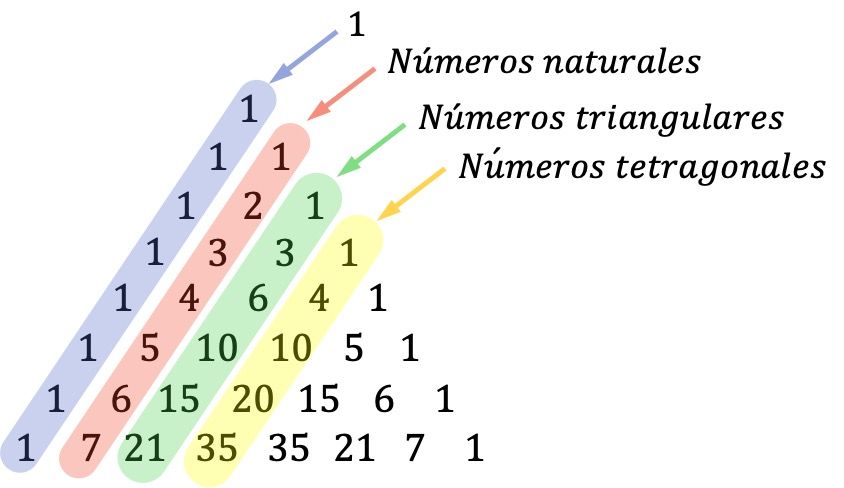
Dreieckszahlen sind Zahlen, die in Form eines Dreiecks dargestellt werden können. Und tetragonale Zahlen sind diejenigen, die dreieckige Pyramiden bilden.

Wenn Sie nicht wissen, was dreieckige oder tetragonale Zahlen sind, passiert nichts, es ist nur eine Kuriosität über das Tartaglia-Dreieck. Sie müssen jedoch die Bedeutung natürlicher Zahlen (Zahlen zum Zählen von Elementen) kennen.

• Wenn die erste Zahl in einer Zeile mit Ausnahme der Zahl 1 eine Primzahl ist, sind alle Zahlen in derselben Zeile durch diese Zahl teilbar. Beispielsweise können in der achten Zeile (1-7-21-35-35-21-7-1) die Zahlen 7, 21 und 35 durch 7 geteilt werden (sieben ist eine Primzahl).

• Eine weitere Besonderheit des Tartaglia-Dreiecks besteht darin, dass die Fibonacci-Reihe durch Addition der Diagonalen auf eine bestimmte Weise gefunden werden kann:

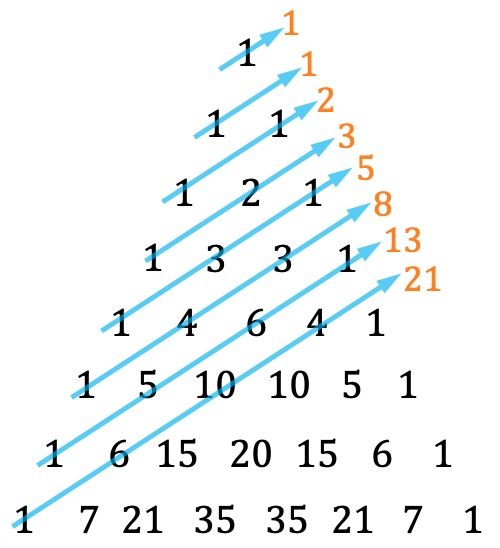
Denken Sie daran, dass jeder Term der Fibonacci-Folge gleich der Summe der beiden vorherigen ist, wobei die ersten beiden Terme 1 und 1 sind. Die Zahlen, die zur Fibonacci-Folge gehören, sind also: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144, 233,…

• Wenn wir zwei aufeinanderfolgende Zahlen aus der dritten Diagonale des Pascalschen Dreiecks (1-3-6-10-15-…) addieren, erhalten wir ein perfektes Quadrat (1, 4, 9, 16, 25,…).

• Wenn wir die geraden Zahlen des Pascalschen Dreiecks in einer Farbe und die ungeraden Zahlen in einer anderen Farbe malen, erhalten wir die Figur des Sierpinski-Dreiecks, einer berühmten geometrischen Menge. Unten sehen Sie das Pascalsche Dreieck mit einer Höhe von 512, dargestellt mit den ungeraden Zahlen in Schwarz und den geraden Zahlen in Weiß:

• Die Singmaster-Vermutung besagt, dass die Häufigkeit, mit der jede Zahl größer als 1 auftritt, endlich ist. Mit anderen Worten: Obwohl die Anzahl der Reihen im Tartaglia-Dreieck unendlich ist, ist die Häufigkeit, mit der jede Zahl außer 1 vorkommt, endlich. Kurioserweise ist die Zahl 3003 die einzige bisher bekannte Zahl, die bis zu acht Mal im Dreieck vorkommt.

Geschichte des Tartaglia- oder Pascal-Dreiecks

Nachdem wir nun wissen, wie das Tartaglia-Dreieck aussieht, wollen wir sehen, wann dieses ganz besondere mathematische Dreieck erfunden wurde.

Obwohl der Name des arithmetischen Dreiecks hauptsächlich den berühmten Wissenschaftlern Tartaglia und Pascal zugeschrieben wird, wurde dieses algebraische Dreieck bereits früher verwendet.

Die erste Aufzeichnung eines aus Binomialkoeffizienten gebildeten Dreiecks stammt aus dem 10. Jahrhundert in Indien. Allerdings begannen die Perser, insbesondere die Mathematiker Al-Karaji (953-1029) und Omar Khayyam (1048-1131), mit der Erforschung seiner Eigenschaften. Aus diesem Grund wurde es im Iran als Khayyam-Pascal-Dreieck oder einfach als Khayyam-Dreieck populär gemacht.

Dieses Dreieck wurde im 11. Jahrhundert vom Mathematiker Jia Xian in China eingeführt, aber erst später im 13. Jahrhundert führte Yang Hui es als arithmetisches Dreieck ein. Und aus diesem Grund nennt man es in dem asiatischen Land das Yang-Hui-Dreieck .

Das mathematische Dreieck gelangte später durch den Deutschen Petrus Apianus auf den europäischen Kontinent, der im Jahr 1527 in seinem Buch Rechnung veröffentlichte. Von dort aus untersuchte der berühmte italienische Algebraist Niccolò Fontana Tartaglia das Dreieck in der ersten Hälfte des 16. Jahrhunderts eingehend und ihm zu Ehren ist es in Ländern wie Italien als Tartaglia-Dreieck bekannt.

Schließlich demonstrierte der Franzose Blaise Pascal viele der untersuchten Eigenschaften des Dreiecks in seiner Veröffentlichung der Abhandlung über das arithmetische Dreieck im Jahr 1654, daher der Name Pascal-Dreieck. Es sei darauf hingewiesen, dass einige dieser Eigenschaften bereits bekannt waren, aber es war Pascal, der ihren Nachweis durch mathematische Induktion führte.