Tangentengleichung -

In diesem Artikel erfahren Sie , wie Sie die Gleichung der Tangente an eine Kurve finden . Darüber hinaus können Sie mit gelösten Übungen unterschiedlicher Schwierigkeitsgrade trainieren.

Gleichung der Tangente an eine Funktion in einem Punkt

Die Gleichung der Tangente an die Funktion f(x) im Punkt x=x ₀ lautet:

$y -y_0= m(x-x_0)$

Wobei der Punkt P(x ₀ ,y ₀ ) der Punkt ist, an dem die Tangente und die Funktion zusammenfallen. Und die Steigung der Tangente m ist gleich der Ableitung der Kurve am Punkt x ₀ , d. h. m=f'(x ₀ ).

Im Bild oben sehen Sie eine Kurve

$f(x)$

dargestellt in Blau und einer orangefarbenen Tangente an die Funktion

$f(x)$

$x=x_0$

, da sie nur diesen Punkt gemeinsam haben. Nun, die Gleichung dieser Tangente lautet

$y -y_0= m(x-x_0)$

und seine Steigung ist

$m=f'(x_0)$

So finden Sie die Tangentengleichung

Um die Tangentengleichung an eine Funktion an einem Punkt zu finden, müssen Sie Folgendes tun:

Ermitteln Sie die Steigung der Tangente, indem Sie die Ableitung der Funktion am Tangentenpunkt berechnen.
Bestimmen Sie einen Punkt auf der Tangente.
Finden Sie die Gleichung der Tangente unter Verwendung der berechneten Steigung und des Punktes der Tangente.

Beispiel für die Gleichung der Tangente an eine Kurve

Nachdem wir die Theorie der Tangentengleichung kennengelernt haben, sehen wir uns an, wie man die Tangentengleichung berechnet, indem wir Schritt für Schritt ein Beispiel lösen:

Berechnen Sie die Gleichung der Tangente an die Kurve
$f(x)=x^2+x$

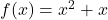
Um

$x=1$

.

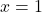
Wir wissen, dass die Tangentengleichung immer die folgende Form hat:

$y -y_0= m(x-x_0)$

Als erstes muss die Steigung der Geraden berechnet werden. Somit ist die Steigung der Tangente,

$m$

, wird der Wert der Ableitung der Kurve am Tangentialpunkt x=1 sein, d. h

$m=f'(1).$

Daher differenzieren wir die Funktion und berechnen dann

$f'(1):$

$f(x)=x^2+x \quad \longrightarrow \quad f'(x)=2x+1$

$f'(1)= 2\cdot 1+1=2+1=3$

$m=f'(1)=3$

Sobald wir den Wert kennen

$m$

, wir müssen einen Punkt finden

$(x_0,y_0)$

der Tangente, um die Tangentengleichung zu vervollständigen.

Die Tangentengleichung und die Kurvengleichung haben immer einen gemeinsamen Punkt , der in diesem Fall der ist

$x=1$

. Daher wie die Kurve

$f(x)$

durch diesen Punkt geht, können wir die andere Komponente des Punktes durch Berechnung ermitteln

$f(1):$

$f(x)=x^2+x$

$f(1)=1^2+1=2$

Der Tangentenpunkt ist also:

$P(1,2)$

Sowohl die Kurve als auch die Tangente verlaufen durch diesen Punkt, sodass wir ihn auch verwenden können, um die Gleichung der Tangente zu finden.

Es bleibt nur noch, die gefundenen Werte der Steigung und des Tangentenpunkts in seine Gleichung einzusetzen:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)$

Kurz gesagt lautet die Tangentengleichung:

$\bm{y-2=3(x-1)}$

Sie können die Tangentengleichung auch mit der expliziten Geradengleichung ausdrücken:

$\bm{y=3x-1}$

Unten sehen Sie die dargestellte Kurve

$f(x)=x^2+x$

und seine Tangente an

$x=1,$

$y-2=3(x-1):$

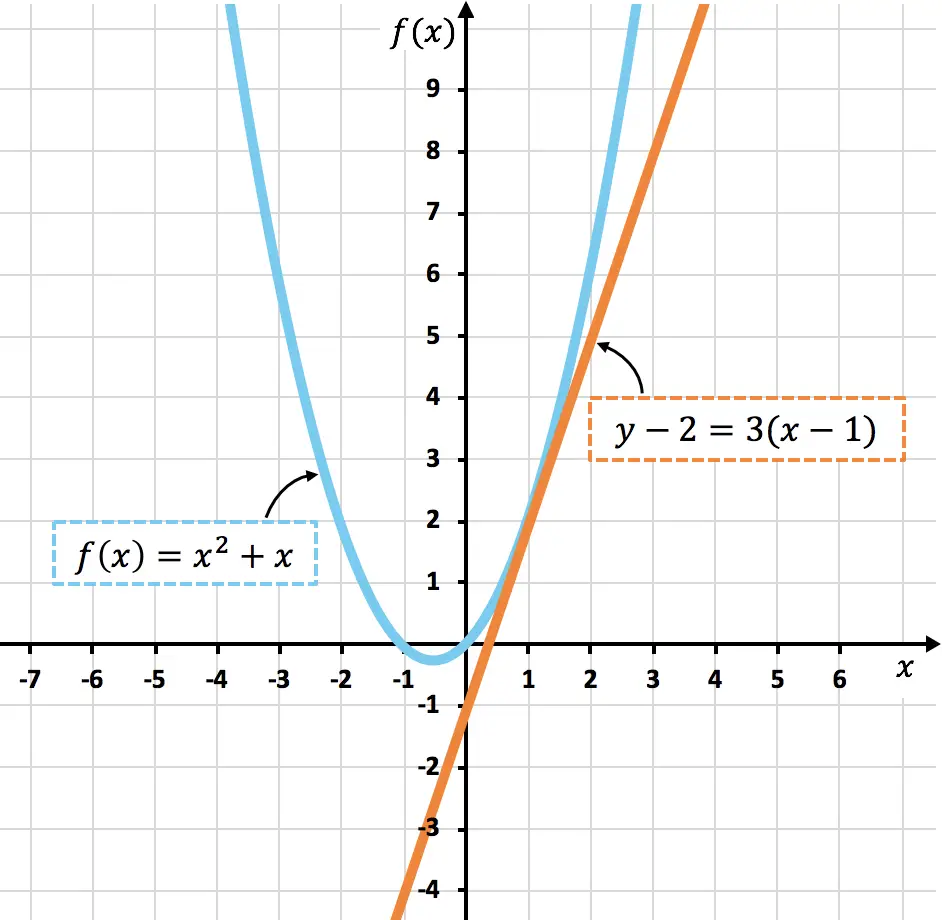
Gleichung einer Tangente an eine Kurve an einem Punkt

Wie Sie sehen können, die Kurve

$f(x)=x^2+x$

und die Tangente

$y-2=3(x-1)$

Sie haben nur den Punkt gemeinsam

$(1,2)$

, genau wie wir es berechnet haben.

Aufgaben zur Tangentengleichung gelöst

Übung 1

Berechnen Sie die Gleichung der Tangente an die Kurve

$f(x)=2x^2-4x+3$

$x=2 .$

Sehen Sie sich die Lösung an

Die Tangentengleichung hat immer die folgende Form:

$y-y_0=m(x-x_0)$

Schritt 1: Berechnen Sie die Steigung der Tangente

Die Steigung m ist der Wert der Ableitung der Kurve am Tangentialpunkt. Daher in diesem Fall

$m = f'(2):$

$f(x)=2x^2-4x+3 \ \longrightarrow \ f'(x)= 4x-4$

$f'(2)= 4\cdot 2-4=8-4=4$

$m=f'(2)=4$

Schritt 2: Suchen Sie einen Punkt auf der Tangente

Die Tangentengleichung und die Kurvengleichung haben immer einen gemeinsamen Punkt, der in diesem Fall der ist

$x=2$

. Daher wie die Kurve

$f(x)$

durch diesen Punkt geht, können wir die andere Komponente des Punktes durch Berechnung ermitteln

$f(2):$

$f(x)=2x^2-4x+3$

$f(2)=2\cdot 2^2-4\cdot 2+3 =2 \cdot 4 -8 +3 = 3$

Somit ist der Punkt, durch den sowohl die Kurve als auch die Tangente verlaufen, der Punkt

$(2,3).$

Schritt 3: Schreiben Sie die Tangentengleichung

Es bleibt nur noch, die gefundenen Werte der Steigung und des Tangentenpunkts in seine Gleichung einzusetzen:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)$

Die Tangentengleichung lautet daher:

$\bm{y -3= 4(x-2)}$

Übung 2

Berechnen Sie die Gleichung der Tangente an die Kurve

$\displaystyle f(x)=-3x^2+2x$

am Koordinatenursprung.

Sehen Sie sich die Lösung an

Der Koordinatenursprung bezieht sich auf den Punkt

$(0,0).$

Wir müssen daher die Tangente an die Funktion im Punkt berechnen

$(0,0) .$

Zuerst bestimmen wir den Wert der Steigung der Tangente, indem wir die Ableitung im Koordinatenursprung berechnen:

$f(x)=-3x^2+2x \ \longrightarrow \ f'(x)= -6x+2$

$f'(0)= -6\cdot 0+2=2$

$m=f'(0)=2$

In diesem Fall kennen wir bereits einen Punkt, durch den die Tangente verläuft. Denn die Aussage sagt uns, dass die Gerade die Kurve im Koordinatenursprung, also im Punkt, tangieren muss

$(0,0).$

Der Punkt, den die Kurve und die Tangente gemeinsam haben, ist also der Punkt

$(0,0).$

Zum Schluss setzen Sie einfach die gefundenen Werte für die Steigung und den Tangentenpunkt in Ihre Gleichung ein:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)$

Zusammenfassend lautet die Tangentengleichung:

$y -0= 2(x-0)$

$\bm{y = 2x}$

Übung 3

Berechnen Sie die Tangente an die Kurve

$f(x)=x^2-2x-1$

was parallel zur rechten Seite ist

$y-4x-6=0$

Sehen Sie sich die Lösung an

In dieser Aufgabe wird uns gesagt, dass die Tangente parallel zur Geraden sein muss

$y-4x-6=0 .$

Und zwei Geraden sind parallel, wenn sie die gleiche Steigung haben. Die Tangente muss also die gleiche Steigung haben wie die Gerade

$y-4x-6=0.$

Das bedeutet, dass wir die Steigung der Geraden ermitteln müssen

$y-4x-6=0 .$

Dazu löschen wir die Variable und:

$y-4x-6=0 \ \longrightarrow \ y =4x+6$

Also die Steigung der Linie

$y=4x+5$

ist 4, da die Steigung einer Geraden die Zahl ist, die x multipliziert, wenn y klar ist.

Daher muss die Steigung der Tangente auch 4 sein, denn damit sie parallel sind, müssen sie die gleiche Steigung haben.

$m=4$

In diesem Fall sagen sie uns nicht den Tangentenpunkt zwischen der Kurve und der Tangente. Aber wir wissen, dass die Ableitung der Kurve am Tangentenpunkt gleich der Steigung der Tangente ist, d. h

$m=f'(x_0)$

. Nun, wie können wir den Wert kennen?

$m$

, können wir x ₀ aus der Gleichung ermitteln

$m=f'(x_0):$

Dazu berechnen wir zunächst die Ableitung von

$f(x):$

$f(x)= x^2-2x-1 \ \longrightarrow \ f'(x)=2x-2$

Und jetzt lösen wir es

$m=f'(x_0)$

wissend, dass

$m = 4 :$

$m =f'(x_0)$

$4 =2(x_0)-2$

$4+2 =2x_0$

$6 =2x_0$

$\cfrac{6}{2} =x_0$

$3=x_0$

Und sobald wir die x-Koordinate des Punktes kennen, können wir durch Berechnung die andere Koordinate des Punktes ermitteln

$f(3):$

$f(3)=3^2-2\cdot 3-1= 9-6-1=2$

Somit ist der Punkt, durch den sowohl die Kurve als auch die Tangente verlaufen, der Punkt

$(3,2).$

Es bleibt nur noch, die gefundenen Werte der Steigung und des Tangentenpunkts in seine Gleichung einzusetzen:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)$

Und die Tangentengleichung lautet:

$\bm{y -2=4(x-3)}$

Übung 4

Berechnen Sie die Tangente an die Kurve

$f(x)=2x^2+5x+1$

die mit der X-Achse einen Winkel von 45° bildet.

Sehen Sie sich die Lösung an

Die Problemstellung sagt uns, dass die Tangente mit der X-Achse einen Winkel von 45° bilden muss. In diesen Fällen muss die folgende Formel angewendet werden, um den Wert der Steigung zu ermitteln:

$m = \text{tg}\left(\alpha\right)$

$m = \text{tg}\left(45^{\text{o}}\right) = 1$

Die Anweisung gibt nicht den Tangentialpunkt zwischen der Kurve und der Tangente an. Aber wir wissen, dass die Ableitung der Kurve am Tangentenpunkt äquivalent zur Steigung der Tangente ist, d. h

$m=f'(x_0)$

. Wir können also x ₀ berechnen, indem wir die Gleichung lösen

$m=f'(x_0):$

Dazu berechnen wir zunächst die Ableitung von

$f(x):$

$f(x)=2x^2+5x+1\ \longrightarrow \ f'(x)=4x+5$