Punkt symmetrisch in bezug auf einen anderen punkt, eine linie und eine ebene

Hier erfahren Sie, wie Sie den Symmetriepunkt in Bezug auf einen anderen Punkt, in Bezug auf eine Linie und in Bezug auf eine Ebene berechnen. Darüber hinaus können Sie Beispiele und Übungen sehen, die Schritt für Schritt gelöst werden.

Punkt symmetrisch zu einem anderen Punkt

Bevor wir uns ansehen, wie der symmetrische Punkt berechnet wird, schauen wir uns an, was genau ein symmetrischer Punkt in Bezug auf einen anderen Punkt ist:

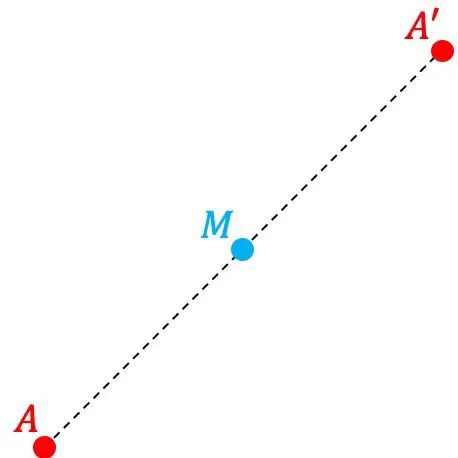
Punkt A‘ ist der symmetrische Punkt von Punkt A in Bezug auf einen anderen Punkt M, wenn Punkt A‘ symmetrisch im gleichen Abstand von Punkt M liegt wie der Abstand zwischen den Punkten A und M. Daher ist M der Mittelpunkt des Segments, das durch gebildet wird Punkte A und A‘.

Andererseits sagen wir auch, dass Punkt M das Symmetriezentrum ist.

Um die Koordinaten des Symmetriepunkts zu berechnen, verwenden wir die Formel für den Mittelpunkt eines Segments :

Aus dieser Gleichung extrahieren wir den unbekannten Punkt A‘ und erhalten die Formel für den Punkt, der symmetrisch zu einem anderen Punkt ist:

Beispiel für die Feststellung, dass der Punkt in Bezug auf einen anderen Punkt symmetrisch ist

Als Beispiel berechnen wir den Symmetriepunkt von Punkt A in Bezug auf Punkt M. Betrachten Sie die beiden Punkte:

Um den Symmetriepunkt zwischen diesen beiden Punkten zu bestimmen, wenden wir die Formel für den Symmetriepunkt in Bezug auf einen anderen an:

Jetzt ersetzen wir die Punkte in der Formel:

Und wir betreiben:

Punkt symmetrisch zu einer Geraden

Wir haben gerade die Vorstellung eines Punktes gesehen, der in Bezug auf einen anderen Punkt symmetrisch ist. Nun, die Symmetrie eines Punktes bezüglich einer Linie ist sehr ähnlich:

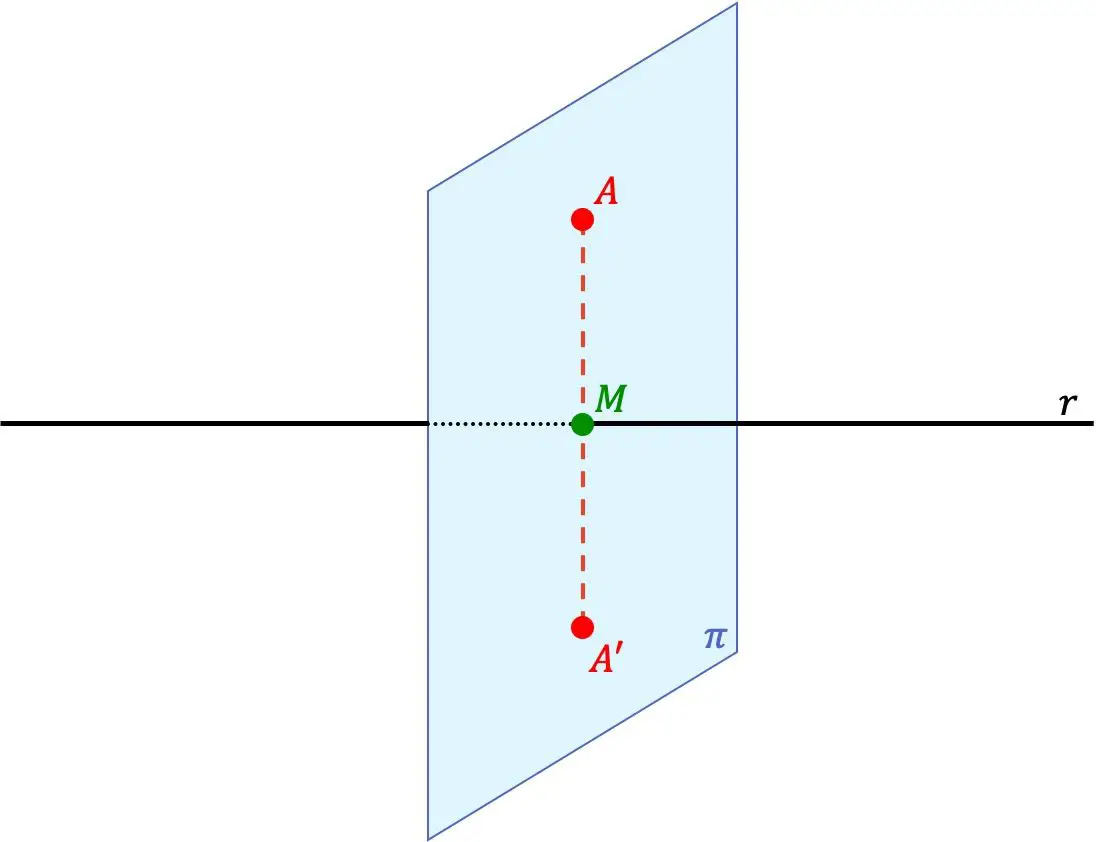
Punkt A‘ ist der symmetrische Punkt von Punkt A bezüglich einer Geraden, wenn die beiden Punkte A‘ und A auf derselben Geraden senkrecht zur Geraden liegen und außerdem der Abstand zwischen Punkt A‘ und der Geraden gleich dem Abstand ist zwischen Punkt A und der Linie.

Die Gerade r ist also auch eine Symmetrieachse zwischen den Punkten.

Um also den Symmetriepunkt des Punktes A in Bezug auf die Gerade r zu bestimmen, müssen wir das folgende Verfahren befolgen:

1. Wir finden die Ebene senkrecht zur Linie r , die durch Punkt A geht (Ebene π der vorherigen grafischen Darstellung). Dazu müssen wir den Richtungsvektor der Linie verwenden, der der Normalenvektor der Ebene ist.
2. Wir berechnen den Schnittpunkt zwischen der gefundenen Ebene und der Geraden (Punkt M im vorherigen Bild).
3. Wir verwenden die symmetrische Punkt-über-Punkt-Formel (siehe Abschnitt oben), um den symmetrischen Punkt von Punkt A in Bezug auf Punkt M zu finden. Das Ergebnis ist der symmetrische Punkt, nach dem wir gesucht haben.

Beispiel für die Berechnung des Symmetriepunkts bezüglich einer Geraden

Sobald wir wissen, wie man den Symmetriepunkt eines anderen Punktes in Bezug auf eine Linie berechnet, sehen wir eine beispielhaft gelöste Übung:

• Finden Sie den symmetrischen Punkt von Punkt A in Bezug auf die Linie r. Punkt und Linie gesagt:

Zuerst müssen wir die Ebene senkrecht zur Linie r berechnen, die durch den Punkt A verläuft. Der Normalvektor zu dieser Ebene ist der Richtungsvektor der Linie, dessen Komponenten die Terme vor dem Parameter sind

weil es in Form parametrischer Gleichungen ausgedrückt wird:

Und die Koeffizienten A, B und C der Gleichung einer Ebene stimmen mit den Koordinaten ihres Normalenvektors überein, daher:

Punkt A muss auf dieser Ebene liegen, daher können wir nun Punkt A in die Gleichung der Ebene einsetzen, um den Koeffizienten D zu ermitteln:

Damit lautet die Gleichung der Ebene senkrecht zur Linie ry, die durch Punkt A verläuft:

Sobald wir die Gleichung der Ebene kennen, müssen wir den Schnittpunkt der Ebene und der Geraden berechnen. Dazu setzen wir die Koordinaten der Geraden in die Gleichung der Ebene ein und lösen die resultierende Gleichung:

Jetzt ersetzen wir den Wert von

erhält man in der Gleichung der Geraden:

Der Schnittpunkt zwischen der Geraden r und der Ebene senkrecht dazu ist also:

Schließlich reicht es aus, den symmetrischen Punkt von Punkt A in Bezug auf Punkt M zu finden; Hierfür können wir die Formel am Anfang dieser Seite verwenden:

Punkt symmetrisch zu einer Ebene

Bevor wir uns mit der Methode zur Bestimmung des Symmetriepunkts eines anderen Punktes in Bezug auf eine Ebene befassen, sehen wir uns an, was seine Definition ist:

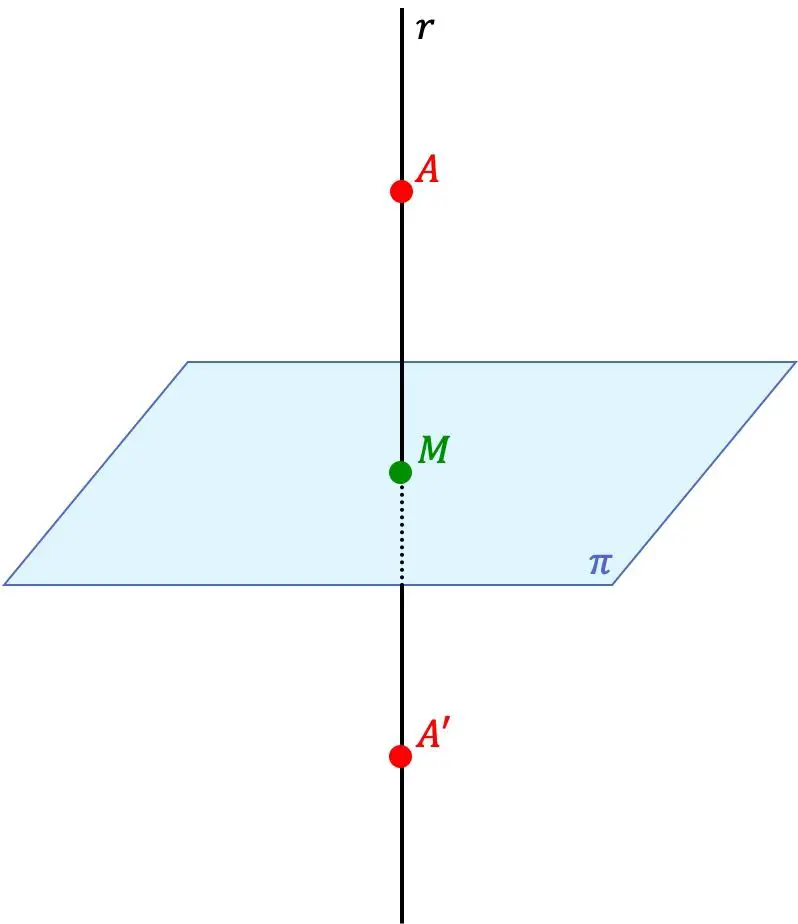
Punkt A‘ ist der symmetrische Punkt von Punkt A bezüglich einer Ebene, wenn die beiden Punkte A‘ und A auf derselben Geraden senkrecht zur Ebene liegen und außerdem der Abstand zwischen Punkt A‘ und der Ebene gleich dem Abstand ist zwischen Punkt A und der Ebene.

Die Ebene ist also auch eine Symmetrieebene zwischen den beiden Punkten.

Um die kartesischen Koordinaten des symmetrischen Punktes A in Bezug auf die Ebene π zu kennen, müssen Sie die folgenden Schritte ausführen:

1. Wir finden die Gleichung der Geraden senkrecht zur Ebene, die durch Punkt A verläuft. Dazu verwenden wir den Vektor normal zur Ebene als Richtungsvektor der Geraden.
2. Wir berechnen den Schnittpunkt zwischen der Ebene und der gefundenen Linie (Punkt M des vorherigen Bildes).
3. Wir verwenden die symmetrische Punkt-über-Punkt-Formel (siehe Anfangsabschnitt), um den symmetrischen Punkt von Punkt A in Bezug auf Punkt M zu finden. Das Ergebnis ist der symmetrische Punkt, nach dem wir gesucht haben.

Beispiel für die Bestimmung des Symmetriepunkts in Bezug auf eine Ebene

Unten sehen Sie ein gelöstes Problem bezüglich des Symmetriepunkts eines anderen Punktes in Bezug auf eine Ebene:

• Bestimmen Sie den Symmetriepunkt von A bezüglich der Ebene π. Nachdem ich Punkt und Plan gesagt habe:

Als Erstes müssen wir die Gleichung der Geraden finden, die senkrecht zur Ebene steht und durch den Punkt A verläuft. Dazu können wir den Vektor normal zur Ebene als Richtungsvektor der Geraden verwenden, dessen Komponenten X, Y, Z sind die Koeffizienten der Terme A, B bzw. C der Ebenengleichung:

Wir können nun die parametrischen Gleichungen der zur Ebene orthogonalen Geraden mit dem gefundenen Richtungsvektor und einem seiner Punkte (Punkt A) konstruieren:

Sobald wir die senkrechte Linie kennen, berechnen wir den Schnittpunkt der Ebene und der Linie, indem wir die Koordinaten der Linie in die Gleichung der Ebene einsetzen:

Jetzt ersetzen wir den Wert von

erhält man in der Gleichung der Geraden:

Der Schnittpunkt zwischen der Ebene und der Senkrechten ist also:

Schließlich müssen wir nur noch den symmetrischen Punkt von Punkt A in Bezug auf Punkt M finden. Dazu können wir die Formel am Anfang dieser Seite verwenden: