Vektor hinzufügen

Auf dieser Seite wird erklärt, wie man zwei Vektoren in der Ebene grafisch und numerisch addiert. Es gibt drei Möglichkeiten, sie grafisch hinzuzufügen: die Parallelogramm-, Kopf-an-Schwanz- und Polygon-Methode. Darüber hinaus finden Sie auch gelöste Übungen zur Vektoraddition und allen Eigenschaften der Vektoraddition.

Wie füge ich zwei Vektoren grafisch hinzu?

Grundsätzlich gibt es zwei Möglichkeiten, Vektoren aus ihrer Diagrammdarstellung hinzuzufügen. Mit beiden Formen wird das gleiche Ergebnis erzielt, einige bevorzugen jedoch die Addition mit der Kopf-Schwanz-Methode und andere mit der Parallelogramm-Methode . Wir erklären Ihnen daher die beiden Methoden, damit Sie die für Sie bevorzugte auswählen können. 😉

Andererseits werden diese beiden Methoden verwendet, um zwei Vektoren hinzuzufügen. Was passiert jedoch, wenn wir mehr als zwei Vektoren hinzufügen möchten? Es ist daher notwendig, die Polygonmethode zu verwenden, die darin besteht, nacheinander die Parallelogrammmethode anzuwenden. Die Erklärung finden Sie auch nach den Kopf-Schwanz- und Parallelogramm-Methoden.

Parallelogramm-Methode oder -Regel

Die Parallelogrammregel oder Parallelogrammmethode (oder Parallelogrammgesetz) ist ein grafisches Verfahren, mit dem Sie auf sehr einfache Weise die Summe zweier Vektoren ermitteln können. Um diesen Prozess anzuwenden, müssen folgende Schritte ausgeführt werden:

1. Zuerst zeichnen wir die Vektoren und positionieren sie am gleichen Anwendungspunkt, das heißt, wir platzieren die Ursprünge beider Vektoren am gleichen Punkt.
2. Dann zeichnen wir am Ende eines Vektors eine Linie parallel zum anderen Vektor. Und wir wiederholen den Schritt mit dem anderen Vektor. Wir erhalten also die Zeichnung eines Parallelogramms (daher der Name der Regel).
3. Das Ergebnis der Summe ist schließlich der Vektor, der vom gemeinsamen Ursprung bis zum Schnittpunkt der beiden parallelen Linien verläuft.

Schauen Sie sich das folgende allgemeine Beispiel an, in dem zwei Vektoren mit der Parallelogrammregel addiert werden:

Das Ergebnis der Summe der Vektoren ist die Diagonale des Parallelogramms, das sie mit ihren Parallelen bilden.

Kopf-Schwanz-Methode

Die Kopf-Schwanz-Methode , oder auch Dreiecksmethode genannt, ist ein weiteres Verfahren, mit dem zwei Vektoren grafisch addiert werden können. In diesem Fall sind folgende Schritte zu befolgen:

1. Verschieben Sie einen hinzugefügten Vektor und platzieren Sie ihn so, dass sein Ursprung direkt am Ende des anderen hinzugefügten Vektors liegt.
2. Das Ergebnis der Vektoraddition ist das Segment, das vom Anfang des ersten hinzugefügten Vektors bis zum Ende des anderen Vektors reicht. Wenn Sie genau hinschauen, wird ein Dreieck mit den beiden hinzugefügten Vektoren und dem hinzugefügten Vektor vervollständigt.

Hier ist ein Beispiel für die Vektoraddition mit der Kopf-an-Schwanz-Methode:

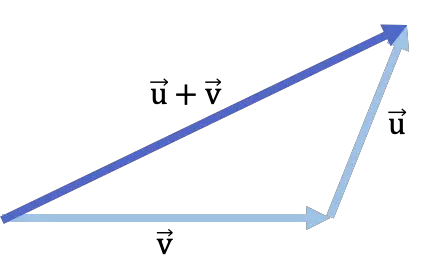
Polygonmethode

Nachdem wir gesehen haben, wie man die Summe zweier Vektoren grafisch löst, werden wir sehen, wie das geht, wenn wir mehr als zwei Vektoren haben.

Wenn Sie drei oder mehr Vektoren hinzufügen möchten, gibt es eine Technik, um die Berechnung der Operation zu beschleunigen. Diese Technik wird als Polygonmethode bezeichnet und besteht aus der sukzessiven Anwendung der Kopf-an-Schwanz-Methode:

1. Wir müssen zunächst jeden Vektor nach dem anderen platzieren, sodass der Ursprung eines Vektors mit dem Ende eines anderen Vektors zusammenfällt. Die Reihenfolge, in der wir sie platzieren, ist unerheblich.
2. Und das Ergebnis der Summe ist der Vektor, den man erhält, indem man den Anfang des ersten Vektors mit dem Ende des letzten Vektors verbindet.

Schauen Sie sich das folgende Beispiel an, in dem 4 Vektoren hinzugefügt werden:

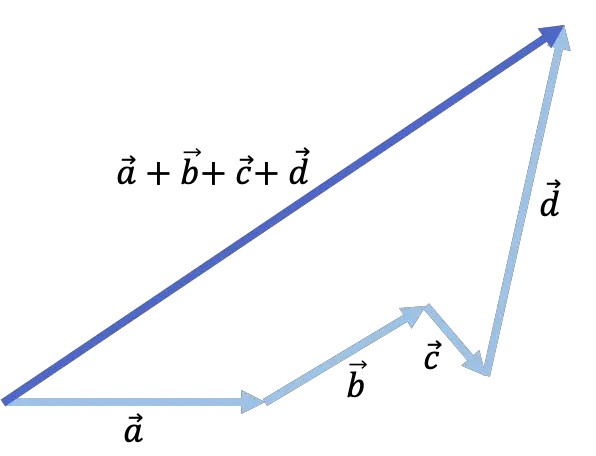
Berechnen Sie die Summe zweier Vektoren numerisch

Sobald wir wissen, wie man Vektoren geometrisch addiert, werden wir sehen, wie man eine Vektorsumme numerisch oder algebraisch berechnet.

Zum Beispiel die Summe zwischen Vektoren

Und

Ost:

Andererseits müssen wir bedenken, dass die Vektoraddition zweier Vektoren nicht dasselbe ist wie die Addition der Module der Vektoren, sondern dass die Ergebnisse völlig unterschiedlich sind. Sie können die Unterschiede zwischen den beiden Operationen an den Eigenschaften der Vektorgröße (auch Vektorgröße genannt) erkennen.

Vektoreigenschaften hinzufügen

Die Vektoraddition hat die folgenden Eigenschaften:

• Assoziative Eigenschaft : Das Setzen von Klammern zwischen der Summe mehrerer Vektoren verändert das Ergebnis der Operation nicht.

• Kommutative Eigenschaft – Im Gegensatz zur Vektorsubtraktion ist das Ergebnis der Addition zwischen zwei Vektoren unabhängig von der Reihenfolge, in der sie addiert werden.

• Eigenschaft des Gegenelements : Die Summe eines Vektors plus seinem Gegenteil, also seiner Negation, ist gleich 0.

• Eigenschaft des neutralen Elements : Offensichtlich ist jeder Vektor plus Null oder Nullvektor äquivalent zum Vektor selbst:

Vektoradditionsprobleme gelöst

Übung 1

Berechnen Sie die Summe der Vektoren grafisch

Und

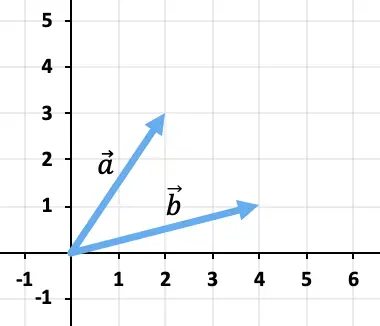
Um die beiden Vektoren zu addieren, verwenden wir die Kopf- und Schwanzregel. Wir werden daher den Ursprung des Vektors platzieren

am Ende des Vektors

, und die Summe ist der Vektor, der vom Ursprung der Koordinaten bis zum Ende reicht

Daher ist das Ergebnis der Vektoraddition:

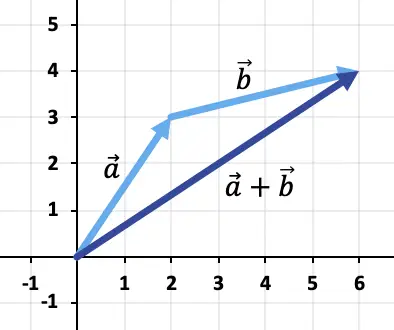
Übung 2

Lösen Sie die Summe der Vektoren grafisch

Und

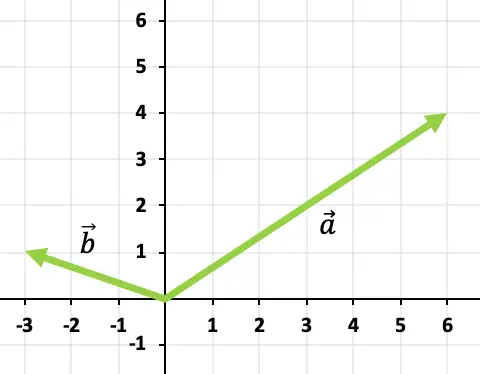
Um die beiden Vektoren zu addieren, verwenden wir die Kopf-Schwanz-Regel. Wir werden daher den Ursprung des Vektors lokalisieren

am Ende des Vektors

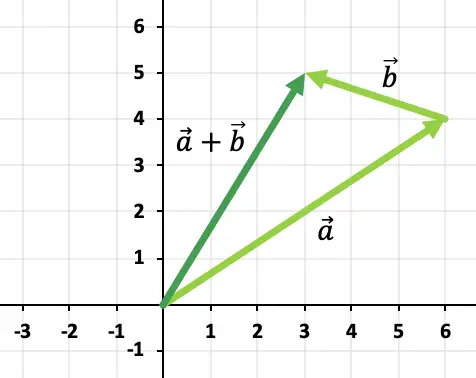
, und der Summenvektor ist derjenige, der vom Ursprung der Achsen bis zum Ende reicht

Daher ist das Ergebnis der Vektoraddition:

Übung 3

Bestimmen Sie grafisch den Vektor, der sich aus der Addition aller im Diagramm dargestellten Vektoren ergibt:

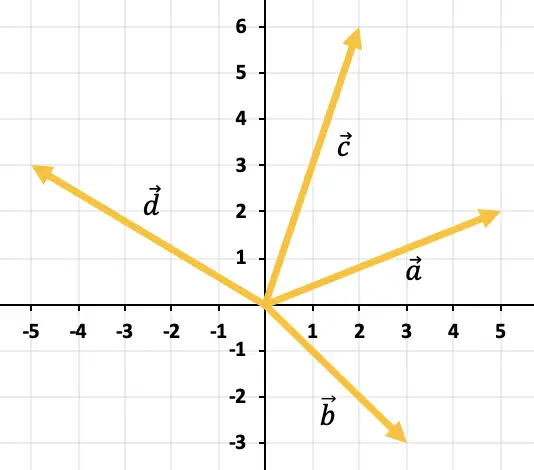
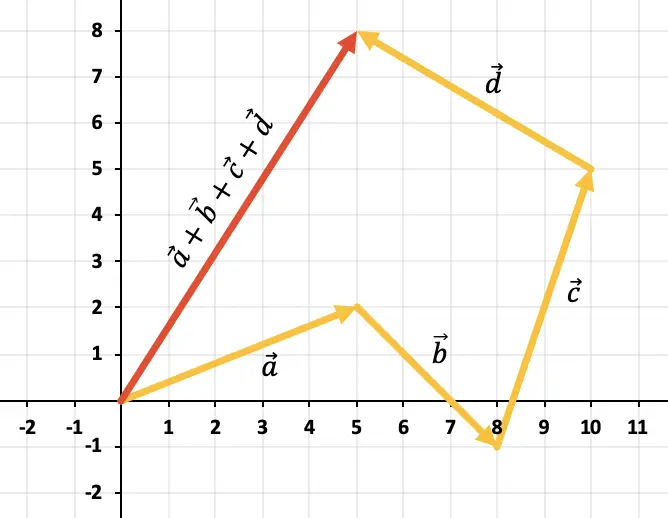
Um mehr als zwei Vektoren aus dem Diagramm hinzuzufügen, müssen Sie die Polygonregel verwenden. Wir müssen also die Vektoren so verschieben, dass sie stetig bleiben, also nacheinander (die Reihenfolge ist irrelevant). Die Summe aller Vektoren ist also der Vektor, der vom Ursprung des ersten Vektors bis zum Ende des letzten Vektors reicht.

Das Ergebnis der Summe der 4 Vektoren ist also der rot dargestellte Vektor:

Übung 4

Ermitteln Sie numerisch die Summe der folgenden Vektoren:

Um zwei Vektoren numerisch zu addieren, müssen Sie ihre jeweiligen Koordinaten addieren:

Übung 5

Berechnen Sie analytisch die Summe der folgenden Vektoren:

Um Vektoren numerisch zu addieren, müssen Sie ihre jeweiligen Koordinaten hinzufügen: