Auf dieser Seite finden Sie die Erklärung, wie die Addition von Polynomen erfolgt. Darüber hinaus können Sie Beispiele für Polynomsummen und sogar Schritt für Schritt gelöste Aufgaben sehen. Abschließend erklären wir auch, welche Eigenschaften diese Art von Operation mit Polynomen hat.
Wie addiere ich Polynome?
Um in der Mathematik zwei oder mehr Polynome zu addieren, müssen die Terme der ähnlichen Polynome addiert werden. Das heißt, beim Addieren von Polynomen werden Terme addiert, die den gleichen Literalteil haben (gleiche Variablen und gleiche Exponenten).
Somit kann eine Summe von Polynomen auf zwei verschiedene Arten erfolgen: mit der vertikalen Methode oder mit der horizontalen Methode. Nachfolgend finden Sie eine Erläuterung beider Verfahren. Wir empfehlen Ihnen jedoch, zunächst zu lernen, wie Sie Polynome vertikal addieren, und dann mit der horizontalen Methode fortzufahren. Bleiben Sie natürlich bei der Variante, die Sie bevorzugen.
Vertikale Polynome hinzufügen
Als nächstes sehen wir uns anhand eines Beispiels an, wie zwei Polynome vertikal addiert werden:
- Fügen Sie die folgenden zwei Polynome hinzu:
![]()
![]()
Als erstes müssen wir ein Polynom unter ein anderes legen, sodass die gleichen Terme der beiden Polynome spaltenweise ausgerichtet sind:
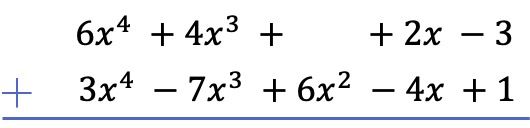
Achtung: Wenn ein Polynom keinen Term eines bestimmten Grades hat, muss das Feld leer bleiben. Zum Beispiel
![]()
Sie haben kein Monom vom Grad 2, weshalb auf Ihrer Website ein leerer Bereich vorhanden ist.
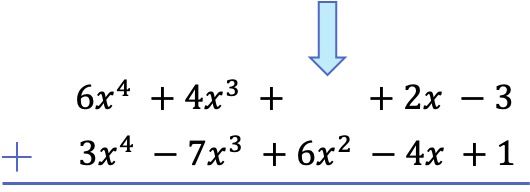
Nachdem wir alle Terme vom höchsten zum niedrigsten Grad geordnet haben, addieren wir die Koeffizienten in jeder Spalte, wobei die Literalteile gleich bleiben:
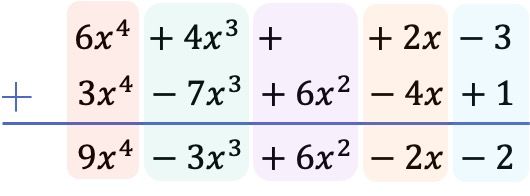
Folglich ergibt sich aus der Summe der beiden Polynome folgendes Ergebnis:
![]()
Nachdem Sie nun die Addition von Polynomen verstanden haben, wissen Sie, dass Sie auch Brüche addieren können, die aus Polynomen bestehen. Diese Art von Operation wird algebraische Bruchaddition genannt. Klicken Sie auf diesen Link und erfahren Sie nicht nur, wie die Summen algebraischer Brüche berechnet werden, sondern auch, wie alle Operationen mit algebraischen Brüchen gelöst werden.
Horizontale Addition von Polynomen
Wir haben gerade gesehen, wie man Polynome vertikal addiert, aber jetzt schauen wir uns die andere Methode zum Addieren von Polynomen an: das horizontale Addieren von Polynomen. Sicherlich ist dieses Verfahren schneller als das vorherige, es ist jedoch erforderlich, die Konzepte der Polynome besser zu beherrschen.
Sehen wir uns also anhand eines Beispiels an, woraus diese Methode zum Addieren von Polynomen besteht. Und damit Sie die Unterschiede zwischen den beiden Methoden sehen können, fügen wir die gleichen Polynome wie im vorherigen Beispiel hinzu:
- Berechnen Sie die Summe der folgenden zwei Polynome:
![]()
![]()
Sie müssen zunächst die beiden Polynome in der gleichen Operation positionieren, also nacheinander:
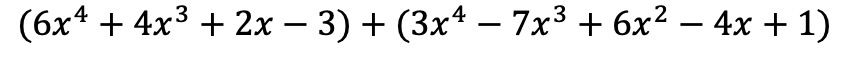
Und nun fügen wir die Terme hinzu, die identische Literalteile haben, also die Terme mit denselben Variablen (Buchstaben) und denselben Exponenten. Nicht ähnliche Begriffe können nicht hinzugefügt werden.
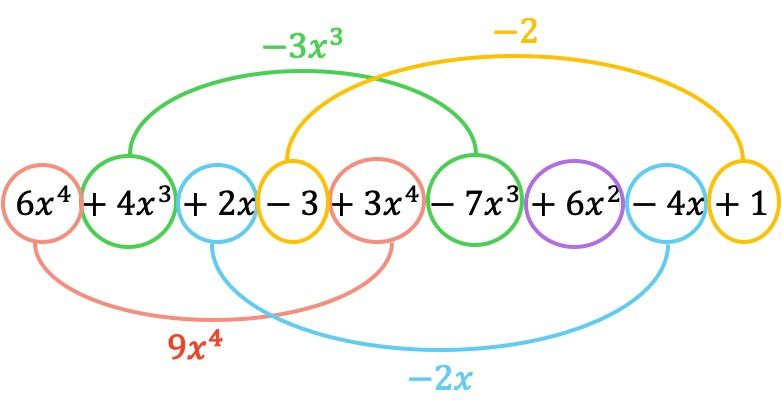
Das aus der Addition resultierende Polynom ist daher:

Wie Sie sehen, haben wir mit beiden Methoden das gleiche Ergebnis erzielt, sodass Sie beim Addieren von Polynomen die für Sie am besten geeignete Methode verwenden können.
Probleme beim Addieren von Polynomen gelöst
Damit Sie üben können, hinterlassen wir Ihnen einige gelöste Aufgaben zu Summen von Polynomen. Wenn Sie Fragen haben, können Sie diese in den Kommentaren auf der Seite stellen und wir werden sie so schnell wie möglich beantworten.
Übung 1
Fügen Sie die folgenden zwei Polynome hinzu:
![]()
![]()
In diesem Fall addieren wir die beiden Polynome vertikal. Dazu ordnen wir die Polynome nach Grad und addieren die in derselben Spalte stehenden Monome:
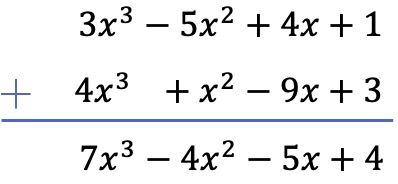
Übung 2
Lösen Sie die Summe der folgenden zwei Polynome:
![]()
![]()
Wir werden die beiden Polynome mit der vertikalen Methode summieren. Daher ordnen wir die Polynome nach Grad und fügen die Terme hinzu, die in derselben Spalte stehen:
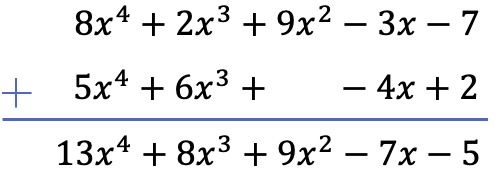
Beachten Sie, dass in diesem speziellen Fall ein Leerzeichen in der Spalte 2. Grades des zweiten Polynoms gelassen werden muss, da es keinen quadratischen Term hat.
Übung 3
Was ist die Summe der folgenden zwei Polynome?
![]()
![]()
Wir werden die Addition der beiden Polynome mit der vertikalen Methode durchführen. ALSO:
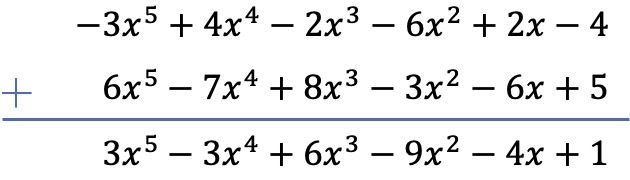
Übung 4
Berechnen Sie die Summe der folgenden drei Polynome:
![]()
![]()
![]()
Wir berechnen die Summe der 3 Polynome mit der vertikalen Methode. Wir ordnen daher die Polynome nach Graden an und fügen die Terme hinzu, die sich in derselben Spalte befinden:
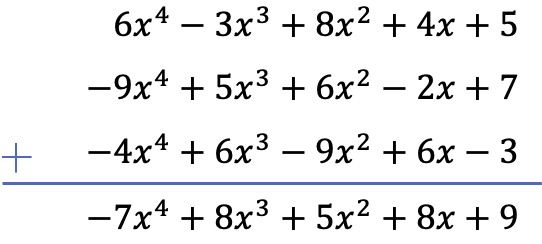
👉👉👉Da Sie nun gesehen haben, wie sich zwei Polynome addieren, könnte Sie eine weitere charakteristische Operation von Polynomen interessieren: der gemeinsame Faktor. Das Extrahieren eines gemeinsamen Faktors aus einem Polynom ist ziemlich kompliziert (und schwer zu verstehen), tatsächlich werden dabei viele Fehler gemacht. Aus diesem Grund haben wir einen Leitfaden erstellt, in dem wir Ihnen Schritt für Schritt erklären, wie Sie den gemeinsamen Faktor extrahieren , damit Sie ihn perfekt verstehen und bei dieser Operation keine Fehler machen. Erfahren Sie, welche Tipps es zum Extrahieren des gemeinsamen Faktors aus einem Polynom gibt, indem Sie auf den Link klicken.
Eigenschaften der Addition von Polynomen
Die Summe der Polynome weist folgende Eigenschaften auf:
- Assoziative Eigenschaft : Beim Addieren von 3 oder mehr Polynomen spielt es keine Rolle, wie die Polynome gruppiert sind, da das Ergebnis immer das gleiche ist. Das heißt, die folgende Gleichheit wird überprüft:
![]()
- Kommutative Eigenschaft : Bei der Addition von Polynomen verändert die Reihenfolge der Additionen das Ergebnis der Addition nicht.
![]()
- Neutrales Element : Offensichtlich entspricht die Addition eines Polynoms plus einem anderen Polynom mit einem numerischen Wert von Null dem ersten Polynom.
![]()
- Gegenstück : Das Ergebnis der Addition eines beliebigen Polynoms plus seinem Gegenpolynom ist immer Null.
![]()
Was halten Sie von der Erklärung? Fanden Sie das hilfreich? Welche Methode zum Addieren von Polynomen bevorzugen Sie, vertikal oder horizontal? Wir haben Sie in den Kommentaren gelesen! 👀