Auf dieser Seite erklären wir, wie man Polynome subtrahiert. Darüber hinaus finden Sie mehrere Beispiele und gelöste Schritt-für-Schritt-Übungen zum Subtrahieren von Polynomen.
Wie subtrahiere ich Polynome?
Um zwei Polynome zu subtrahieren, müssen Sie die Terme der ähnlichen Polynome subtrahieren. Mit anderen Worten: Beim Subtrahieren von Polynomen werden Terme subtrahiert, die denselben Literalteil haben (gleiche Variablen und gleiche Exponenten).
In der Mathematik kann man die Subtraktion von Polynomen auf zwei verschiedene Arten berechnen: mit der vertikalen Methode oder mit der horizontalen Methode. Nachfolgend finden Sie eine Erläuterung beider Verfahren. Wir empfehlen Ihnen jedoch, zunächst zu lernen, wie man Polynome vertikal subtrahiert, und dann mit der horizontalen Methode fortzufahren. Bleiben Sie natürlich bei der Variante, die Sie bevorzugen.
Subtraktion vertikaler Polynome
Als nächstes sehen wir uns anhand eines Beispiels an, wie zwei Polynome vertikal subtrahiert werden:
- Führe die Subtraktion durch
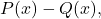
sind die beiden Polynome:
![]()
![]()
Das erste, was wir tun müssen, um eine Polynomsubtraktion zu finden, besteht darin, ein Polynom unter das andere zu legen, sodass die gleichen Terme der beiden Polynome in Spalten ausgerichtet sind:
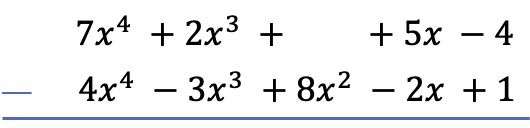
Achtung: Wenn ein Polynom keinen Term eines bestimmten Grades hat, muss das Feld leer bleiben. Zum Beispiel das Polynom
![]()
hat kein quadratisches Monom, daher gibt es an seiner Stelle einen leeren Raum.
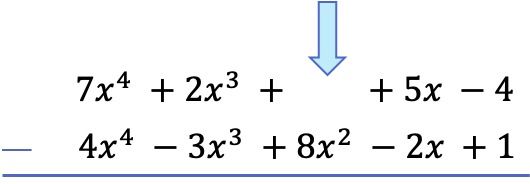
Obwohl wir jetzt Polynome direkt subtrahieren können, ist es ziemlich leicht, das Vorzeichen zu verwechseln, wenn wir es auf diese Weise tun. Um Polynome zu subtrahieren, ist es daher am besten , das Vorzeichen aller Terme im Subtraktionspolynom (dem Subtraktionspolynom) zu ändern und dann die Addition durchzuführen. Denn das Subtrahieren eines Polynoms ist dasselbe wie das Addieren seines entgegengesetzten Polynoms.
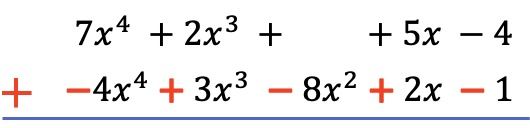
Und nachdem wir alle Terme vom höchsten zum niedrigsten Grad geordnet und die Terme des Polynoms unten negiert haben, addieren wir die Koeffizienten jeder Spalte, wobei die Literalteile gleich bleiben:
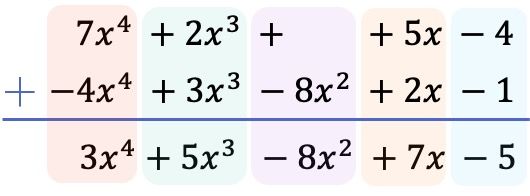
Daher ergibt sich aus der Subtraktion der beiden Polynome folgendes Ergebnis:
![]()
Falls Ihnen der letzte Schritt nicht klar ist, überlasse ich Ihnen die Erklärung, wie dieAddition von Polynomen durchgeführt wird. Tatsächlich ist es wichtig, dass Sie die Addition von Polynomen beherrschen, um Polynome erfolgreich subtrahieren zu können. Auf der verlinkten Seite finden Sie auch Beispiele und gelöste Aufgaben zum Addieren von Polynomen und können darüber hinaus die Unterschiede zwischen Addieren und Subtrahieren von Polynomen sehen.
Subtraktion horizontaler Polynome
Wir haben gerade gesehen, wie man Polynome vertikal subtrahiert, aber jetzt sehen wir uns die andere Methode an, die es zum Subtrahieren von Polynomen gibt: Polynome horizontal subtrahieren. Dieses Verfahren ist sicherlich schneller als das vorherige, es ist jedoch eine bessere Beherrschung der Konzepte von Polynomen erforderlich.
Sehen wir uns also anhand eines Beispiels an, woraus diese Methode zum Subtrahieren von Polynomen besteht. Und damit Sie die Unterschiede zwischen den beiden Methoden sehen können, subtrahieren wir dieselben Polynome wie im vorherigen Beispiel:
- Berechnen Sie den Rest
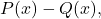
sind die beiden Polynome:
![]()
![]()
Wir müssen die beiden Polynome zunächst in Form einer algebraischen Operation, also nacheinander, umsetzen:
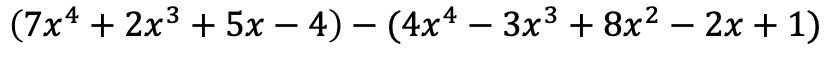
Die Monome in der ersten Klammer bleiben gleich, die Terme in der zweiten Klammer müssen jedoch das Vorzeichen ändern, da ihnen ein Negativ vorangestellt ist:
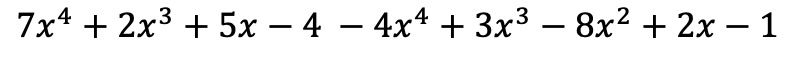
Und jetzt gruppieren wir Begriffe, die identische Literalteile haben, also Begriffe mit denselben Variablen (Buchstaben) und Exponenten. Begriffe, die nicht ähnlich sind, können nicht addiert oder subtrahiert werden.
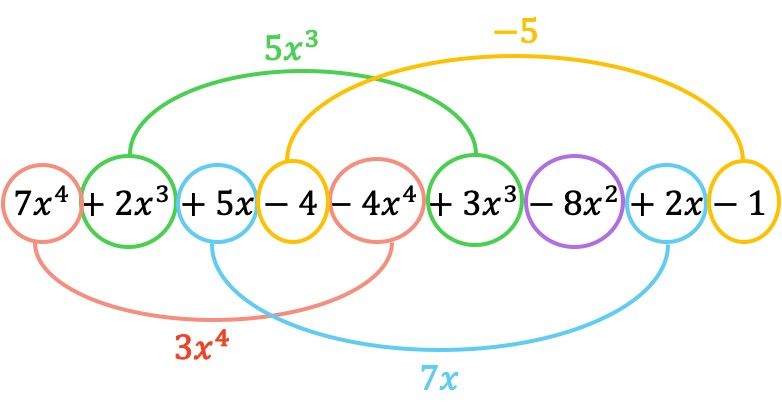
Das aus der Subtraktion resultierende Polynom ist also:
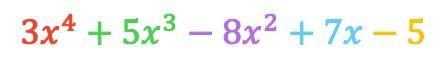
Wie Sie sehen, haben wir mit beiden Methoden das gleiche Ergebnis erzielt, sodass Sie die für Sie am besten geeignete Methode verwenden können.
Nachdem Sie nun die beiden Methoden zur Lösung der Polynomsubtraktion kennengelernt haben, wussten Sie, dass Sie auch Brüche mit Polynomen subtrahieren können? Und nicht nur Subtraktionen, sondern alle Arten von Operationen. Erfahren Sie, wie Operationen mit algebraischen Brüchen durchgeführt werden, indem Sie auf diesen Link klicken.
Probleme beim Subtrahieren von Polynomen gelöst
Damit Sie üben können, überlassen wir Ihnen einige gelöste Polynomsubtraktionsübungen. Wenn Sie Fragen zu einer Übung haben, können Sie diese in den Kommentaren auf der Seite stellen. Wir werden diese so schnell wie möglich beantworten.
Übung 1
Subtrahiere das Polynom
![]()
minus dem Polynom
![]()
![]()
![]()
In diesem Fall subtrahieren wir die beiden Polynome vertikal. Dazu ordnen wir die Polynome zunächst nach Grad, ändern dann das Vorzeichen der übrigen Polynomterme und fügen schließlich die in derselben Spalte stehenden Monome hinzu:
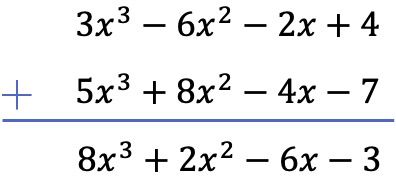
Übung 2
Lösen Sie das Subtraktionspolynom
![]()
minus dem Polynom
![]()
![]()
![]()
Das Subtrahieren zweier Polynome läuft darauf hinaus, das Gegenteil des subtrahierten Polynoms zum Diminutivpolynom zu addieren. Daher ändern wir das Vorzeichen der Terme des Unterauftragspolynoms (das verbleibende) und fügen die Polynome hinzu:
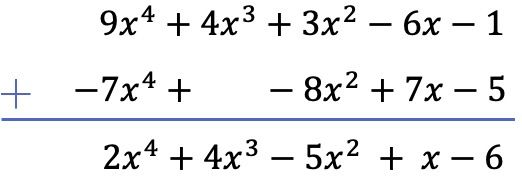
Beachten Sie, dass in diesem speziellen Fall ein Leerraum in der Spalte 3. Grades des zweiten Polynoms gelassen werden muss, da es keinen Term dritten Grades hat.
Übung 3
Finden Sie das Ergebnis der Subtraktion des Polynoms
![]()
minus dem Polynom
![]()
![]()
![]()
In diesem Fall lösen wir die Subtraktion der beiden Polynome vertikal. Zuerst ordnen wir die Polynome vom größten zum kleinsten Grad, ändern dann das Vorzeichen der Terme des verbleibenden Polynoms und fügen schließlich die gleichen Terme hinzu:
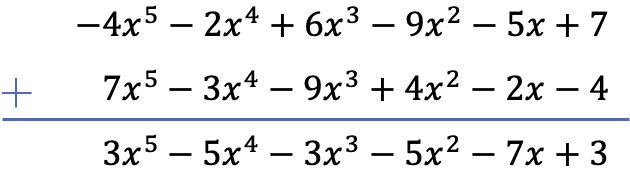
Übung 4
Berechnen Sie die folgende Operation mit Polynomen:
![]()
![]()
![]()
![]()
In diesem Fall sind 3 Polynome an der Operation beteiligt, davon 2 Subtraktionen. Um die Operation zu lösen, ändern wir daher das Vorzeichen aller Terme der beiden verbleibenden Polynome und addieren dann die Polynome.
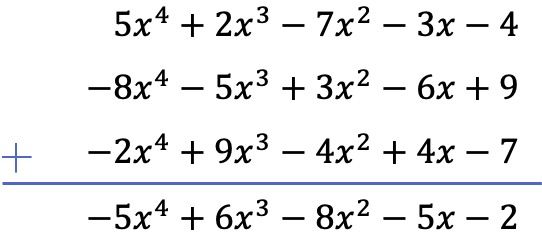
Was halten Sie von der Erklärung? Fanden Sie es nützlich? Welche Methode zum Subtrahieren von Polynomen bevorzugen Sie, vertikal oder horizontal? Wir haben Sie in den Kommentaren gelesen! 👀