In diesem Artikel erklären wir, was stetige Funktionen sind und wie man ermittelt, ob eine Funktion an einem Punkt stetig ist oder nicht. Darüber hinaus finden Sie Eigenschaften stetiger Funktionen und Kontinuitätsanalysen der häufigsten Funktionen. Abschließend können Sie mit gelösten Übungen zur kontinuierlichen Funktion üben, um das Konzept vollständig zu verstehen.
Was ist eine stetige Funktion?
Die Stetigkeit einer Funktion kann grafisch untersucht werden. Eine stetige Funktion ist eine Funktion, die in einem Diagramm dargestellt werden kann, ohne den Bleistift vom Papier zu nehmen.
Kontinuierliche Funktion
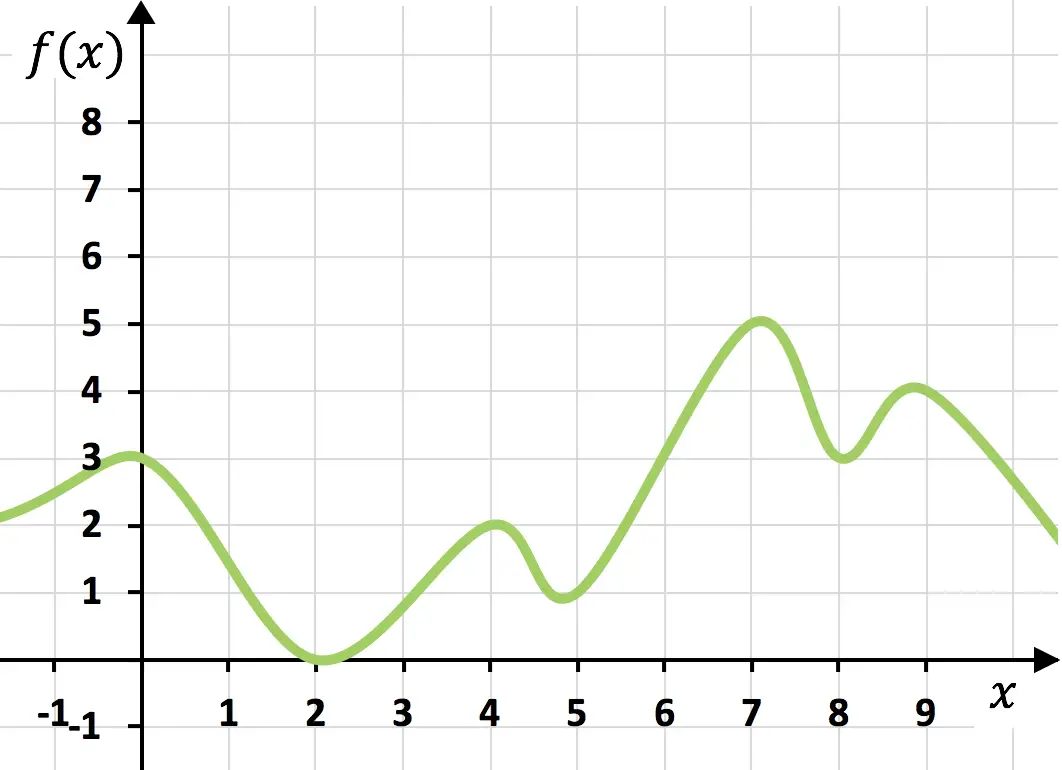
Die obige Funktion ist kontinuierlich, da sie in einem Strich gezeichnet werden kann, ohne die Hand vom Papier zu nehmen.
Wenn andererseits die vorherige Kontinuitätsbedingung nicht in eine Funktion eingefügt wird, spricht man von einer diskontinuierlichen Funktion .
Diskontinuierliche Funktion
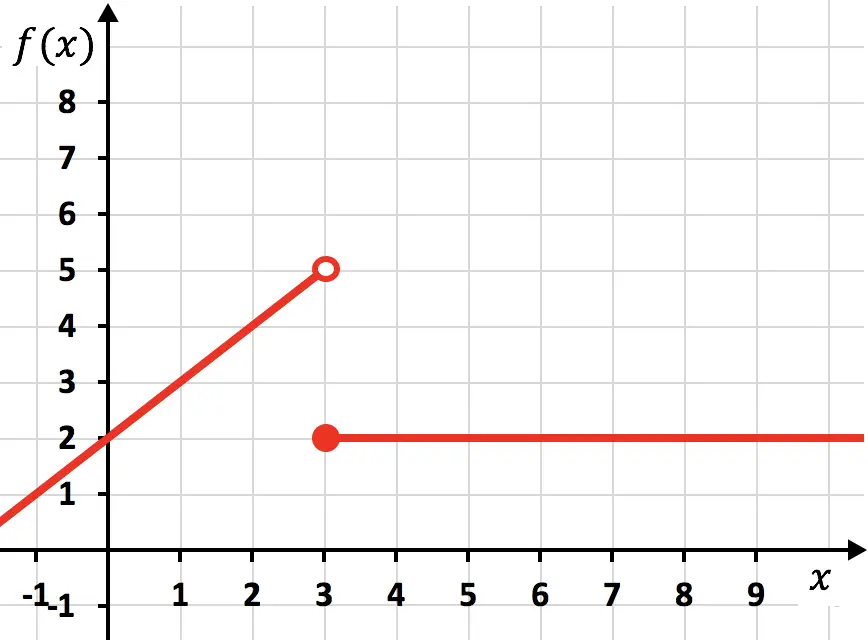
Die vorherige Funktion ist diskontinuierlich, da Sie zu ihrer Darstellung zwei Linien mit dem Bleistift zeichnen müssen. In diesem Fall hört die Funktion bei x=3 auf, stetig zu sein, wir sagen daher, dass x=3 ein Unstetigkeitspunkt ist.
Darüber hinaus gibt es drei Arten von Diskontinuitäten : vermeidbare Diskontinuität, unvermeidliche Diskontinuität mit endlichem Sprung und unvermeidliche Diskontinuität mit unendlichem Sprung. Unter dem folgenden Link können Sie sehen, wie die einzelnen Arten von Diskontinuitäten aussehen und was sie jeweils unterscheidet:
➤ Siehe: Arten von Diskontinuitäten
Stetigkeit einer Funktion an einem Punkt
Sobald wir sehen, wie der Graph einer stetigen Funktion aussieht, schauen wir uns an, wie wir analytisch feststellen können, ob eine Funktion stetig ist oder nicht.
Mathematisch gesehen ist eine Funktion an einem Punkt stetig, wenn die folgenden drei Bedingungen erfüllt sind:
- Die Funktion existiert an diesem Punkt, das heißt, das Bild des Punktes existiert.
- An diesem Punkt liegt die Grenze der Funktion. Daher sind die linken und rechten seitlichen Grenzen der Funktion an diesem Punkt gleich.
- Das Bild des Punktes stimmt mit dem Grenzwert der Funktion an diesem Punkt überein.
![]()
![]()
![]()
Wenn also die drei Kontinuitätsbedingungen an allen Punkten einer Funktion erfüllt sind, ist die Funktion stetig.
Als Beispiel analysieren wir die Stetigkeit der folgenden stückweisen Funktion:
Auch wenn Sie Abschnitte wechseln, an der Stelle
![]()
Die Funktion ist stetig, da die seitlichen Grenzen der Funktion an diesem Punkt gleich sind und eher mit dem Wert der Funktion an diesem Punkt übereinstimmen.
![]()
Andererseits ist die Funktion im Punkt nicht stetig
![]()
weil die beiden seitlichen Grenzen unterschiedlich sind und daher der Grenzwert der Funktion an dieser Stelle nicht existiert:
![]()
Kurz gesagt, die durch die Stücke definierte Funktion ist in allen reellen Zahlen außer in stetig
![]()
wo es eine Diskontinuität gibt.
Wir können auch überprüfen, dass die Funktion in unstetig ist
![]()
denn um es grafisch darzustellen, ist es an dieser Stelle notwendig, den Bleistift vom Papier zu entfernen.
Kontinuität elementarer Funktionen
Bestimmte Arten von Funktionen sind aufgrund ihrer Eigenschaften kontinuierlich:
- Konstante Funktionen sind in allen reellen Zahlen stetig.
![]()
- Polynomfunktionen sind für alle reellen Zahlen stetig.
![]()
- Rationale (oder gebrochene) Funktionen sind in allen reellen Zahlen stetig, außer in Werten, die den Nenner des Bruchs aufheben; an diesen Punkten weist die Funktion eine Diskontinuität auf.
![]()
- Exponentialfunktionen sind über alle reellen Zahlen stetig:
![]()
- Logarithmische Funktionen sind an allen Stellen stetig, an denen ihr Argument positiv ist.
![]()
- Die Stetigkeit irrationaler Funktionen oder Funktionen mit Wurzeln hängt vom Index des Radikals (n) ab. Wenn der Index gerade ist, handelt es sich um stetige Funktionen an allen Punkten, deren Wurzelargument gleich oder größer Null ist. Wenn der Index jedoch ungerade ist, handelt es sich um stetige Funktionen für alle reellen Zahlen.
![]()
- Die Stetigkeit trigonometrischer Funktionen hängt von der Art der Funktion ab. Die Sinusfunktion und die Kosinusfunktion sind über die Menge der reellen Zahlen stetig, die Tangensfunktion ist jedoch an den Punkten unstetig
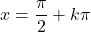
(wobei k eine ganze Zahl ist).
![]()
Eigenschaften stetiger Funktionen
Sean
![]()
Und
![]()
zwei stetige Funktionen am Punkt
![]()
Nächste:
- Die Summe zweier stetiger Funktionen an einem Punkt ist eine weitere stetige Funktion an diesem Punkt.
![]()
- Das Produkt zweier stetiger Funktionen an einem Punkt ist gleich einer anderen stetigen Funktion an diesem Punkt.
![]()
- Die Division zweier stetiger Funktionen an einem Punkt führt zu einer weiteren stetigen Funktion an diesem Punkt, solange dieser Punkt die Divisionsfunktion nicht aufhebt.
![]()
- Die Zusammensetzung zweier stetiger Funktionen an einem Punkt führt zu einer stetigen Funktion an diesem Punkt.
![]()
➤ Siehe: Was ist eine zusammengesetzte Funktion?
Gelöste Übungen zur Stetigkeit einer Funktion
Übung 1
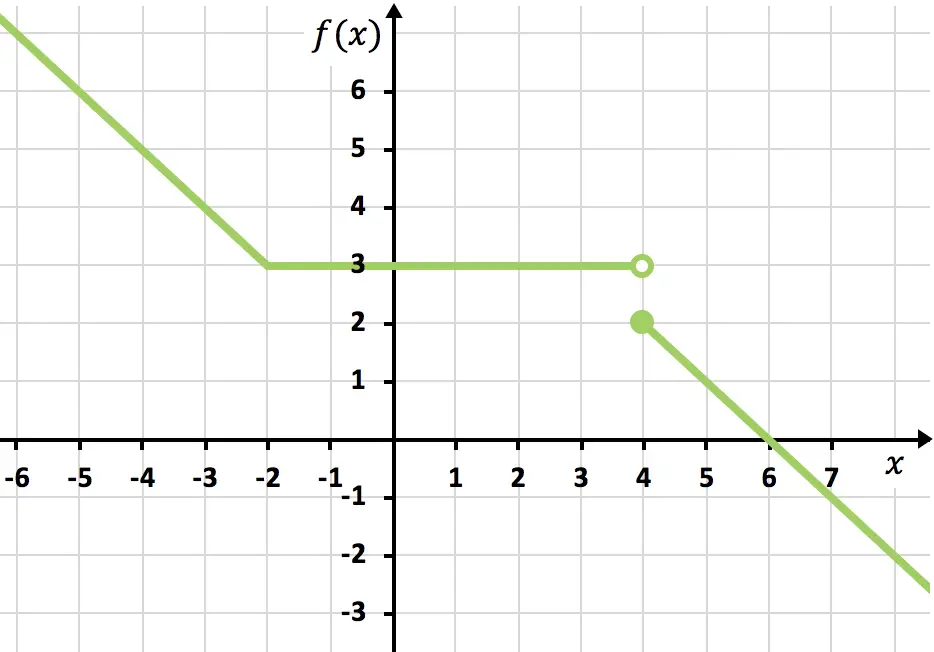
Finden Sie die Diskontinuitäten der in der folgenden Grafik gezeigten Funktion. Bestimmen Sie außerdem, um welche Art von Diskontinuität es sich handelt.
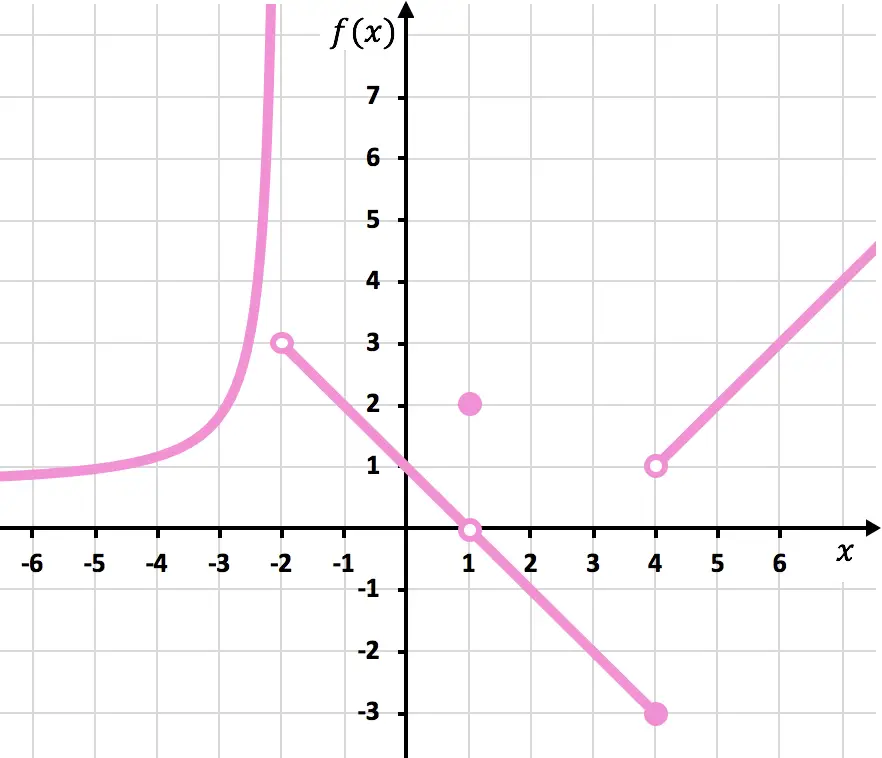
Hinweis: Um diese Übung durchzuführen, empfehlen wir Ihnen, sich zunächst mit den verschiedenen Arten von Diskontinuitäten zu befassen und wie sie identifiziert werden. Die Erklärung finden Sie im Link zum Prinzip der Diskontinuitätstypen .
Um die Funktion zu zeichnen, müssen Sie den Bleistift bei x=-2, bei x=1 und bei x=4 anheben. Die Funktion ist daher an diesen drei Punkten unstetig.
Bei x=-2 beträgt die linke Grenze +∞ und die rechte Grenze 3. Da also eine der Seitengrenzen unendlich ist, weist die Funktion bei x=-2 unvermeidlich eine unendliche Sprungdiskontinuität auf.
![]()
Der Grenzwert der Funktion bei x=1 ist 0 und andererseits ist der Wert der Funktion bei x=1 gleich 2. Die Funktion weist daher bei x=1 eine vermeidbare Diskontinuität auf.
![]()
![]()
Bei x = 4 beträgt der linke Grenzwert -3 und der rechte Grenzwert 1. Da die beiden seitlichen Grenzwerte unterschiedlich sind und keiner von ihnen Unendlichkeit ergibt, weist die Funktion bei x = 4 zwangsläufig eine endliche Sprungunstetigkeit auf.
![]()
Übung 2
Bestimmen Sie die Punkte, an denen die im folgenden Diagramm gezeigte Funktion unstetig ist.
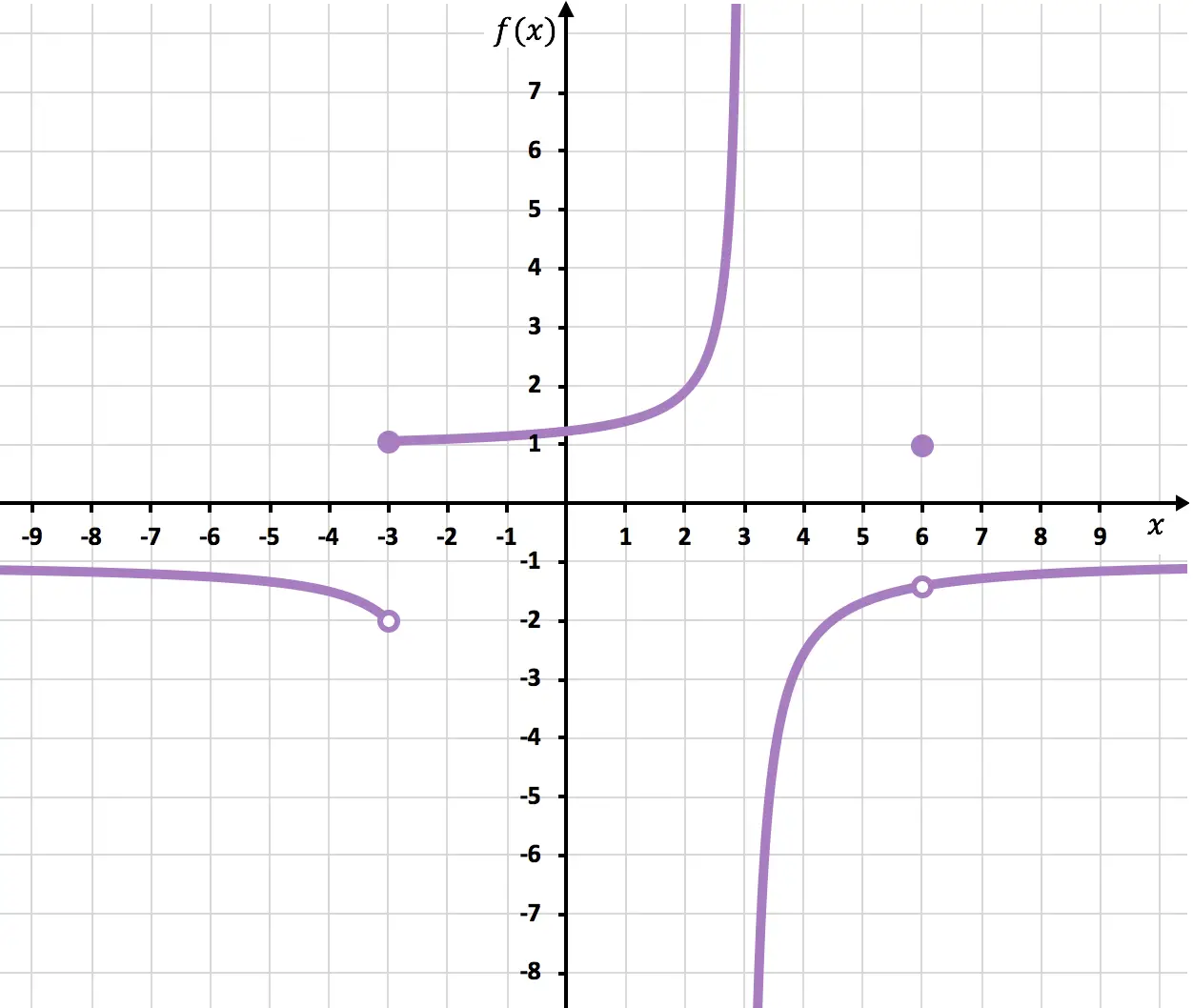
Am Punkt x=6 wird die Funktion unterbrochen, da es einen offenen Punkt gibt. Wenn x sich 6 nähert, liegt die Grenze bei -1,4, aber f(6)=1. Die Funktion weist daher bei x=6 eine vermeidbare Diskontinuität auf, da der Wert des Grenzwerts nicht mit dem Wert der Funktion übereinstimmt:
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4](https://mathority.org/wp-content/ql-cache/quicklatex.com-33612be383c71fea04c8c886710f7f10_l3.png)
![]()
Bei x=-3 fallen die seitlichen Grenzen nicht zusammen und keine ergibt Unendlich. Die Funktion weist daher unvermeidlich eine endliche Sprungunstetigkeit bei x=-3 auf.
![]()
Und schließlich weist die Funktion bei x = 3 zwangsläufig eine Sprungunstetigkeit ins Unendliche auf, da mindestens eine seitliche Grenze an dieser Stelle zur Unendlichkeit führt.
![]()
Übung 3
Analysieren Sie die Stetigkeit der folgenden rationalen Funktion:
![]()
Rationale Funktionen sind in ihrem gesamten Definitionsbereich stetig, also in allen reellen Zahlen mit Ausnahme der Werte, die den Nenner aufheben. Daher setzen wir den Nenner der rationalen Funktion gleich Null, um zu sehen, welche Punkte nicht zum Definitionsbereich gehören:
![]()
![]()
![]()
Die Funktion ist daher an allen Punkten außer x=5 stetig.
Übung 4
Analysieren Sie die Stetigkeit der folgenden stückweisen Funktion:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a18e6289d268e6ea9fe1ee3ea14d31fd_l3.png)
Auch im ersten Abschnitt ist die Funktion stetig,
![]()
, wie im zweiten Abschnitt,
![]()
, da es sich um Polynomfunktionen handelt.
Der einzige Punkt, an dem die Funktion unstetig sein könnte, ist also der Punkt, an dem die Funktion stückweise bricht. Berechnen wir also an dieser Stelle die seitlichen Grenzen:
![]()
![]()
Die beiden seitlichen Grenzen fallen also zusammen, der Grenzwert der Funktion, wenn x gegen 1 tendiert, ist gleich 3:
![]()
Darüber hinaus ist das Bild von x=1 auch 3:
![]()
Da also der Grenzwert der Funktion bei x=1 gleich dem Bild dieses Punktes ist, ist die Funktion bei Punkt x=1 stetig. Und deshalb ist sie in allen reellen Zahlen stetig.
![]()
Übung 5
Untersuchen Sie die Kontinuität der folgenden irrationalen Funktion:
![]()
Es handelt sich um eine Wurzelfunktion mit geradem Index, daher ist die Funktion stetig, solange das Argument der Wurzel größer als 0 ist (da die Quadratwurzel einer negativen Zahl nicht existiert):
![]()
Wir lösen die Ungleichung:
![]()
![]()
![]()
Die Lösung besteht aus allen Zahlen größer oder gleich -3. Die Funktion ist daher auf dem Intervall ihres Definitionsbereichs stetig:
![]()
Übung 6
Analysieren Sie die Stetigkeit der folgenden logarithmischen Funktion:
![]()
Dies ist eine logarithmische Funktion, und es gibt weder den Logarithmus einer negativen Zahl noch den Logarithmus von 0. Daher existiert die Funktion, solange das Argument des Logarithmus positiv (größer als Null) ist:
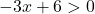 Wir lösen die Ungleichung:
Wir lösen die Ungleichung:
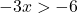
![]()
Denken Sie daran, dass Sie das Vorzeichen der Ungleichung umkehren müssen, wenn Sie eine negative Zahl durch die andere Seite einer Ungleichung dividieren.
![]()
Die Lösung besteht aus allen Zahlen kleiner als 2. Der Definitionsbereich der Funktion ist daher:
![]()
Die Funktion ist daher an jedem Punkt ihres Definitionsbereichs stetig.
Übung 7
Berechnen Sie die Stetigkeit der folgenden Funktion:
![]()
Im Nenner des Bruchs haben wir eine Wurzel mit einem geraden Index, sodass die Funktion immer dann existiert, wenn der Inhalt der Wurzel gleich oder größer als Null ist:
![]()
Aber auch die Wurzel liegt im Nenner des Bruchs, und der Nenner eines Bruchs kann niemals 0 sein. Die Funktion existiert also nur, wenn der Inhalt der Wurzel strikt größer als 0 ist:
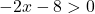 Nun lösen wir die Ungleichung:
Nun lösen wir die Ungleichung:
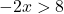
![]()
Denken Sie daran, dass wir, wenn wir die Seiten einer negativen Zahl durch Multiplikation oder Division einer Ungleichung ändern, auch das Ungleichheitszeichen drehen müssen.
![]()
Das Ergebnis sind alle Zahlen kleiner als -4. Somit werden der Bereich der Funktion und damit ihre Stetigkeit durch das folgende Intervall definiert:
![]()
Übung 8
Berechnen Sie den Wert von k , sodass die Funktion durchgehend stetig ist
![]()
![\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.“ title=“Rendered by QuickLaTeX.com“ height=“65″ width=“225″ style=“vertical-align: 0px;“></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-f7d8f0d6e0730c139c3baff0989a8fe7_l3.png)