Auf dieser Seite finden Sie die detaillierteste Erklärung der Steigung einer Linie: Wie lautet ihre Formel, Berechnungsbeispiele, was das Konzept der Steigung einer Linie bedeutet usw. Außerdem erfahren Sie, wie Sie die Steigung leicht identifizieren können einer Geraden aus ihrer Gleichung und können zusätzlich mit Schritt für Schritt gelösten Übungen üben.
Formel für die Steigung einer Geraden
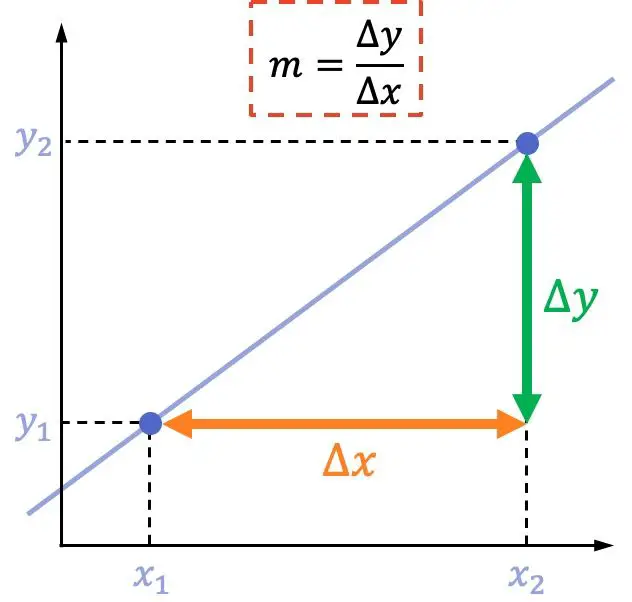
Die Steigung einer Geraden ist gleich der vertikalen Verschiebung zwischen zwei Punkten dividiert durch die horizontale Verschiebung zwischen diesen beiden Punkten.
Das heißt, es sind zwei Punkte auf einer Geraden gegeben:
![]()
Die Formel für die Steigung einer Geraden lautet:
![]()
Beispiel für die Berechnung der Steigung einer Geraden aus zwei Punkten
Als nächstes sehen wir ein Beispiel dafür, wie die Steigung einer Geraden mit der Formel berechnet wird:
- Berechnen Sie die Steigung der Geraden, die durch die folgenden zwei Punkte verläuft:
![]()
Um die Steigung dieser Geraden zu ermitteln, wenden Sie einfach ihre Formel an:
![]()
Die Steigung der Geraden beträgt daher 3.
Ermitteln der Steigung einer Geraden aus ihrer Gleichung
Im obigen Abschnitt haben wir gerade gesehen, wie man die Steigung einer Geraden numerisch bestimmt. Es ist jedoch nicht immer notwendig, Berechnungen durchzuführen, sondern der Wert kann auch aus der Gleichung einer Geraden ermittelt werden. Jeder Gleichungstyp ist anders, daher werden wir jeden Fall separat analysieren.
Steigung bei gegebener expliziter Gleichung der Geraden
Die explizite Gleichung der Geraden folgt dem folgenden Ausdruck:
![]()
Dann der Parameter
![]()
entspricht der Steigung der Geraden.
Steigung gegeben durch die Punkt-Steigungsgleichung der Geraden
Die Formel für die Punkt-Steigungsgleichung der Geraden lautet wie folgt:
![]()
Nach wie vor der Koeffizient
![]()
entspricht der Steigung der Geraden.
Steigung bei gegebener impliziter Gleichung der Geraden
Gegeben sei die implizite Gleichung der Geraden (auch allgemeine oder kartesische Gleichung genannt):
![]()
Die Steigung der Geraden kann wie folgt ermittelt werden:
![]()
Steigung unter Berücksichtigung des Richtungsvektors der Geraden
Der Richtungsvektor der Linie ist der Vektor, der ihre Richtung angibt. Wenn also der Richtungsvektor einer Geraden ist:
![]()
Die Steigung dieser Geraden beträgt:
![]()
Steigung bei gegebenem Winkel
Schließlich bildet eine Linie einen Winkel
![]()
im positiven Teil der Abszissenachse (X-Achse) entspricht seine Steigung dem Tangens des Winkels:
![]()
Bedeutung der Steigung einer Geraden
Mit all den oben genannten Informationen wissen wir bereits genau, wie man die Steigung einer Geraden ermittelt. Aber wirklich … was bedeutet die Steigung einer Linie?
Die Steigung einer Linie gibt die vertikalen Einheiten an, um die die Linie für jede horizontale Einheit des Diagramms ansteigt.
In der Darstellung der folgenden Linie können Sie beispielsweise sehen, dass sie für jede horizontale Einheit um 2 vertikale Einheiten vorrückt, da ihre Steigung gleich 2 ist.

Darüber hinaus gibt die Steigung einer Linie auch deren Steilheit an:
- Wenn eine Linie zunimmt (steigt), ist ihre Steigung positiv.
- Wenn eine Linie abnimmt (absteigend), ist ihre Steigung negativ.
- Wenn eine Linie vollständig horizontal ist, ist ihre Steigung gleich 0.
- Wenn eine Linie vollständig vertikal ist, ist ihre Steigung gleich unendlich.


Relative Position der Linien
Andererseits kann die relative Lage zwischen zwei Geraden auch aus den Eigenschaften der Steigungen ermittelt werden:
- Wenn zwei Geraden unterschiedliche Steigungen haben, bedeutet das, dass sie sich schneiden , das heißt, sie schneiden sich in einem Punkt.
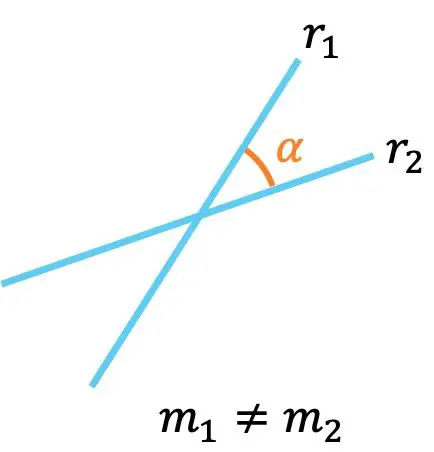
Zusätzlich kann der Winkel zwischen den beiden Geraden über ihre Steigungen mit der folgenden Formel berechnet werden:
![]()
- Zweitens: Wenn zwei Geraden die gleiche Steigung haben, bedeutet dies, dass sie parallel sind.

- Schließlich erfüllen die Steigungen zweier senkrechter oder orthogonaler Linien (die 90° bilden) die folgende Bedingung:

Dies ist eine Möglichkeit herauszufinden, ob zwei Linien parallel oder senkrecht zueinander sind. Es gibt jedoch auch andere Methoden, von denen einige sogar noch schneller sind. Weitere Informationen finden Sie in der Erklärung der Rechtwinkligkeit und Parallelität zwischen Geraden . Darüber hinaus wird auf diesen Seiten auch erklärt, wie man eine Linie senkrecht (oder parallel) zu einer anderen findet.
Probleme der Steigung einer Linie gelöst
Übung 1
Ermitteln Sie die Steigung der Geraden, die durch die folgenden zwei Punkte verläuft:
![]()
Um die Steigung der Linie zu berechnen, müssen Sie die Formel verwenden:
![]()
Übung 2
Berechnen Sie die Steigung der Geraden, die durch die folgenden zwei Punkte verläuft:
![]()
Um die Steigung der Linie zu ermitteln, müssen Sie die Formel verwenden:
![]()
Übung 3
Wie groß ist die Steigung jeder Geraden?
![Rendered by QuickLaTeX.com \begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d405c8176957af59906c98149714570_l3.png)
A) Die Gerade wird als implizite Gleichung ausgedrückt, ihre Steigung beträgt also 2 (der Term, der mit der Gleichung einhergeht).
![]()
).
B) Die Gerade wird durch ihre Punkt-Steigungsgleichung definiert, ihre Steigung beträgt also 4 (die Zahl vor den Klammern).
C) Die Gerade hat die Form einer impliziten Gleichung, daher ist ihre Steigung:
![]()
D) Die Gerade ist in Form parametrischer Gleichungen definiert, daher müssen wir zunächst ihren Richtungsvektor finden und damit die Steigung der Geraden berechnen. Somit sind die Komponenten des Richtungsvektors die Terme, die den Koeffizienten begleiten
![]()
![]()
Und sobald wir den Richtungsvektor der Geraden kennen, können wir die Steigung der Geraden bestimmen:
![]()
Übung 4
Bestimmen Sie die Steigung jeder graphischen Linie:

blau rechts
Die blaue Linie erhöht sich für jedes X um ein Y, sodass ihre Steigung gleich 1 ist.
![]()
rechts grün
Die grüne Linie erhöht sich für jedes X um drei Y, sodass ihre Steigung 3 beträgt .
![]()
rote Linie
Die rote Linie nimmt für jedes X um zwei Y ab, sodass ihre Steigung gleich -2 ist .
![]()