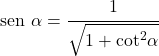Auf dieser Seite finden Sie alles über die Sinusfunktion: Was ist sie, wie lautet ihre Formel, wie stellt man sie in einem Diagramm dar, die Eigenschaften dieser Art von Funktion, Amplitude, Periode usw. Darüber hinaus können Sie verschiedene Beispiele für Sinusfunktionen sehen, um das Konzept vollständig zu verstehen. Er erklärt sogar den Sinussatz und die Beziehungen, die die Sinusfunktion zu anderen trigonometrischen Verhältnissen hat.
Sinusfunktionsformel
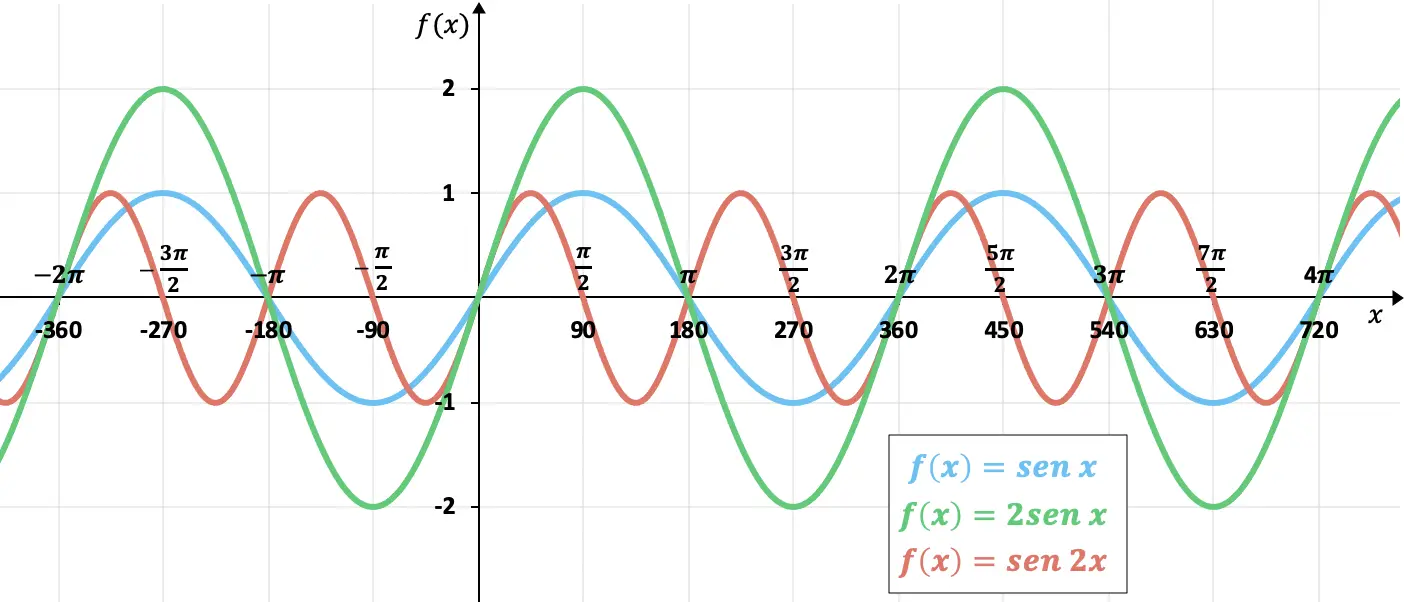
Die Sinusfunktion eines Winkels α ist eine trigonometrische Funktion, deren Formel als das Verhältnis zwischen dem gegenüberliegenden Schenkel und der Hypotenuse eines rechtwinkligen Dreiecks (Dreieck mit rechtem Winkel) definiert ist.

Diese Art mathematischer Funktionen wird oft mit der Abkürzung „Sünde“ oder „Sünde“ (von lat. sinus ) geschrieben. Darüber hinaus kann es auch als Sinus-, Sinus- oder Sinusfunktion bezeichnet werden.
Die Sinusfunktion ist neben dem Kosinus und dem Tangens eines Winkels eines der bekanntesten trigonometrischen Verhältnisse.
Charakteristische Werte der Sinusfunktion
Einige Winkel wiederholen sich häufig und daher ist es praktisch, den Wert der Sinusfunktion bei diesen Winkeln zu kennen:
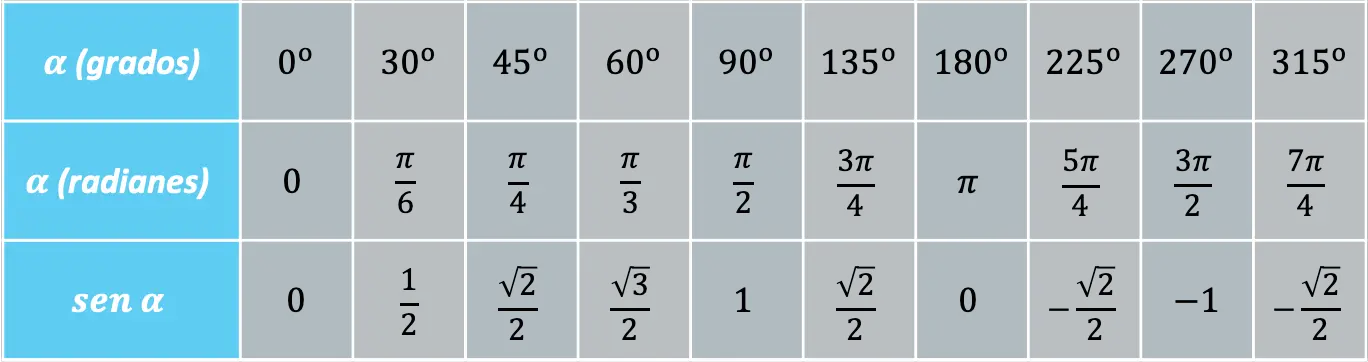
Das Vorzeichen der Sinusfunktion hängt also davon ab, in welchem Quadranten sich der Winkel befindet: Liegt der Winkel im ersten oder zweiten Quadranten, ist der Sinus positiv, liegt der Winkel hingegen im dritten oder vierten Quadranten , der Sinus wird negativ sein.
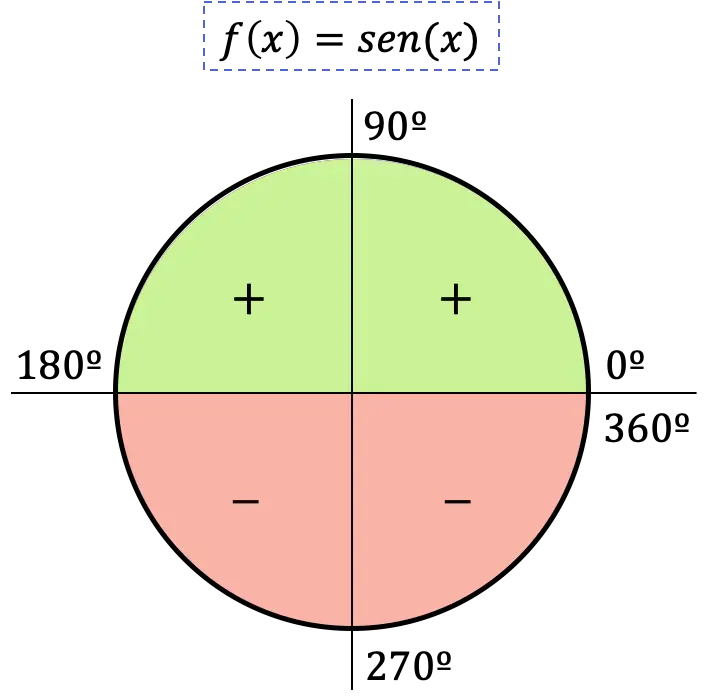
Grafische Darstellung der Sinusfunktion
Mit der Wertetabelle, die wir im vorherigen Abschnitt gesehen haben, können wir die Sinusfunktion grafisch darstellen. Wenn wir also die Sinusfunktion grafisch darstellen, erhalten wir:
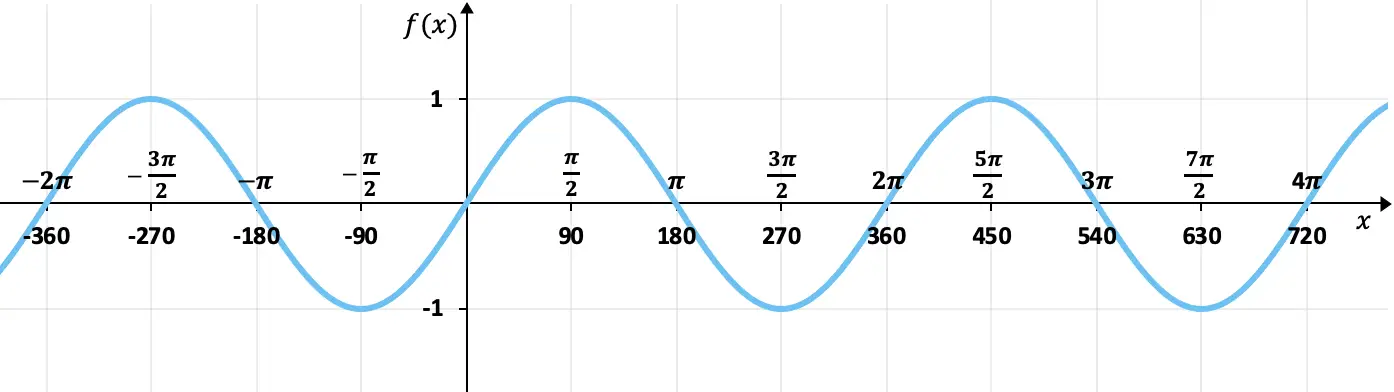
Wie Sie der Grafik entnehmen können, liegen die Werte der Bilder der Sinusfunktion immer zwischen +1 und -1, das heißt, sie wird oben durch +1 und unten durch -1 begrenzt. Darüber hinaus wiederholen sich die Werte alle 360 Grad (2π Bogenmaß), es handelt sich also um eine periodische Funktion mit einer Periode von 360°.
Andererseits erkennen wir in diesem Diagramm vollkommen, dass die Sinusfunktion ungerade ist, weil ihre entgegengesetzten Elemente entgegengesetzte Bilder haben, oder mit anderen Worten, sie ist symmetrisch in Bezug auf den Ursprung (0,0). Beispielsweise ist der Sinus von 90° 1 und der Sinus von -90° ist -1.
Eigenschaften der Sinusfunktion
Die Sinusfunktion hat folgende Eigenschaften:
- Der Definitionsbereich der Sinusfunktion sind alle reellen Zahlen, da die Funktion, wie die Grafik zeigt, für jeden Wert der unabhängigen Variablen x existiert.
![]()
- Der Pfad oder Bereich der Sinusfunktion reicht von minus 1 bis plus 1 (beide einschließlich).
![]()
- Es handelt sich um eine stetige und ungerade Funktion mit der Periodizität 2π.
![]()
- Diese Art von trigonometrischer Funktion hat einen einzigen Schnittpunkt mit der y-Achse (Y-Achse) im Punkt (0,0).
![]()
- Stattdessen schneidet es periodisch die Abszisse (X-Achse) an mehreren Koordinaten von Pi.
![]()
- Das Maximum der Sinusfunktion tritt auf, wenn:
![]()
- Und umgekehrt liegt das Minimum der Sinusfunktion bei:
![]()
- Die Ableitung der Sinusfunktion ist der Kosinus:
![]()
- Schließlich ist das Integral der Sinusfunktion das geänderte Vorzeichen des Cosinus:
![]()
Periode und Amplitude der Sinusfunktion
Wie wir in seinem Diagramm gesehen haben, ist die Sinusfunktion eine periodische Funktion, das heißt, ihre Werte wiederholen sich entsprechend einer Frequenz. Darüber hinaus hängen die Maximal- und Minimalwerte, zwischen denen es schwankt, von seiner Amplitude ab. Daher sind zwei Merkmale, die die Sinusfunktion bestimmen, ihre Periode und ihre Amplitude:
![]()
- Die Periode der Sinusfunktion ist der Abstand zwischen zwei Punkten, an denen sich der Graph wiederholt, und wird mit der folgenden Formel berechnet:
![]()
- Die Amplitude der Sinusfunktion entspricht dem Koeffizienten vor dem Sinusterm.
![]()
Unten sehen Sie eine Grafik, die die Auswirkungen einer Änderung der Periode oder Amplitude zeigt:

In der grün dargestellten Funktion können wir sehen, dass die Funktion durch die Verdoppelung der Amplitude von +2 auf -2 geht, statt von +1 auf -1. Andererseits sieht man in der rot dargestellten Funktion, dass sie doppelt so schnell abläuft wie die „kanonische“ Sinusfunktion, da ihre Periode halbiert wurde.
Sinussatz
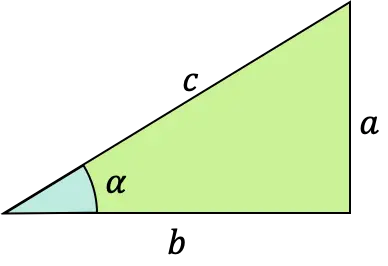
Obwohl der Sinus normalerweise auf rechtwinklige Dreiecke angewendet wird, gibt es auch einen Satz, der für jede Art von Dreieck gilt: den Sinussatz.
Das Sinusgesetz verknüpft die Seiten und Winkel jedes Dreiecks wie folgt:
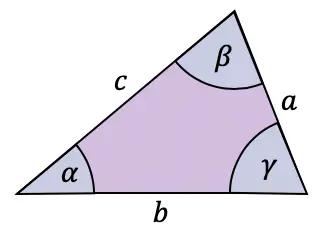
![]()
Beziehungen der Sinusfunktion zu anderen trigonometrischen Verhältnissen
Nachfolgend finden Sie die Sinusbeziehungen mit den wichtigsten trigonometrischen Verhältnissen in der Trigonometrie.
Kosinusverhältnis
- Der Graph der Kosinusfunktion entspricht der Sinuskurve, ist jedoch verschoben
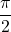
nach links, sodass die beiden Funktionen durch den folgenden Ausdruck verknüpft werden können:
![]()
- Sie können Sinus und Cosinus auch mit der trigonometrischen Grundidentität in Beziehung setzen:
![]()
Beziehung zur Tangente
- Obwohl der Beweis komplex ist, kann der Sinus nur durch den Tangens ausgedrückt werden:
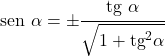
Beziehung zum Kosekans
- Sinus und Kosekans sind multiplikative Umkehrungen:
![]()
Beziehung zur Sekante
- Der Sinus kann gelöscht werden, sodass er nur noch von der Sekante abhängt:
![]()
Zusammenhang mit dem Kotangens
- Sinus und Kotangens eines Winkels hängen durch die folgende Gleichung zusammen: