Auf dieser Seite erfahren Sie, was senkrechte Ebenen sind, wie Sie feststellen können, ob zwei Ebenen senkrecht zueinander stehen, wie Sie eine senkrechte Ebene berechnen, Beispiele und gelöste Übungen zu senkrechten Ebenen, …
Was sind zwei senkrechte Ebenen?
In der analytischen Geometrie sind zwei Ebenen senkrecht, wenn sie sich im rechten Winkel (90°) schneiden.
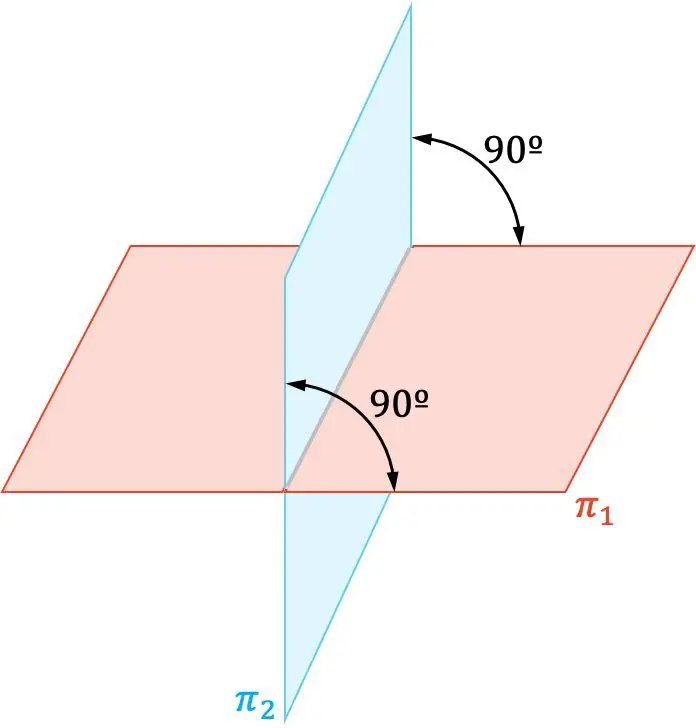
Darüber hinaus sind auch die Normalenvektoren zweier senkrechter Ebenen orthogonal zueinander.
Offensichtlich ist der Abstand zwischen zwei senkrechten Ebenen immer Null, da sie sich in einer Geraden schneiden. Obwohl es sehr einfach erscheint, ist das Konzept des Abstands zwischen zwei Ebenen sehr wichtig. Wir empfehlen Ihnen daher, den Link zu besuchen, wenn Sie Fragen dazu haben.
Andererseits sind zwei senkrecht zueinander stehende Ebenen nicht die einzig mögliche relative Position zwischen Ebenen, da sich zwei Ebenen im Raum (in R3) auch schneiden, parallel oder zusammenfallen können.
Woher wissen Sie, ob eine Ebene senkrecht zu einer anderen steht?
Nachdem wir die Definition senkrechter Ebenen kennengelernt haben, sehen wir uns an, wie man erkennt, ob zwei Ebenen senkrecht zueinander stehen oder nicht:
Zwei Ebenen sind senkrecht, wenn ihre Normalenvektoren senkrecht zueinander stehen. Um festzustellen, ob zwei Ebenen senkrecht zueinander stehen, müssen wir daher den Winkel berechnen, den ihre Normalenvektoren bilden. Wenn diese einen Winkel von 90° bilden, bedeutet dies, dass die Ebenen senkrecht zueinander stehen.
Um die Rechtwinkligkeit zweier Ebenen zu ermitteln, müssen Sie also wissen , wie der Winkel zwischen zwei Vektoren berechnet wird . Wenn Sie nicht wissen, wie es geht, können Sie den Link konsultieren. Dort finden Sie unsere Erklärung sowie die notwendige Formel zur Bestimmung des Winkels zwischen zwei Vektoren. Darüber hinaus haben Sie die Möglichkeit, Beispiele zu sehen und mit gelösten Übungen zu üben.
Aber kurz gesagt: Zwei Vektoren stehen senkrecht zueinander, wenn ihr Skalarprodukt Null ist. Daher stehen zwei Ebenen senkrecht zueinander, wenn das Skalarprodukt ihrer zugehörigen Normalenvektoren 0 ist.
Beispiel für zwei senkrechte Ebenen
Überprüfen wir zum Beispiel, ob die folgenden zwei Ebenen senkrecht zueinander stehen:
![]()
![]()
Die Koordinaten X, Y, Z des Vektors normal zu einer Ebene stimmen mit den Koeffizienten A, B, C seiner allgemeinen (oder impliziten) Gleichung überein. Daher ist der Normalenvektor zu jeder Ebene:
![]()
![]()
Und jetzt überprüfen wir, ob es sich um zwei senkrechte Ebenen handelt, indem wir das Skalarprodukt zwischen ihren Normalenvektoren berechnen:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{n}_1 \cdot \vv{n}_2 & = (3,-4,2)\cdot (2,5,7) \\[2ex] & = 3 \cdot 2 +(-4) \cdot 5 +2 \cdot 7 \\[2ex] &=6-20+14 \\[2ex] &\bm{= 0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-94cfcef6a93720224eff0bd4891839ed_l3.png)
Das Skalarprodukt zwischen den beiden Normalenvektoren ist 0, die beiden Ebenen stehen also senkrecht zueinander.
Berechnen Sie eine Ebene senkrecht zu einer Geraden in einem Punkt
Ein typisches Ebenen- und Linienproblem besteht darin, die Gleichung einer Ebene senkrecht zu einer Linie an einem bestimmten Punkt zu finden. Als nächstes sehen wir uns anhand eines Beispiels an, wie es gelöst wird:
- Finden Sie die Gleichung der Ebene senkrecht zur Linie.

Um
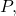
klar und deutlich gesagt:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=-1+4t \\[1.7ex] z=1+t \end{cases} \qquad \qquad P(1,3,-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ac7260ee9792daec4f32e1f200df01b_l3.png)
Zuerst müssen wir den Vektor finden, der normal zur betreffenden Ebene ist. und mag die gerade Linie
![]()
senkrecht zur Ebene steht, fällt ihr Normalenvektor mit dem Richtungsvektor der Geraden zusammen.
In diesem Fall die Linie
![]()
liegt in Form parametrischer Gleichungen vor, daher sind die Komponenten seines Richtungsvektors die Terme vor dem Parameter
![]()
![]()
Somit ist der Vektor normal zur Ebene derselbe wie der Richtungsvektor der Linie:
![]()
Und daher lautet die implizite (oder allgemeine) Gleichung des Plans wie folgt:
![]()
Es reicht also aus, den Wert des Koeffizienten D zu bestimmen. Dazu setzen wir in seine Gleichung die Koordinaten des Punktes ein, dessen Aussage uns sagt, dass er zur Ebene gehört:
![]()
![]()
![]()
![]()
![]()
Kurz gesagt lautet die kartesische Gleichung der Ebene:
![]()
Wenn Sie hingegen weitere Übungen zur Rechtwinkligkeit zwischen geometrischen Objekten üben möchten, können Sie unsere Seite über senkrechte Linien besuchen. Sie finden alles, was Sie über senkrechte Linien wissen müssen: wann zwei Linien senkrecht zueinander stehen, wie man eine senkrechte Linie zueinander berechnet, Beispiele, gelöste Übungen und vieles mehr.
Eigenschaften senkrechter Ebenen
Alle senkrechten Ebenen haben die folgenden Eigenschaften:
- Symmetrische Beziehung : Wenn eine Ebene senkrecht zu einer anderen Ebene steht, steht diese Ebene auch senkrecht zur ersten Ebene. Diese Eigenschaft besitzen auch parallele Ebenen.
![]()
- Nichtreflexive Eigenschaft : Offensichtlich kann keine Ebene senkrecht zu sich selbst sein.
![]()
- Satz: Im dreidimensionalen (3D) Raum muss jedes Ebenenpaar senkrecht zu einer dritten Ebene notwendigerweise parallel sein. Mit anderen Worten: Wenn eine Ebene senkrecht zu einer anderen Ebene steht und diese Ebene auch senkrecht zu einer dritten Ebene steht, sind die erste und die letzte Ebene parallel zueinander.