Seitliche grenzen

In diesem Artikel erklären wir, was der laterale Grenzwert einer Funktion ist (mit Beispielen). Außerdem zeigen wir Ihnen, wie Sie die linken und rechten seitlichen Grenzen einer Funktion sowohl grafisch als auch numerisch berechnen. Darüber hinaus können Sie mit Übungen trainieren, die Schritt für Schritt an den seitlichen Grenzen gelöst werden.

Was sind die seitlichen Grenzen?

Laterale Grenzen einer Funktion an einem Punkt untersuchen das Verhalten der Funktion um diesen Punkt herum. Es gibt die linke seitliche Grenze und die rechte seitliche Grenze, die den Wert der Funktion links bzw. rechts vom betrachteten Punkt analysieren.

Seitliche Begrenzungen links und rechts

Wie wir bei der Definition von Seitengrenzen gesehen haben, gibt es zwei Arten: linke Seitengrenzen und rechte Seitengrenzen.

Der linke Grenzwert der Funktion wird durch ein Minuszeichen an der Stelle ausgedrückt, an der der Grenzwert analysiert wird, und der rechte Grenzwert wird dagegen durch das Pluszeichen angezeigt.

Sehen Sie sich das folgende Beispiel an, um die Bedeutung seitlicher Grenzen besser zu verstehen:

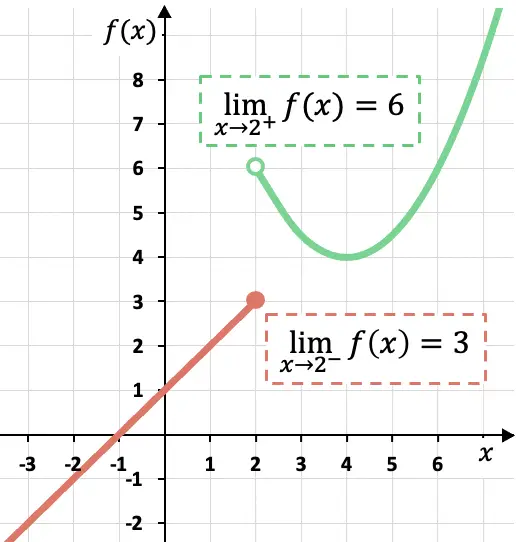
Wie Sie in der grafischen Darstellung dieser stückweisen Funktion sehen können, hängen die seitlichen Grenzen von der Seite ab, auf der sie berechnet werden.

In diesem Fall nähert sich die Funktion 3, wenn x sich von links 2 nähert, da die Funktion Werte annimmt, die näher an 3 liegen, wenn x sich von links x=2 nähert.

Andererseits ist die seitliche Grenze der Funktion bei x=2 durch die Linie 6 wert. Denn wenn wir uns dem Punkt x=2 durch seine Linie nähern, nimmt die Funktion Werte an, die immer näher an f(x)= liegen 6.

Andererseits sollten Sie wissen, dass seitliche Begrenzungen dieselben Eigenschaften haben wie gewöhnliche Begrenzungen. Im folgenden Link können Sie die Grenzeigenschaften sehen:

➤ Siehe: Grenzeigenschaften

gleiche seitliche Grenzen

Wir haben gerade ein Beispiel gesehen, bei dem die Seitengrenzen einer Funktion unterschiedlich sind, aber… was passiert, wenn die Seitengrenzen gleich sind?

Wenn beide Seitengrenzen einer Funktion an einem Punkt existieren und gleich sind , existiert der Grenzwert der Funktion an diesem Punkt und das Ergebnis des Grenzwerts ist der Wert der Seitengrenzen.

Mit anderen Worten: Damit der Grenzwert einer Funktion an einem Punkt existiert, muss die folgende Bedingung erfüllt sein:

Wenn also die seitlichen Grenzen einer Funktion an einem Punkt unterschiedlich sind, existiert der Grenzwert der Funktion an diesem Punkt nicht.

Außerdem ist die Existenz des Grenzwerts einer Funktion an einem Punkt eine wesentliche Voraussetzung dafür, dass es sich um eine stetige Funktion an einem Punkt handelt.

Lassen Sie uns ein Beispiel lösen, um das Konzept der seitlichen Grenzen vollständig zu verstehen:

Die seitlichen Grenzen am Punkt x=-2 der grafisch dargestellten Funktion fallen zusammen, da der Wert der Funktion gegen 3 tendiert, unabhängig davon, ob wir uns x=-2 von links oder von rechts nähern. Daher ist der Grenzwert der Funktion bei x=-2 gleich 3.

Andererseits sind am Punkt x=4 die seitlichen Grenzen unterschiedlich, da sich die Funktion von links an f(x)=3 annähert, von rechts jedoch an f(x)=2. Der Grenzwert der Funktion an dieser Stelle existiert daher nicht.

Berechnung seitlicher Grenzen

Angesichts der Definition der seitlichen Grenzen werden wir sehen, wie sie numerisch berechnet werden, indem wir das folgende Beispiel lösen:

Wenn wir den Grenzwert wie üblich berechnen, erhalten wir die Unbestimmtheit einer reellen Zahl dividiert durch 0:

Bei der Berechnung der seitlichen Grenzen erhalten wir jedoch keine Unbestimmtheit.

Um die seitliche Grenze der Funktion von links bei x=2 zu berechnen, müssen Sie eine Zahl kleiner als x=2, aber sehr nahe daran nehmen, zum Beispiel x=1,999.

In diesem Fall ist der Nenner eine negative Zahl mit einem sehr kleinen Wert, aber nicht einmal Null, und wird normalerweise durch eine Null und ein Minuszeichen davor dargestellt:

Daher ist das Ergebnis der seitlichen Grenze minus Unendlich, da jede Zahl geteilt durch 0 Unendlich ergibt und positiv geteilt durch negativ negativ ergibt:

Wir können überprüfen, ob sich die Funktion minus unendlich nähert, indem wir Bilder der Funktion mit Werten berechnen, die von links näher an x=2 liegen.

Um den Grenzwert der Funktion am Punkt x=2 auf der rechten Seite zu finden, können wir die gleiche Überlegung anwenden: Wir nehmen einen Wert an, der größer als 2 ist, aber sehr nahe beieinander liegt, wie 2001.

Auf die gleiche Weise können wir überprüfen, ob die Funktion gegen Unendlich tendiert, indem wir Bilder der Funktion mit Werten berechnen, die von rechts immer näher an x=2 liegen.

In der folgenden Grafik sehen Sie die analysierte Funktion dargestellt. Wie Sie sehen können, ist die seitliche Grenze der Funktion am Punkt x=2 links minus Unendlich und die seitliche Grenze der Funktion am Punkt x=2 rechts ist plus Unendlich.

Probleme mit seitlichen Begrenzungen behoben

Übung 1

Finden Sie die seitlichen Grenzen der folgenden stückweise definierten Funktion an den Punkten, an denen sich die Definition ändert (x=-2 und x=4).

Die seitlichen Grenzen fallen im Punkt x=-2 nicht zusammen, links tendiert die Funktion zu f(x)=5 und rechts ist die Funktion dagegen konstant und hat den Wert 3.

Auch die Seitengrenzen unterscheiden sich, wenn x sich 4 nähert. Die stückweise Funktion nähert sich von links 3, von rechts jedoch -2.

Übung 2

Bestimmen Sie, ob der Grenzwert existiert, wenn x sich 3 der folgenden stückweisen Funktion nähert, und wenn ja, welchen Wert hat er?

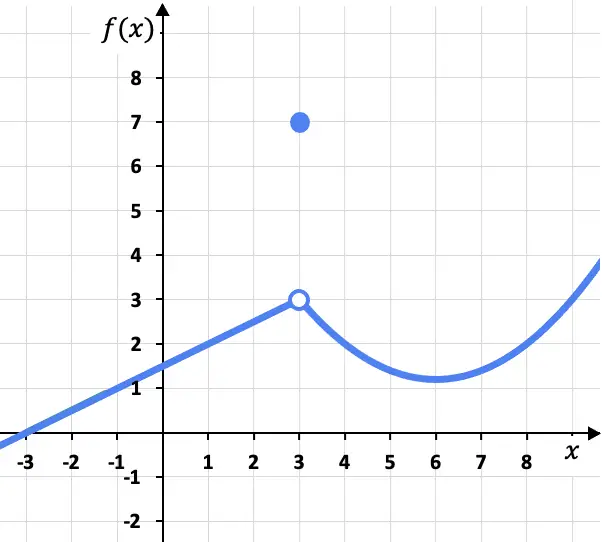
Bei diesem Problem sind die seitlichen Grenzen am Punkt x=3 von links und von rechts identisch, da die Funktion unabhängig davon, ob sie von links oder von rechts angefahren wird, zum gleichen Wert (f(x)=3) tendiert . seine rechte Seite:

Daher ist gemäß der mathematischen Definition des Grenzwerts der Grenzwert der Funktion, wenn x gegen 3 tendiert, gleich 3, da die beiden seitlichen Grenzwerte an demselben Punkt bei diesem Wert zusammenfallen:

Obwohl der Grenzwert der Funktion bei x=3 3 ist, muss berücksichtigt werden, dass die Funktion an diesem Punkt nicht 3 ist, sondern dass f(3)=7 ist. Wie wir später sehen werden, bedeutet dies, dass die Funktion bei x=3 nicht stetig ist, sondern eine vermeidbare Diskontinuität aufweist.

Übung 3

Berechnen Sie die seitlichen Grenzen der folgenden rationalen Funktion am Punkt x=4.

Um den Grenzwert zu berechnen, wenn x von links nach 4 tendiert, nehmen wir einen Wert kleiner als 4, aber sehr nahe daran, zum Beispiel 3.999:

Wenn sich x von links 4 nähert, beträgt die seitliche Grenze also plus Unendlich.

Und um den Grenzwert zu lösen, wenn x von rechts in Richtung 4 tendiert, bewerten wir die Funktion bei einem Wert größer als 4, aber sehr nahe daran, zum Beispiel 4.001:

Wenn sich x von rechts der Zahl 4 nähert, ist die seitliche Grenze also minus unendlich.

Übung 4

Finden Sie den Grenzwert (falls vorhanden) der folgenden stückweisen Funktion, die am Punkt x=2 definiert ist: