▷ Schräge Asymptote einer Funktion (gelöste Aufgaben)

In diesem Artikel erklären wir, was die schrägen Asymptoten einer Funktion sind. Sie erfahren, wann eine Funktion eine schiefe Asymptote hat und wie diese berechnet wird. Darüber hinaus können Sie Beispiele für schräge Asymptoten sehen und mit Übungen üben, die Schritt für Schritt gelöst werden.

Was ist eine schräge Asymptote?

Die schiefe Asymptote einer Funktion ist eine geneigte Linie, der sich ihr Graph auf unbestimmte Zeit nähert, ohne sie jemals zu kreuzen. Folglich sind alle schrägen Asymptoten Geraden mit der Gleichung y=mx+n .

Steigung und Ursprung einer schrägen Asymptote werden mit den folgenden Formeln berechnet:

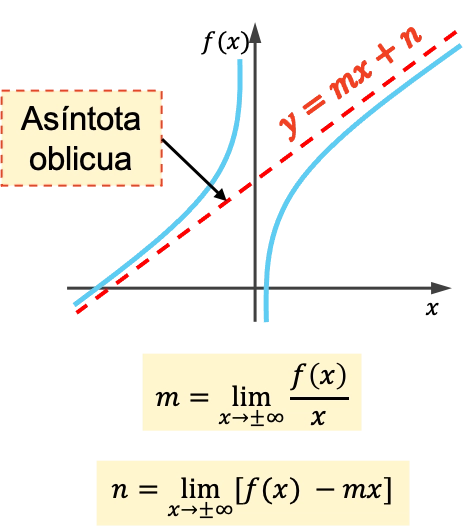
So berechnen Sie die schräge Asymptote einer Funktion

Um die schräge Asymptote einer Funktion zu berechnen, müssen folgende Schritte durchgeführt werden:

Berechnen Sie den Grenzwert der durch x dividierten Funktion bis ins Unendliche.
Wenn der obige Grenzwert zu einer reellen Zahl ungleich Null führt, bedeutet dies, dass die Funktion eine schiefe Asymptote hat. Darüber hinaus ist die Steigung dieser schrägen Asymptote der am Grenzwert erhaltene Wert.

$\displaystyle m = \lim_{x \to \pm\infty}\frac{f(x)}{x}$

In diesem Fall müssen Sie nur noch den Achsenabschnitt der schiefen Asymptote berechnen, indem Sie den folgenden Grenzwert lösen:

$\displaystyle n = \lim_{x \to \pm\infty} [f(x)-mx]$

Hinweis: Die Grenzwerte müssen bei plus und minus unendlich berechnet werden, aber normalerweise liefern sie das gleiche Ergebnis und deshalb vereinfachen wir, indem wir ±∞ einsetzen. Wenn aber die Grenzen bei plus und minus unendlich unterschiedlich wären, müssten die linke schräge Asymptote und die rechte schräge Asymptote getrennt berechnet werden.

Beispiel für eine schräge Asymptote

Als nächstes nehmen wir die schräge Asymptote der folgenden rationalen Funktion, damit Sie ein Beispiel dafür sehen können, wie dies gemacht wird:

$f(x)=\cfrac{x^2+1}{x}$

Die schrägen Asymptoten sind vom Typ

$y=mx+n.$

Also berechnen wir zunächst die Steigung der Geraden

$m$

mit der entsprechenden Formel:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}$

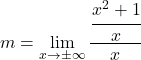
Um diese Grenze aufzulösen, müssen wir die Eigenschaften von Brüchen anwenden:

$\cfrac{\cfrac{a}{b}}{\cfrac{c}{d}}=\cfrac{a\cdot d}{b\cdot c}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}=\lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2}$

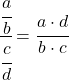
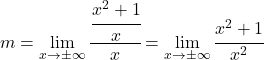
Und jetzt berechnen wir den Grenzwert:

$\displaystyle m = \lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2} = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = \bm{1}$

In diesem Fall ist das Ergebnis der Unbestimmtheit der Unendlichkeit zwischen Unendlichkeit die Division der Koeffizienten von x höchsten Grades, da Zähler und Nenner von gleicher Ordnung sind.

Der obige Grenzwert ergibt eine reelle Zahl ungleich Null, sodass die Funktion eine schräge Asymptote hat. Wir berechnen nun den y-Achsenabschnitt

$n$

der Asymptote unter Verwendung der entsprechenden Formel:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right]$

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-1x\right]$

Wir versuchen den Grenzwert zu berechnen:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Aber wir erhalten die Unbestimmtheit Unendlichkeit minus Unendlich. Daher ist es notwendig, die Begriffe auf einen gemeinsamen Nenner zu bringen. Dazu multiplizieren und dividieren wir x durch den Nenner des Bruchs:

$\displaystyle n=\lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x\cdot x}{x} \right] = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x}\right]$

Da die beiden Begriffe nun denselben Nenner haben, können wir sie gruppieren:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x} \right] = \lim_{x \to \pm\infty} \cfrac{x^2+1-x^2}{x}$

Wir operieren mit dem Zähler:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}$

Und schließlich lösen wir das Limit auf:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}= \cfrac{1}{\pm\infty} = \bm{0}$

Also n =0. Daher ist die schräge Asymptote eine lineare Funktion:

$y = mx+n$

$y = 1x+0$

$\bm{y=x}$

Die untersuchte Funktion ist in der folgenden Grafik dargestellt. Wie Sie sehen, kommt die Funktion der Geraden y=x sehr nahe, berührt sie aber nie, da es sich um eine schräge Asymptote handelt:

Gelöste Übungen zu schrägen Asymptoten

Übung 1

Finden Sie die schräge Asymptote der folgenden rationalen Funktion:

$\displaystyle f(x)= \frac{x^2+2x+3}{x+1}$

Sehen Sie sich die Lösung an

Die schrägen Asymptoten haben die Form

$y=mx+n$

, ist es daher notwendig, die Parameter m und n zu berechnen. Wir berechnen zunächst m , indem wir die Formel anwenden:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+2x+3}{x+1}}{x}$

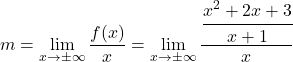
Wir vereinfachen den Bruch, indem wir die Eigenschaften von Brüchen anwenden:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{(x+1)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}$

Und wir lösen das Limit:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}= \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Also m =1. Berechnen wir nun den Achsenabschnitt der schiefen Asymptote, indem wir ihre Formel anwenden:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-1x\right]$

Wir versuchen den Grenzwert zu berechnen:

$\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right]= \bm{+\infty - \infty}$

Aber wir erhalten die unbestimmte Form Unendlichkeit minus Unendlichkeit. Wir müssen daher die Begriffe auf einen gemeinsamen Nenner bringen und sie dann gruppieren:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right] =\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x \cdot (x+1)}{x+1} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x^2+x}{x+1} \right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \frac{x^2+2x+3-(x^2+x)}{x+1}\\[6ex]\displaystyle =\lim_{x \to \pm\infty} \frac{x^2+2x+3-x^2-x}{x+1}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{x+3}{x+1}\end{array}$

Und schließlich lösen wir das Limit auf:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{x+3}{x+1} = \frac{\infty}{\infty} = \frac{1}{1} = \bm{1}$

Kurz gesagt ist die schräge Asymptote der Funktion:

$y = mx+n$

$y = 1x + 1$

$\bm{y = x + 1}$

Übung 2

Finden Sie alle schrägen Asymptoten der folgenden rationalen Funktion:

$\displaystyle f(x)=\frac{2x^2-5}{x+3}$

Sehen Sie sich die Lösung an

Zunächst verwenden wir die Formel für die Steigung der schrägen Asymptote:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{2x^2-5}{x+3}}{x}$

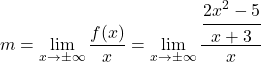
Wir vereinfachen den Bruch, indem wir die Eigenschaften von Brüchen anwenden:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{(x+3)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}$

Und wir bestimmen die Grenze:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}= \frac{+\infty}{+\infty} = \frac{2}{1} = \bm{2}$

Der Grenzwert gibt eine reelle Zahl ungleich Null an, es handelt sich also um eine rationale Funktion mit einer schiefen Asymptote, deren Steigung 2 ist.

Berechnen wir nun den Achsenabschnitt, indem wir die entsprechende Formel anwenden:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]$

Wir versuchen den Grenzwert zu berechnen:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]= \bm{+\infty - \infty}$

Aber wir erhalten die Differenzunbestimmtheit von Unendlichkeiten. Deshalb bringen wir die Terme auf einen gemeinsamen Nenner und rechnen dann:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-\frac{2x\cdot (x+3)}{x+3} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{2x^2-5}{x+3}-\frac{2x^2+6x}{x+3}\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty}\frac{2x^2-5-(2x^2+6x)}{x+3}\\[6ex]\displaystyle =\lim_{x \to \pm\infty}\frac{2x^2-5-2x^2-6x}{x+3}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{-6x-5}{x+3}\end{array}$

Und schließlich lösen wir das Limit auf:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{-6x-5}{x+3}= \frac{\infty}{\infty}=\frac{-6}{1} = \bm{-6}$

Zusammenfassend ist die schräge Asymptote der Bruchfunktion:

$y = mx+n$

$\bm{y=2x-6}$

Schräge asymptote

Was ist eine schräge Asymptote?

So berechnen Sie die schräge Asymptote einer Funktion

Beispiel für eine schräge Asymptote

Gelöste Übungen zu schrägen Asymptoten

Übung 1

Übung 2

Kommentar verfassen Kommentieren abbrechen