In diesem Artikel finden Sie die Definition des Weierstrass-Theorems. Darüber hinaus können Sie anhand mehrerer Schritt-für-Schritt-Übungen den Satz von Weierstraß lösen, um ihn perfekt zu verstehen.
Aussage zum Satz von Weierstrass
Der Satz von Weierstrass besagt, dass eine Funktion, die in einem geschlossenen Intervall stetig ist, in diesem Intervall ein absolutes Maximum und ein absolutes Minimum hat.
➤ Siehe: Was ist eine stetige Funktion?
Der Satz von Weierstrass besagt nur, dass es ein Maximum und ein Minimum gibt, es ist jedoch nicht sinnvoll, die Werte dieser Punkte zu berechnen.
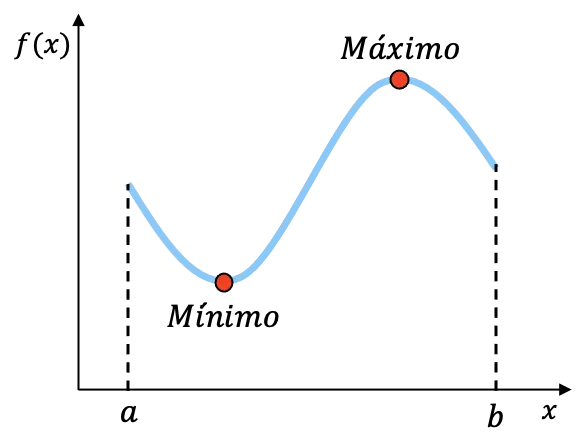
Beispielsweise ist die oben dargestellte Funktion im Intervall [a,b] stetig und weist in diesem Intervall ein Minimum und ein Maximum auf. Obwohl wir die genauen Koordinaten dieser beiden Punkte nicht kennen können, wissen wir, dass die Funktion diese beiden Endpunkte im Intervall hat.
➤ Siehe: So berechnen Sie das Maximum und Minimum einer Funktion
Da die Funktion über das gesamte Intervall stetig ist, bedeutet dies, dass sie im selben Intervall auch alle möglichen Werte zwischen dem absoluten Minimum und dem absoluten Maximum annimmt.
Darüber hinaus kann man als Konsequenz aus dem Weierstrass-Theorem ableiten, dass jede stetige Funktion in einem geschlossenen Intervall nach oben und unten begrenzt ist und die Ober- und Untergrenze der Funktion das absolute Maximum bzw. Minimum sind.
Mathematisch lässt sich der Satz von Weierstrass wie folgt ausdrücken:
Gold
Und
sind zwei eingeschlossene Punkte (das absolute Minimum bzw. das absolute Maximum) im geschlossenen Intervall
![[a,b]](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png "Rendered by QuickLaTeX.com")
in dem die Funktion definiert ist.
Der Beweis des Satzes von Weierstrass ist ziemlich kompliziert und trägt nicht viel zum Konzept bei, daher werden wir ihn in diesem Artikel nicht erklären. Wichtig ist, dass Sie verstehen, was der Satz von Weierstrass ist und wofür er verwendet wird.
Der Weierstrass-Satz löste Probleme
Übung 1
Bestimmen Sie, ob die folgende Funktion auf das vorgeschlagene Intervall beschränkt ist:
![f(x)=\log_3(x-4) \qquad x \in [5,10]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e6a705ea1c5d586cf31d683ac7ccc85_l3.png "Rendered by QuickLaTeX.com")
➤ Siehe: Definitionsbereich einer logarithmischen Funktion
Wir können feststellen, ob die Funktion auf das Intervall [5,10] beschränkt ist, indem wir den Satz von Weierstrass anwenden. Wir müssen daher wissen, ob die Funktion in diesem Intervall stetig ist. Dazu berechnen wir den Definitionsbereich der logarithmischen Funktion:
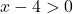
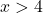
Die Funktion ist für alle Werte größer als x=4 stetig, also im Intervall [5,10].
Daher erfüllt die Funktion den Satz von Weierstrass für das Intervall [5,10], was bedeutet, dass sie in diesem Intervall nach oben und unten beschränkt ist.
Übung 2
Bestimmen Sie, ob die folgende Funktion im vorgeschlagenen Intervall ein Maximum und/oder Minimum aufweist:
![f(x)=\cfrac{3x^2-4}{2x-4} \qquad x \in [-3,3]](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f2e72f629bae2c39821ddbfbf6c93fc_l3.png "Rendered by QuickLaTeX.com")
➤ Siehe: Bereich einer rationalen Funktion
Zunächst analysieren wir die Stetigkeit der rationalen Funktion:
Allerdings weist die Funktion bei x=2 eine Diskontinuität auf, was bedeutet, dass sie im Intervall [-3,3] nicht stetig ist.
Kurz gesagt, die Funktion erfüllt nicht den Satz von Weierstrass und daher können wir nicht sagen, ob sie in diesem Intervall ein Minimum oder Maximum hat.
Übung 3
Bestimmen Sie, ob die folgende Funktion im vorgeschlagenen Intervall ein Maximum und/oder Minimum aufweist, und berechnen Sie diese Punkte:
![f(x)=x^2+3 \qquad x \in [0,4]](https://mathority.org/wp-content/ql-cache/quicklatex.com-4dd0cf4151f8b5c1b4e69be89b7a71e1_l3.png "Rendered by QuickLaTeX.com")
➤ Siehe: Eigenschaften quadratischer Funktionen
Der Definitionsbereich jeder quadratischen Funktion sind alle reellen Zahlen:
Die Funktion ist daher im Intervall [0,4] stetig und erfüllt den Satz von Weierstrass. Die Funktion hat daher in diesem Intervall ein absolutes Minimum und ein absolutes Maximum.
Darüber hinaus liegt der Scheitelpunkt dieser Parabel genau bei x=0, sodass die Funktion im Intervall [0,4] streng ansteigend ist und folglich das Minimum bei x=0 und das Maximum bei x=4 liegt.
Karl Weierstraß
Nachdem wir gesehen haben, was der Satz von Weierstrass bedeutet, werden wir kurz erklären, wer das Inventar dieses Satzes war.
Karl Theodor Wilhelm Weierstrass war ein sehr bedeutender deutscher Mathematiker des 19. Jahrhunderts, genauer gesagt, er wurde am 31. Oktober 1815 in Ostenfelde geboren und starb am 19. Februar 1897 in Berlin.
Neben dem Weierstrass-Theorem ist er auch für seine anderen Beiträge zur Mathematik bekannt. Darunter definierte er Stetigkeit, Grenzwert und Ableitung, drei sehr wichtige Funktionskonzepte.
Ebenso gelang es ihm, bestimmte Sätze zu demonstrieren, die zu diesem Zeitpunkt noch nicht mathematisch verifiziert waren, wie etwa den Satz von Bolzano-Weierstraß, den Mittelwertsatz oder den Satz von Heine-Borel.
Als Kuriosität gibt es zu seinen Ehren einen Mondkrater und einen Asteroiden, die nach Weierstrass benannt wurden.