Auf dieser Seite erfahren Sie, was der Satz von Rouché Frobenius ist und wie man damit den Rang einer Matrix berechnet. Außerdem finden Sie Beispiele und Übungen, die Schritt für Schritt mit dem Rouché-Frobenius-Theorem gelöst werden.
Was ist das Rouché-Frobenius-Theorem?
Das Rouché-Frobenius-Theorem ist eine Methode zur Klassifizierung linearer Gleichungssysteme. Mit anderen Worten: Der Satz von Rouché-Frobenius wird verwendet, um herauszufinden, wie viele Lösungen ein Gleichungssystem hat, ohne es lösen zu müssen.
Es gibt 3 Arten von Gleichungssystemen:
- Systemkompatibel bestimmt (SCD): Das System verfügt über eine einzigartige Lösung.
- Unbestimmtes kompatibles System (ICS): Das System hat unendlich viele Lösungen.
- Systeminkompatibel (SI): Das System hat keine Lösung.
Darüber hinaus wird uns der Satz von Rouché-Frobenius später auch ermöglichen , Systeme mithilfe der Cramer-Regel zu lösen .
Aussage des Rouché-Frobenius-Theorems
Das besagt das Rouché-Frobenius-Theorem
ist die Matrix, die durch die Koeffizienten der Unbekannten eines Gleichungssystems gebildet wird. und der Bauch
oder erweiterte Matrix ist die Matrix, die aus den Koeffizienten der Unbekannten eines Gleichungssystems und den unabhängigen Termen gebildet wird:
Das Rouché-Frobenius-Theorem ermöglicht es uns, anhand des Rangs der Matrizen A und A‘ zu erkennen, mit welcher Art von Gleichungssystem wir es zu tun haben:
- Wenn Rang(A) = Rang(A‘) = Anzahl der Unbekannten ⟶ Ermitteltes kompatibles System (SCD)
- Wenn Rang(A) = Rang(A‘) < Anzahl der Unbekannten ⟶ Unbestimmtes kompatibles System (SCI)
- wenn Bereich(A)
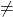
Bereich (A‘) ⟶ Inkompatibles System (SI)
Sobald wir wissen, was der Satz von Rouché-Frobenius sagt, werden wir sehen, wie wir die Übungen zum Satz von Rouché-Frobenius lösen können. Hier sind 3 Beispiele: eine Übung, die mit dem Satz jedes Gleichungssystemtyps gelöst wird.
Beispiel für ein ermitteltes kompatibles System (SCD)
![\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6b2f93c6308c25e8df2fbb5da2af9a8_l3.png "Rendered by QuickLaTeX.com")
Die Matrix A und die erweiterte Matrix A‘ des Systems sind:
![\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-4597f5171b586bbcf0915d8512f7b89d_l3.png "Rendered by QuickLaTeX.com")
Wir berechnen nun den Rang der Matrix A. Dazu prüfen wir, ob die Determinante der gesamten Matrix von 0 verschieden ist:
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c95b7158a2e6401cd16aeb708f128ff_l3.png "Rendered by QuickLaTeX.com")
Da die Matrix eine von 0 verschiedene 3×3-Determinante hat, hat die Matrix A Rang 3:
Sobald wir den Rang von A kennen, berechnen wir den Rang von A‘, der mindestens Rang 3 sein wird, weil wir gerade gesehen haben, dass er eine von 0 verschiedene Determinante der Ordnung 3 enthält. Außerdem kann er nicht den Rang 4 haben. da wir keine Determinante der Ordnung 4 machen können. Daher hat die Matrix A‘ auch den Rang 3:
Da also der Rang der Matrix A gleich dem Rang der Matrix A‘ und der Anzahl der Unbekannten des Systems (3) ist, wissen wir durch den Satz von Rouché Frobenius, dass es sich um ein kompatibles determiniertes System (SCD) handelt. :
![\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png "Rendered by QuickLaTeX.com")
Beispiel eines unbestimmten kompatiblen Systems (ICS)
![\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2360b9a47257f73cf3f5dea63fb24098_l3.png "Rendered by QuickLaTeX.com")
Die Matrix A und die erweiterte Matrix A‘ des Systems sind:
![\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b281235e2702433b447e2586ae3092c9_l3.png "Rendered by QuickLaTeX.com")
Wir berechnen nun den Rang der Matrix A. Dazu prüfen wir, ob die Determinante der gesamten Matrix von 0 verschieden ist:
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-74cafc27ab41134696c3bf263132b98b_l3.png "Rendered by QuickLaTeX.com")
Die Determinante der gesamten Matrix A ergibt 0, hat also nicht den Rang 3. Um zu sehen, ob sie den Rang 2 hat, müssen wir in A eine Untermatrix finden, deren Determinante von 0 verschieden ist. Zum Beispiel die aus der oberen linken Ecke :
![\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-22b2487f7664a70c116593120de2743b_l3.png "Rendered by QuickLaTeX.com")
Da die Matrix eine von 0 verschiedene 2×2-Determinante hat, hat die Matrix A Rang 2:
Sobald wir den Rang von A kennen, berechnen wir den Rang von A‘. Wir wissen bereits, dass die Determinante der ersten drei Spalten 0 ergibt, also probieren wir die anderen möglichen 3×3-Determinanten aus:
![\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-17f264ad3859da88ffa6784be24e4143_l3.png "Rendered by QuickLaTeX.com")
Alle 3×3 Determinanten der Matrix A‘ sind 0, daher wird die Matrix A‘ auch nicht den Rang 3 haben. Im Inneren gibt es jedoch Determinanten der Ordnung 2, die von 0 verschieden sind. Zum Beispiel:
Die Matrix A‘ hat also den Rang 2 :
Die Ausdehnung der Matrix A ist gleich der Ausdehnung der Matrix A‘, diese sind jedoch kleiner als die Anzahl der Unbekannten des Systems (3). Daher handelt es sich nach dem Rouché-Frobenius-Theorem um ein unbestimmtes kompatibles System (ICS):
![\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png "Rendered by QuickLaTeX.com")
Beispiel für ein inkompatibles System (IS)
![\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-30e1084dd637eb4371f6b2218af24136_l3.png "Rendered by QuickLaTeX.com")
Die Matrix A und die erweiterte Matrix A‘ des Systems sind:
![\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b435d86f1466af5748d91e6c9bd813e3_l3.png "Rendered by QuickLaTeX.com")
Wir berechnen nun den Rang der Matrix A. Dazu prüfen wir, ob die Determinante der gesamten Matrix von 0 verschieden ist:
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-714538c91aa2620a6adb40581245f0e0_l3.png "Rendered by QuickLaTeX.com")
Die Determinante der gesamten Matrix A ergibt 0, hat also nicht den Rang 3. Um zu sehen, ob sie den Rang 2 hat, müssen wir in A eine Untermatrix finden, deren Determinante von 0 verschieden ist. Zum Beispiel die aus der oberen linken Ecke :
![\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-5a46decda8fd850d9c847922b0c896db_l3.png "Rendered by QuickLaTeX.com")
Da die Matrix eine von 0 verschiedene Determinante der Ordnung 2 hat, hat die Matrix A den Rang 2:
Sobald wir den Rang von A kennen, berechnen wir den Rang von A‘. Wir wissen bereits, dass die Determinante der ersten 3 Spalten 0 ergibt, also versuchen wir es jetzt beispielsweise mit der Determinante der letzten 3 Spalten:
![\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-47aecdf801b92f21f2287fb96eaaa3f8_l3.png "Rendered by QuickLaTeX.com")
Andererseits enthält die Matrix A‘ eine Determinante, deren Ergebnis von 0 verschieden ist, daher hat die Matrix A‘ den Rang 3 :
Da der Rang der Matrix A kleiner ist als der Rang der Matrix A‘, schließen wir aus dem Rouché-Frobenius-Theorem, dass es sich um ein inkompatibles System (SI) handelt :
![\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3da0513f318d25473e93ba88c51fb42_l3.png "Rendered by QuickLaTeX.com")
Probleme des Rouché-Frobenius-Theorems gelöst
Übung 1
Bestimmen Sie den Typ des folgenden Gleichungssystems mit 3 Unbekannten mithilfe des Satzes von Rouché-Frobenius:
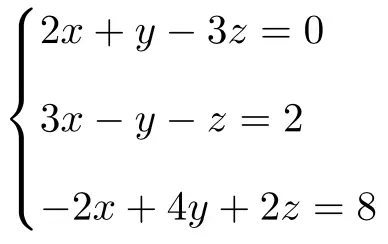
Wir erstellen zunächst die Matrix A und die erweiterte Matrix A‘ des Systems:
![\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-951ce5c1f0c606d4f060a1de58b60303_l3.png "Rendered by QuickLaTeX.com")
Wir müssen nun den Rang der Matrix A ermitteln. Dazu prüfen wir, ob die Determinante der Matrix von 0 verschieden ist:
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-15cddb69f7590648d1d6ae61d942471e_l3.png "Rendered by QuickLaTeX.com")
Die Matrix hat eine von 0 verschiedene Determinante dritter Ordnung, die Matrix A hat Rang 3:
Sobald wir den Rang von A kennen, berechnen wir den Rang von A‘. Dies wird mindestens Rang 3 sein, da wir gerade gesehen haben, dass es eine von 0 verschiedene Determinante der Ordnung 3 enthält. Darüber hinaus kann es nicht Rang 4 sein, da wir keine 4×4-Determinante erstellen können. Daher hat die Matrix A‘ auch den Rang 3:
Dank des Rouché-Frobenius-Theorems wissen wir also, dass es sich um ein determiniertes kompatibles System (SCD) handelt, da der Bereich von A gleich dem Bereich von A‘ und der Anzahl der Unbekannten ist.
![\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png "Rendered by QuickLaTeX.com")
Übung 2
Klassifizieren Sie das folgende Gleichungssystem mit 3 Unbekannten mithilfe des Rouché-Frobenius-Theorems:
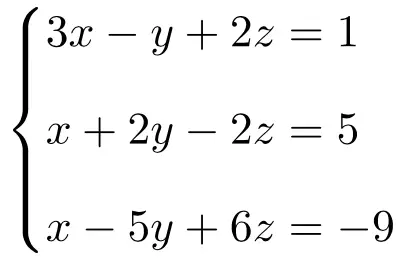
Wir konstruieren zunächst die Matrix A und die erweiterte Matrix A‘ des Systems:
![\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-45e13aabe233ece927df7c9ba0bb3ec1_l3.png "Rendered by QuickLaTeX.com")
Berechnen wir nun den Bereich der Matrix A:
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-87bc95df0033834bba0398b8421faac5_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-b9805283b75e2b89f67c7865a1263112_l3.png "Rendered by QuickLaTeX.com")
Matrix A hat also Rang 2:
Sobald wir den Rang von A kennen, berechnen wir den Rang von A‘. Wir wissen bereits, dass die Determinante der ersten drei Spalten 0 ergibt, also probieren wir die anderen möglichen 3×3-Determinanten aus:
![\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-e6457fe3f03722b7f0d955191f318915_l3.png "Rendered by QuickLaTeX.com")
Alle 3×3 Determinanten der Matrix A‘ sind 0, daher wird die Matrix A‘ auch nicht den Rang 3 haben. Im Inneren gibt es jedoch viele Determinanten der Ordnung 2, die sich von 0 unterscheiden. Zum Beispiel:
![\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-eafa4747802fae3f0c36350357abbeb2_l3.png "Rendered by QuickLaTeX.com")
Die Matrix A‘ hat also den Rang 2 :
Der Rang der Matrix A ist gleich dem Rang der Matrix A‘, aber diese beiden sind kleiner als die Anzahl der Unbekannten des Systems (3). Daher wissen wir durch das Rouché-Frobenius-Theorem, dass es sich um ein unbestimmtes kompatibles System (ICS) handelt:
Übung 3
Bestimmen Sie mithilfe des Rouché-Frobenius-Theorems, um welche Art von System es sich bei dem folgenden Gleichungssystem handelt:
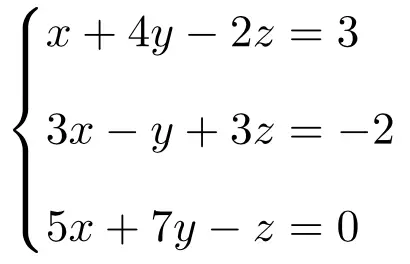
Wir erstellen zunächst die Matrix A und die erweiterte Matrix A‘ des Systems:
![\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1820d31e4fd5c79804c9b6fa15abb469_l3.png "Rendered by QuickLaTeX.com")
Berechnen wir nun den Bereich der Matrix A:
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-4f998260ee4c96673085ea6fd4ca87ba_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-159a1c58fdcd972b4b08e4795950e064_l3.png "Rendered by QuickLaTeX.com")
Matrix A hat also Rang 2:
Sobald wir den Rang von A kennen, berechnen wir den Rang von A‘. Wir wissen bereits, dass die Determinante der ersten 3 Spalten 0 ergibt, die Determinante der letzten 3 Spalten jedoch nicht:
![\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c673a5bbbd41933208169fa3e08b7c62_l3.png "Rendered by QuickLaTeX.com")
Daher hat die Matrix A‘ Rang 3 :
Der Rang der Matrix A ist kleiner als der Rang der Matrix A‘, daher können wir aus dem Rouché-Frobenius-Theorem ableiten, dass es sich um ein inkompatibles System (SI) handelt :
Übung 4
Bestimmen Sie den Typ des folgenden Gleichungssystems mit 3 Unbekannten mithilfe des Satzes von Rouché-Frobenius:
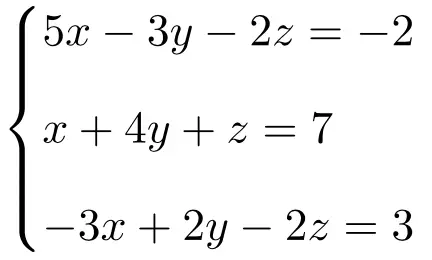
Wir erstellen zunächst die Matrix A und die erweiterte Matrix A‘ des Systems:
![\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8a0454c53a64f612c689ba1dae1196b_l3.png "Rendered by QuickLaTeX.com")
Wir müssen nun den Rang der Matrix A berechnen. Dazu lösen wir die Determinante der Matrix mit der Sarrus-Regel:
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-420f0d1ee000f39cbfbce88bf122f413_l3.png "Rendered by QuickLaTeX.com")
Die Matrix hat eine von 0 verschiedene Determinante dritter Ordnung, die Matrix A hat Rang 3:
Daher hat die Matrix A‘ auch den Rang 3 , da sie immer mindestens den Rang A hat, und sie kann nicht den Rang 4 haben, da wir keine 4×4-Determinante auflösen können.
Dank der Anwendung des Rouché-Frobenius-Theorems wissen wir also, dass das System ein kompatibles determiniertes System (SCD) ist, da der Bereich von A gleich dem Bereich von A‘ und der Anzahl der Unbekannten ist.
Übung 5
Identifizieren Sie mithilfe des Rouché-Frobenius-Theorems, um welche Art von System es sich bei dem folgenden Gleichungssystem handelt:
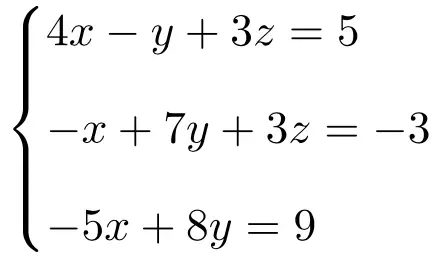
Wir erstellen zunächst die Matrix A und die erweiterte Matrix A‘ des Systems:
![\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3211e276b2b040969c38bc6c69eabd52_l3.png "Rendered by QuickLaTeX.com")
Berechnen wir nun den Bereich der Matrix A:
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-21004095a3a8ef3edfc15bed5c7853a4_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a58059046b56cf1f8d82c6c8939e44ca_l3.png "Rendered by QuickLaTeX.com")
Matrix A hat daher Rang 2:
Sobald wir den Rang von A kennen, berechnen wir den Rang von A‘. Die Determinante der ersten drei Spalten, die wir bereits kennen, ergibt 0, aber die Determinante der letzten drei Spalten ergibt nicht:
![\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-992718d3b50aedf77c80c262fad5845f_l3.png "Rendered by QuickLaTeX.com")
Daher hat die Matrix A‘ Rang 3 :
Und schließlich wenden wir den Bereich auf das Rouché-Frobenius-Theorem an: Der Bereich der Matrix A ist kleiner als der Bereich der Matrix A‘, es handelt sich daher um ein inkompatibles System (SI) :
Übung 6
Klassifizieren Sie das folgende Gleichungssystem der Ordnung 3 mit dem Satz von Rouché-Frobenius:
![\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d45e8bc425b08e403a98e01693201681_l3.png "Rendered by QuickLaTeX.com")
Wir konstruieren zunächst die Matrix A und die erweiterte Matrix A‘ des Systems:
![\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e779eca9135adc44e4a3a55f368560f_l3.png "Rendered by QuickLaTeX.com")
Berechnen wir nun den Bereich der Matrix A:
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2f63f79858eae462547cf2f270fc780_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5fa293b94b8c6acfd998f1e154abf7a_l3.png "Rendered by QuickLaTeX.com")
Matrix A hat also Rang 2:
Sobald wir den Rang von A kennen, berechnen wir den Rang von A‘. Wir wissen bereits, dass die Determinante der ersten drei Spalten 0 ergibt, also probieren wir die anderen möglichen 3×3-Determinanten aus:
![\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-98958f866454a1bf9f1ac078562065cd_l3.png "Rendered by QuickLaTeX.com")
Alle 3×3 Determinanten der Matrix A‘ sind 0, daher wird die Matrix A‘ auch nicht den Rang 3 haben. Im Inneren gibt es jedoch Determinanten der Ordnung 2, die sich von 0 unterscheiden. Zum Beispiel:
![\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-58091f1a37a4ef81fdf56f01dd9531a3_l3.png "Rendered by QuickLaTeX.com")
Die Matrix A‘ hat also den Rang 2 :
Schließlich wissen wir durch die Anwendung des Rouché-Frobenius-Theorems, dass es sich um ein unbestimmtes kompatibles System (ICS) handelt, da der Bereich der Matrix A gleich dem Bereich der Matrix A‘ ist, diese beiden jedoch kleiner sind als die Anzahl der Unbekannten im System(3):
