Relative Positionen einer Linie und einer Ebene

Auf dieser Seite finden Sie die relativen Positionen einer Linie und einer Ebene. Wir erklären Ihnen, wie die relative Lage zwischen einer Geraden und einer Ebene berechnet wird (2 Methoden) und können zusätzlich Beispiele und Übungen Schritt für Schritt gelöst sehen.

Was sind die relativen Positionen zwischen einer Linie und einer Ebene?

Bevor wir uns alle möglichen relativen Positionen zwischen einer Linie und einer Ebene ansehen, müssen wir natürlich wissen , was Linien und was eine Ebene sind . Wenn Ihnen diese beiden Konzepte also immer noch nicht ganz klar sind, empfehlen wir Ihnen, zunächst einen Blick auf die verlinkten Seiten zu werfen, auf denen sie ausführlich erklärt werden.

Daher gibt es in der analytischen Geometrie nur drei relative Positionen im Raum zwischen einer Linie und einer Ebene:

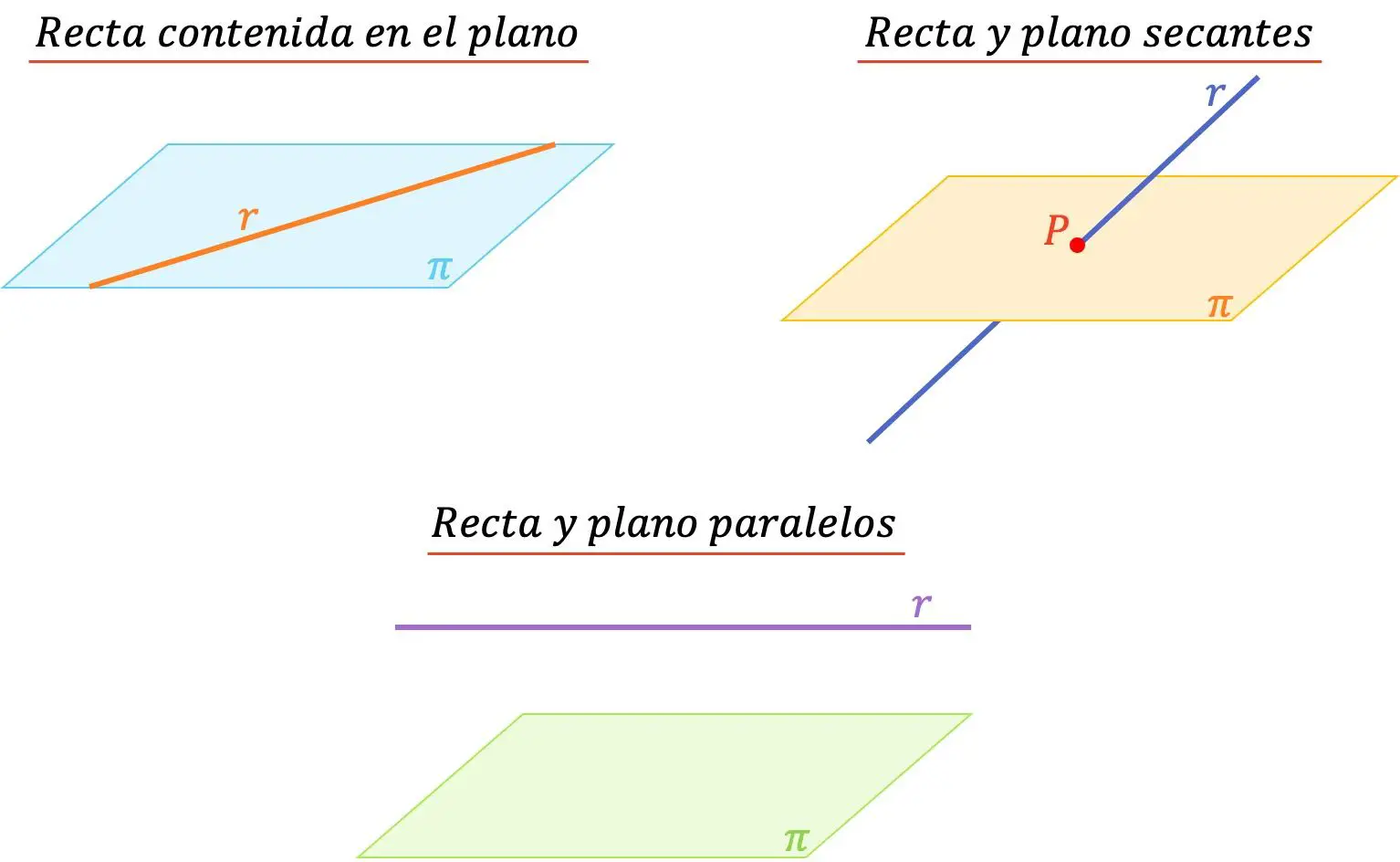
In der Ebene enthaltene Linie : Wenn die Linie in der Ebene enthalten ist, bedeutet dies, dass sie unendlich viele gemeinsame Punkte haben.
Parallele Linie und Ebene : Eine Linie und eine Ebene sind parallel, wenn sie keinen gemeinsamen Punkt haben.
Schnittlinie und Ebene : Eine Linie und eine Ebene schneiden sich, wenn die Linie die Ebene in einem Punkt schneidet. Sie haben also nur eines gemeinsam.

Wenn die Linie hingegen in der Ebene liegt oder parallel zueinander ist, beträgt der Winkel, den sie bilden, 0°. Wenn sich hingegen die Linie und die Ebene schneiden, kann der Winkel zwischen den beiden geometrischen Elementen zwischen 0° (nicht eingeschlossen) und 90° (einschließlich) liegen.

Wie berechnet man die relative Position einer Linie und einer Ebene?

Es gibt hauptsächlich zwei Methoden, um die relative Position zwischen einer Linie und einer Ebene im Raum zu ermitteln: anhand von Bereichen oder anhand von Vektoren .

Wenn die Gerade als implizite (oder allgemeine) Gleichung ausgedrückt wird, ist es einfacher, die Rangmethode zu verwenden. Wenn die Gerade hingegen durch einen anderen Gleichungstyp angegeben wird, beispielsweise wenn sie in Form eines Vektors, einer parametrischen oder kontinuierlichen Gleichung vorliegt, ist es schneller, die Vektormethode zu verwenden.

Wenn Sie sich nicht erinnern, wie die Gleichungen der Linie aussehen, hinterlassen wir Ihnen eine Seite, auf der Sie alle Gleichungen der Linie einsehen können. Hier finden Sie alle Gleichungen der Geraden, eine Formel zum schnellen Finden der Gleichung einer Geraden durch zwei Punkte, Beispiele und Schritt für Schritt gelöste Übungen.

Daher ist es praktischer, je nach Problem die eine oder andere Methode zu verwenden. Aus diesem Grund empfehlen wir Ihnen, zu wissen, wie beide Verfahren durchgeführt werden. Nachfolgend finden Sie die Erläuterung beider Methoden anhand von Beispielen.

Wenn die Gerade die Form einer impliziten (oder allgemeinen) Gleichung hat

Eine Möglichkeit, die relative Position zwischen einer Linie und einer Ebene zu bestimmen, besteht darin, den Rang zweier Matrizen zu berechnen.

Wenn die Gerade durch ihre impliziten (oder allgemeinen) Gleichungen definiert ist:

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0\end{cases}$

Und der Plan wird auch in Form einer allgemeinen Gleichung ausgedrückt:

$\pi : \ A_3x+B_3y+C_3z+D_3=0$

Wir nennen A die Matrix, die aus den Koeffizienten A, B und C der Gleichungen der Ebene und der Geraden besteht:

$\displaystyle A =\begin{pmatrix} A_1&B_1&C_1\\[1.1ex] A_2&B_2&C_2\\[1.1ex] A_3&B_3&C_3\end{pmatrix}$

Und die Matrix A‘ ist die erweiterte Matrix mit allen Koeffizienten der beiden Gleichungen:

$\displaystyle A' =\begin{pmatrix} A_1&B_1&C_1&D_1\\[1.1ex] A_2&B_2&C_2&D_2\\[1.1ex] A_3&B_3&C_3&D_3\end{pmatrix}$

Dann wird die relative Position zwischen der Linie und der Ebene durch den Wert der Ausdehnung der beiden vorherigen Matrizen gemäß der folgenden Tabelle bestimmt:

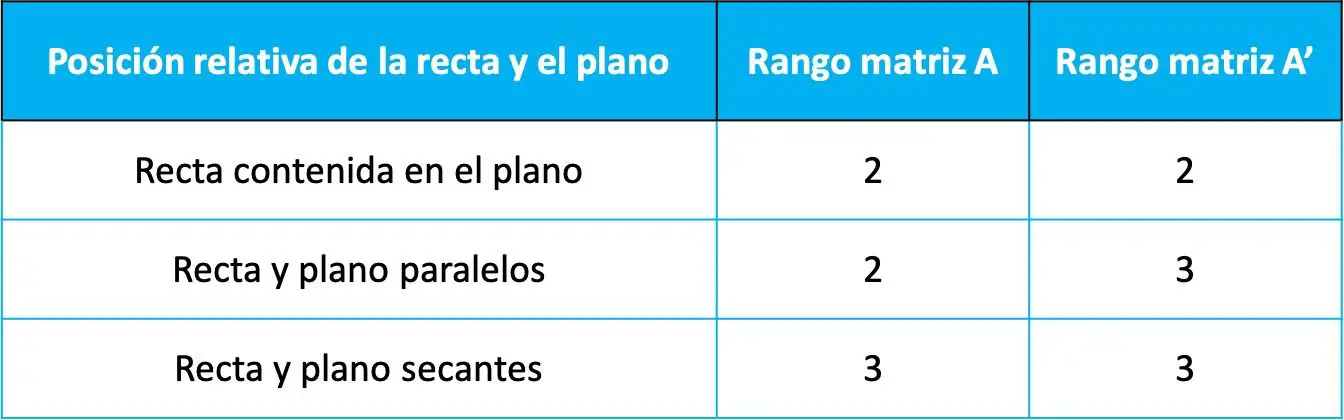
Untersuchen Sie die relative Position zwischen einer Linie und einer Ebene im Raum anhand von Bereichen

Dass die relativen Positionen von den Rängen dieser beiden Matrizen abhängen, kann anhand des Rouche-Frobenius-Toerems (ein Satz zur Lösung linearer Gleichungssysteme) gezeigt werden. Auf dieser Seite werden wir die Demonstration jedoch nicht durchführen, da es nicht erforderlich ist, sie zu kennen, und sie auch nicht viel bringt.

Beispiel dafür, wie man die relative Position einer Linie und einer Ebene anhand von Bereichen ermittelt

Damit Sie genau sehen können, wie das geht, lösen wir beispielhaft eine Übung:

Untersuchen Sie die relative Position zwischen der folgenden Linie und der folgenden Ebene:

$\displaystyle r: \ \begin{cases}2x+y+z+3=0 \\[2ex] 4x-y+5z+2=0\end{cases}$

$\pi : \ 2x+2y-6=0$

Die Linie wird durch zwei sich schneidende Ebenen definiert, das heißt, sie wird als implizite Gleichung ausgedrückt. Daher verwenden wir die Rangmethode, um die relative Position zwischen der Linie und der Ebene zu untersuchen.

Als erstes müssen Sie die Matrix A und die erweiterte Matrix A‘ mit den Koeffizienten der Gleichungen konstruieren:

$\displaystyle A =\begin{pmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&1&1&3\\[1.1ex] 4&-1&5&2\\[1.1ex] 2&2&0&-6\end{pmatrix}$

Und jetzt müssen wir den Rang jeder Matrix berechnen. Wir ermitteln zunächst den Umfang der Matrix A anhand von Determinanten:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1\\[1.1ex] 4&-1\end{vmatrix} =-6 \neq 0$

$rg(A) = 2$

Die Determinante der Matrix A ist Null, sie enthält jedoch eine 2×2-Untermatrix, deren Determinante von Null verschieden ist, es handelt sich also um eine Matrix vom Rang 2.

Andererseits ist es auch notwendig, den Rang der Matrix A‘ zu berechnen. Und der Bereich der erweiterten Matrix A‘ wird immer mindestens derselbe sein wie der der Matrix A, wir müssen also nur prüfen, ob sie den Rang 3 oder 2 hat:

$rg(A') = \ ?$

$\displaystyle \begin{vmatrix} 2&1&3\\[1.1ex] 4&-1&2\\[1.1ex] 2&2&-6\end{vmatrix} =62 \neq 0$

$rg(A') = 3$

Andererseits hat die erweiterte Matrix A‘ eine von 0 verschiedene 3×3-Unterdeterminante, sie hat daher den Rang 3.

Da also Matrix A den Rang 2 und Matrix A‘ den Rang 3 hat, sind die Linie und die Ebene parallel .

Wenn die Gerade die Form einer anderen Art von Gleichung hat

Wenn die Linie durch eine andere als die implizite Gleichung ausgedrückt wird, sei es eine Vektor-, eine parametrische oder eine kontinuierliche Gleichung, ist es vorzuziehen, die unten erläuterte Methode zu verwenden.

Wenn die Gerade also in Form einer Vektorgleichung, parametrischer Gleichungen oder einer kontinuierlichen Gleichung vorliegt, bedeutet das, dass wir einen Punkt kennen, der zur Geraden gehört, und auch seinen Richtungsvektor.

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r \\[2ex] P\end{cases}$

Andererseits wissen wir auch, wie der Normalvektor (oder Senkrechtvektor) zur Ebene lautet:

$\vv{n} \perp \pi$

Aus den beiden Vektoren und dem Punkt der Geraden lässt sich dann die relative Lage zwischen der Geraden und der Ebene wie folgt berechnen:

Wenn das Skalarprodukt zwischen dem Richtungsvektor der Geraden und dem Normalenvektor zur Ebene ungleich Null ist, bedeutet dies, dass die Gerade eine Sekante zur Ebene ist.

$\vv{\text{v}}_r\cdot \vv{n} \neq 0 \ \color{orange}\longrightarrow \color{black} \ \text{recta y plano secantes}$
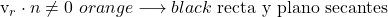
Wenn aber das Skalarprodukt zwischen dem Richtungsvektor der Linie und dem Normalenvektor zur Ebene gleich Null ist, gibt es zwei Möglichkeiten: Die Linie liegt in der Ebene oder sie sind parallel. Und um zu wissen, um welchen Fall es sich handelt, müssen wir die Koordinaten eines Punktes auf der Geraden in die Gleichung der Ebene einsetzen.
- Wenn der Punkt die Gleichung der Ebene erfüllt, ist die Linie in der Ebene enthalten.
- Wenn andererseits der Punkt die Gleichung der Ebene nicht erfüllt, sind die Linie und die Ebene parallel.

Beispiel für die Bestimmung der relativen Lage einer Linie und einer Ebene mithilfe von Vektoren

Nachdem wir die Theorie dieser Methode kennengelernt haben, sehen wir uns nun eine Übung an, die Schritt für Schritt gelöst wird:

Finden Sie die relative Position zwischen der folgenden Linie und der folgenden Ebene:

$\displaystyle r: \ \begin{cases}x=2-3t \\[1.7ex] y=-1+2t \\[1.7ex] z=-2t\end{cases}$

$\pi : \ 2x+y-2z-3=0$

Zunächst wird die Linie als parametrische Gleichung definiert, sodass ihr Richtungsvektor und ein Punkt, durch den sie verläuft, lauten:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(-3,2,-2) \\[2ex] P(2,-1,0) \end{cases}$

Und andererseits ist der Vektor normal zur Ebene:

$\vv{n} =(2,1,-2)$

Sobald wir den Richtungsvektor der Linie und den Normalenvektor zur Ebene kennen, müssen wir das Skalarprodukt zwischen beiden berechnen:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (-3,2,-2) \cdot (2,1,-2) \\[2ex] & = -3 \cdot 2+2 \cdot 1 -2\cdot (-2) \\[2ex] &= -6 +2 +4 \\[2ex] & = 0\end{aligned}$

Das Ergebnis des Skalarprodukts ist Null, die Gerade kann also nur in der Ebene enthalten oder parallel zu dieser sein. Um herauszufinden, um welchen Fall es sich handelt, setzen wir die kartesischen Koordinaten des Punktes auf der Geraden in die Gleichung der Ebene ein:

$2x+y-2z-3=0 \ \xrightarrow{P(2,-1,0)} \ 2\cdot 2 -1 -2 \cdot 0 -3 = 0$

$4- 1 -0 -3 = 0$

$0 = 0$

Indem wir den Punkt der Linie in die Gleichung der Ebene einsetzen, erhalten wir eine Gleichheit, d. h. der Punkt respektiert die Gleichung der Ebene und folglich ist die Linie in der Ebene enthalten .

Relative positionen einer linie und einer ebene