Auf dieser Seite werden die unterschiedlichen relativen Positionen zwischen einer Linie und einem Kreis erläutert. Darüber hinaus erfahren Sie, wie Sie die relative Position zwischen einer Linie und einem Kreis ermitteln.
Was sind die relativen Positionen einer Linie und eines Kreises?
In der analytischen Geometrie kann die relative Position einer Linie in Bezug auf einen Kreis nur Äußerlichkeit, Tangente oder Sekante sein:
- Außen : wenn der Abstand zwischen der Linie und dem Mittelpunkt des Kreises größer als der Radius ist.
- Tangente : wenn der Abstand zwischen der Linie und dem Mittelpunkt des Kreises gleich dem Radius ist.
- Sekante : wenn der Abstand zwischen der Linie und dem Mittelpunkt des Kreises kleiner als der Radius ist.
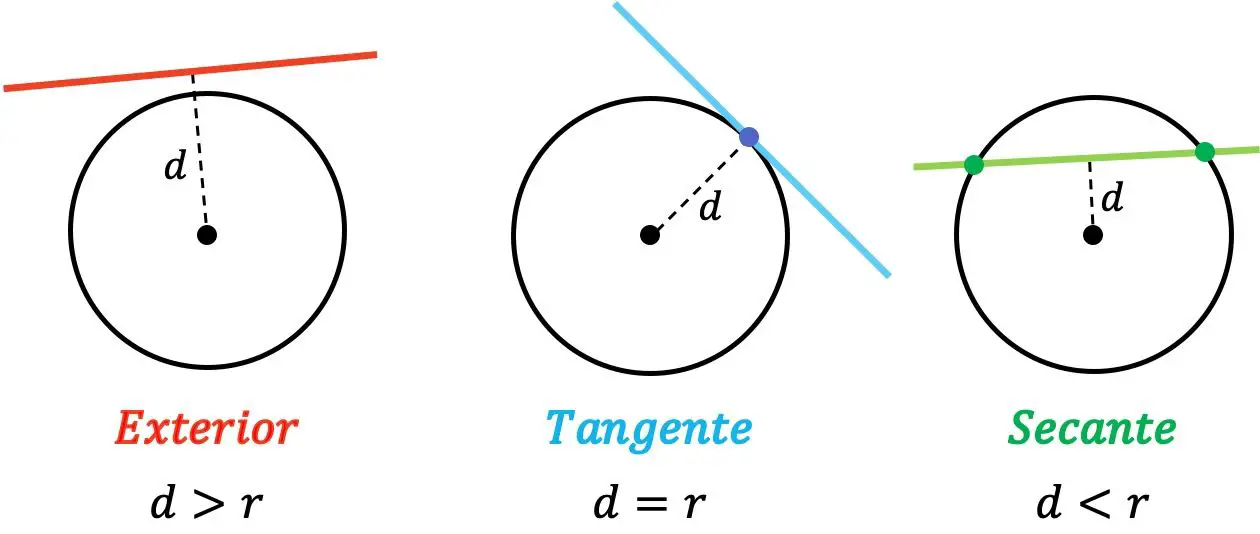
Liegt also eine Gerade außerhalb eines Kreises, schneidet sie diesen an keinem Punkt. Wenn andererseits die Linie den Kreis tangiert, haben beide einen gemeinsamen Punkt. Und schließlich ist eine Gerade eine Sekante eines Kreises, wenn sie ihn an zwei verschiedenen Punkten schneidet.
Wie bestimmt man die relative Position zwischen einer Linie und einem Kreis?
Es gibt zwei Möglichkeiten, die relative Position einer Linie in Bezug auf einen Kreis in der Ebene zu ermitteln: eine durch Berechnen des Abstands zwischen der Linie und dem Mittelpunkt des Kreises und die andere durch Lösen eines zusammengesetzten Gleichungssystems der Gleichung von die Gerade und die Kreisgleichung.
Als nächstes sehen wir uns genau an, was jede Methode ist.
Methode 1: Abstand zwischen der Linie und dem Mittelpunkt des Kreises
Wie wir bei der Erklärung des Konzepts der relativen Position zwischen einer Linie und einem Kreis gesehen haben, gibt der Abstand zwischen einer Linie und dem Mittelpunkt eines Kreises an, um welche Art von relativer Position es sich handelt.
Diese Methode besteht also darin, den Abstand zwischen der Linie und dem Mittelpunkt des Kreises zu ermitteln. Um dies tun zu können, müssen Sie natürlich wissen , wie man den Abstand zwischen einem Punkt und einer Linie berechnet . Auf dieser Seite können Sie sehen, wie das geht, sowie Beispiele und gelöste Übungen zum Üben.
Abhängig vom Ergebnis der erhaltenen Distanz wird es also der eine oder andere Fall sein:
- Die Linie liegt außerhalb des Kreises, wenn der ermittelte Abstand größer als der Kreisradius ist.
- Die Linie ist tangential zum Kreis, wenn der erhaltene Abstand dem Radius des Kreises entspricht.
- Die Linie schneidet den Kreis, wenn der erhaltene Abstand kleiner als der Radius des Kreises ist.
Methode 2: Lösen Sie ein Gleichungssystem
Eine andere Möglichkeit, die relative Position einer Linie zu einem Kreis zu ermitteln, besteht darin, ein Gleichungssystem zu verwenden, das aus der Liniengleichung und der Kreisgleichung besteht. Um diese Methode anwenden zu können, müssen Sie natürlich wissen , wie die Gleichung des Umfangs lautet und wie die Formel für die Gleichung der Linie lautet.
Abhängig von der Anzahl der Lösungen des Gleichungssystems werden wir mit dem einen oder anderen Fall konfrontiert:
- Wenn das Gleichungssystem keine Lösung hat, bedeutet das, dass die Gerade und der Kreis keinen gemeinsamen Punkt haben, die Gerade also außerhalb des Kreises liegt.
- Wenn das Gleichungssystem eine Lösung hat, bedeutet dies, dass die Gerade und der Kreis einen gemeinsamen Punkt haben, die Gerade also den Kreis tangiert .
- Wenn das Gleichungssystem zwei Lösungen hat, bedeutet dies, dass die Gerade und der Kreis zwei gemeinsame Punkte haben, die Gerade also eine Sekante zum Kreis ist.