Auf dieser Seite finden Sie die Erklärung der verschiedenen Methoden, die es gibt, um die relative Position zweier Geraden in der Ebene (im R2) zu bestimmen. Darüber hinaus sehen Sie mehrere Beispiele und können anhand von Schritt für Schritt gelösten Übungen üben.
Wie ist die relative Lage zweier Geraden in der Ebene?
Bevor Sie sich die relativen Positionen zwischen zwei Linien in der Ebene ansehen, müssen Sie natürlich genau wissen, was eine Linie ist. Sie können es in der Definition von Linie finden.
Beim Arbeiten in zwei Dimensionen (in R2) gibt es also drei Arten möglicher relativer Positionen zwischen zwei Linien:
Schnittlinien

Zwei sich schneidende Geraden haben nur einen gemeinsamen Punkt.
Parallele Linien

Zwei Geraden sind parallel, wenn sie keinen gemeinsamen Punkt haben. Das heißt, wenn sich ihre Wege nie kreuzen.
zusammenfallende Linien

Zwei Geraden sind gleich, wenn alle ihre Punkte gemeinsam sind.
Andererseits hängt der Winkel zwischen zwei Geraden in der Ebene auch von ihrer relativen Lage ab:
- Schnittlinien schneiden sich in einem Winkel zwischen 0° (nicht eingeschlossen) und 90° (einschließlich). Wenn sie außerdem nur einen rechten Winkel von 90° bilden, bedeutet das, dass die beiden Linien senkrecht zueinander stehen.
- Parallele Linien bilden einen Winkel von 0°, da sie die gleiche Richtung haben.
- Und aus dem gleichen Grund bilden die zusammenfallenden Linien auch einen Winkel von 0° zwischen sich.
Wenn Sie wissen möchten, wie der Winkel zwischen zwei Linien berechnet wird, können Sie sich die Formel für den Winkel zwischen zwei Linien ansehen. Hier finden Sie eine ausführliche Erklärung zur Bestimmung des Winkels zwischen zwei Linien sowie mehrere Beispiele und sogar gelöste Übungen, damit Sie das Konzept üben und vollständig verstehen können.
So ermitteln Sie die relative Position zweier Linien in der Ebene
Die Kenntnis der relativen Position zwischen zwei Linien im zweidimensionalen Raum hängt davon ab, wie die Linien ausgedrückt werden:
- Linienrichtungsvektoren: Wenn zwei Linien einen unterschiedlichen Richtungsvektor haben, müssen sie sich schneiden. Wenn andererseits die Koordinaten ihrer Richtungsvektoren gleich oder proportional sind, können sie parallel sein oder zusammenfallen (es muss überprüft werden, ob sie einen gemeinsamen Punkt haben).
- Explizite Gleichung: wenn zwei Geraden unterschiedliche Steigungen haben
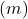
Sie trocknen im Gegenteil, wenn die Linien die gleiche Steigung, aber eine unterschiedliche Reihenfolge im Ursprung haben
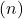
sie sind parallel. Schließlich werden zwei Linien verwechselt, wenn sie ursprünglich gleiche Steigungen und Ordinaten haben.
- Allgemeine (oder implizite) Gleichung: Zwei Geraden mit den nichtproportionalen Koeffizienten A und B schneiden sich immer. Sie sind jedoch parallel, wenn diese beiden Parameter zueinander proportional sind, nicht jedoch zum Koeffizienten C. Und wenn die drei Terme schließlich proportional sind, bedeutet dies, dass die Linien verwechselt sind.
Wenn Sie Zweifel an den Gleichungen der Linie oben haben, können Sie die Erklärung der Gleichungen der Linie in der Ebene konsultieren. Hier finden Sie die Formel aller Geradengleichungen, deren Berechnung, Beispiele und gelöste Aufgaben zu Geradengleichungen.
In der folgenden Tabelle finden Sie eine Zusammenfassung der bisherigen Eigenschaften:

Als nächstes sehen wir uns zwei Beispiele an, wie man die relative Position zwischen zwei Linien bestimmt:
Beispiel 1
- Finden Sie die relative Position zwischen den folgenden zwei Linien, die in Form einer expliziten Gleichung definiert sind:
![]()
Die beiden Geraden haben die gleiche Steigung:
![]()
Aber sie haben unterschiedliche Computer im Ursprung:
![]()
Da sie also die gleiche Steigung, aber unterschiedliche Achsenabschnitte haben, sind die Linien parallel .
Beispiel 2
- Bestimmen Sie die relative Position zwischen den folgenden beiden Linien, ausgedrückt durch ihre implizite (oder allgemeine) Gleichung:
![]()
Beide Geraden werden als explizite Gleichung ausgedrückt, daher müssen wir prüfen, ob einer ihrer Koeffizienten proportional ist:
![]()
Die 3 Terme der Linien sind proportional, daher fallen die Linien zusammen .
Bestimmen Sie die relative Lage zweier Geraden in der Ebene mit einem Gleichungssystem
Eine andere Möglichkeit, die relative Position zwischen zwei Linien zu ermitteln, besteht darin, das Gleichungssystem zu analysieren, das aus den Gleichungen der Linien besteht:
- Wenn das System eine eindeutige Lösung hat , schneiden sich die Geraden. Darüber hinaus ist der Schnittpunkt der beiden Geraden die Lösung des Systems.
- Wenn es sich um ein System ohne Lösung handelt, bedeutet dies, dass die Geraden keine gemeinsamen Punkte haben und es sich daher um parallele Geraden handelt.
- Wenn das System unendlich viele Lösungen hat , bedeutet dies, dass die Geraden alle Punkte gemeinsam haben und es sich daher um Schnittlinien handelt.
Beispiel 3
- Berechnen Sie die relative Position der folgenden beiden Linien mithilfe eines Gleichungssystems:
![]()
Um die relative Position der beiden Linien zu ermitteln, müssen wir das folgende lineare Gleichungssystem lösen, das durch die beiden Linien gebildet wird:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-243b1e787e6532fbafbfca53d934f4ad_l3.png)
In diesem Fall lösen wir das System mit der Substitutionsmethode. Wir werden daher die Variable isolieren
![]()
aus der zweiten Gleichung und setze es in die erste Gleichung ein:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\} \begin{array}{l} \\[2ex] \longrightarrow \ y=3-5x \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad3456c92c838f40d60afdb45e1eb2f3_l3.png)
![]()
![]()
![]()
![]()
![]()
Und sobald wir wissen, wie viel das Unbekannte wert ist
![]()
Wir setzen seinen Wert in den gefundenen Ausdruck ein
![]()
![]()
![]()
Wir haben also nur eine Lösung des aus den beiden Geraden zusammengesetzten Gleichungssystems erhalten, die beiden Geraden schneiden sich also. Und der Punkt, an dem sie sich schneiden, ist die Lösung des Systems, also der Punkt
![]()
Probleme der relativen Position zweier Linien in der Ebene gelöst
Übung 1
Bestimmen Sie, ob sich die folgenden Linien schneiden, parallel sind oder zusammenfallen:
![]()
Beide Geraden werden als implizite (oder allgemeine) Gleichung ausgedrückt, daher müssen wir prüfen, ob einer ihrer Koeffizienten proportional ist:
![]()
Nur die Koeffizienten A und B der Geraden sind proportional zueinander und nicht zum Koeffizienten C. Daher sind die beiden Geraden parallel .
Übung 2
Finden Sie die relative Position zwischen den folgenden beiden Linien, ausgedrückt als parametrische Gleichungen:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=4-5t \\[2ex] y= 1+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=-2t \\[2ex] y=6+9t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bafb951a2141722b0bbb7a1681f506ea_l3.png)
Wir könnten das durch die beiden Linien gebildete Gleichungssystem lösen, um ihre relative Position zu ermitteln. Da es sich jedoch um parametrische Gleichungen handelt, kann man ihre Richtungsvektoren leicht ermitteln, und wenn sie nicht proportional sind, bedeutet das, dass sich die Geraden schneiden. Und in diesem Fall werden wir nicht so viel Zeit damit verbringen, ein ganzes Gleichungssystem zu lösen.
Damit sind die kartesischen Koordinaten des Richtungsvektors jeder Linie die Zahlen vor dem Parameter
![]()
![]()
Sobald wir die Richtungsvektoren kennen, überprüfen wir ihre Proportionalität:
![]()
Die Richtungsvektoren sind nicht proportional, daher kreuzen sich die Linien .
Übung 3
Geben Sie an, ob sich die folgenden Linien schneiden, parallel sind oder zusammenfallen, und suchen Sie auch einen Schnittpunkt zwischen ihnen (falls zutreffend).
![]()
Die beiden Geraden werden durch ihre explizite Gleichung definiert und haben unterschiedliche Steigungen:
![]()
Da sie unterschiedliche Steigungen haben, schneiden sich die Linien .
Da sich die Geraden schneiden, haben sie daher einen gemeinsamen Punkt und um ihn zu berechnen, müssen wir das Gleichungssystem lösen, das durch die beiden Geraden gebildet wird:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} y=4x-5\\[2ex] y=-2x+7\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3923ff74a214543ddd2cc44a42e3813_l3.png)
In diesem Fall werden wir das System mit der Ausgleichsmethode lösen, weil beides
![]()
sind bereits gelöscht:
![]()
![]()
![]()
![]()
![]()
Und sobald wir das Unbekannte haben
![]()
Wir ersetzen seinen Wert in jedem Ausdruck von
![]()
um herauszufinden, wie viel es wert ist:
![]()
![]()
Der Schnittpunkt der beiden Geraden ist also das Ergebnis des Systems:
![]()
Übung 4
Berechnen Sie den Wert der Unbekannten
![]()
Und
![]()
sodass die folgenden beiden Geraden parallel sind:
![]()
Die Linien werden in allgemeiner (oder impliziter) Gleichungsform beschrieben. Damit die beiden Geraden parallel sind, müssen ihre Koeffizienten A und B proportional sein, d. h. die folgende Gleichung muss erfüllt sein:
![]()
Wir müssen daher die vorherige Gleichung lösen, um den Wert der Unbekannten zu erhalten
![]()
Dazu multiplizieren wir die Brüche kreuzweise:
![]()
![]()
![]()
Damit die Geraden hingegen parallel sind, können ihre unabhängigen Terme nicht proportional zu den anderen Koeffizienten sein:
![]()
Daher lösen wir die Ungleichung wie zuvor durch Kreuzmultiplikation der Brüche:
![]()
![]()
![]()
Kurz gesagt, damit die beiden Linien parallel sind
![]()
muss 2 sein und
![]()
kann jede reelle Zahl außer 3 sein.
Übung 5
Finden Sie die explizite Gleichung der Geraden parallel zur Geraden
![]()
und was passiert über den Punkt hinweg
![]()
gerade sein
![]()
![]()
Damit die Linie parallel zur Linie ist
![]()
beide müssen die gleiche Steigung haben. und die Steigung der Linie
![]()
ist 2:
![]()
Daher lautet die Gleichung der Geraden, die wir finden müssen:
![]()
Und sobald wir die Steigung der Geraden kennen, können wir den y-Achsenabschnitt berechnen, indem wir den zur Geraden gehörenden Punkt in die Geradengleichung einsetzen:
![]()
![]()
![]()
![]()
![]()
Die explizite Gleichung der Geraden lautet also:
![]()
Wenn Sie es bis hierher geschafft haben, bedeutet das, dass Sie die relativen Positionen zwischen zwei Linien im Plan bereits beherrschen. Gut gemacht!
Viele fragen sich jedoch: Welchen Nutzen hat es, die relative Position zwischen zwei Linien zu kennen?
Nun, eine der Anwendungen der relativen Position zwischen Linien besteht darin, den Abstand zwischen zwei Linien zu ermitteln, da die Berechnung des Abstands zwischen zwei Linien von ihrer relativen Position abhängt:
- Wenn sich die Linien schneiden oder zusammenfallen, ist der Abstand Null.
- Wenn die Linien hingegen parallel sind, muss eine bestimmte Formel angewendet werden. Wenn Sie mehr Interesse haben, können Sie sich ansehen, wie der Abstand zwischen zwei parallelen Linien berechnet wird.